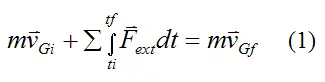
- Momentum is conserved for all types of collisions.
- Two objects collide and separate p1 + p2 = p1 ′ + p2 ′ m1v1 + m2v2 = m1v1 ′ + m2v2 ′
- Two objects collide and stick together p1 + p2 = p1+2 ′ m1v1 + m2v2 = ( m1 + m2) v ′
What is the formula of Conservation of momentum?
- Work out the total momentum before the event (before the collision): p = m × v.
- Work out the total momentum after the event (after the collision): Because momentum is conserved, total momentum afterwards = 60,000 kg m/s.
- Work out the total mass after the event (after the collision):
- Work out the new velocity:
What is the equation used to calculate momentum?
Steps Download Article
- Find the mass. Mass is the amount of matter in an object. To measure the mass of an object, you can use a balance.
- Find the velocity. Velocity is the speed and the direction that the object travels. Right now, we will only concentrate on the speed part.
- Multiply the mass by the velocity. That is the momentum! The measurement for momentum is kg*m/s. ...
How to solve momentum conservation problems?
How to solve conservation of momentum problems.Opens a modal Bouncing fruit collision example Opens a modal Momentum. The law of conservation of momentum can be viewed as a result of Newtons second law of motion F ma and Newtons third law of motion when an object applies a force to a second object the second object applies a force back to the first object that is equal in magnitude and ...
What is the principle of Conservation of linear momentum?
- It’s a conserved quantity whenever the system exhibits translational symmetry.
- Components of linear momentum can be used as canonical coordinates in Hamiltonian mechanics.
- It generates spatial translations: is the operator that shifts a state by .
What are two equations for the conservation of momentum?
SummaryIII1st lawinertia mmomentum p = mv2nd lawforce law F = maimpulse-momentum theorem J = ∆p3rd lawaction-reaction +F1 = −F2conservation of momentum ∑p = ∑p0
What is the momentum principle equation?
p = m v . You can see from the equation that momentum is directly proportional to the object's mass (m) and velocity (v). Therefore, the greater an object's mass or the greater its velocity, the greater its momentum.
What is conservation of momentum and derive its equation?
⇒m1v1+m2v2=m1u1+m2u2. ⇒ Final momentum (pf) = Initial momentum (pi). Thus, we conclude that during the interaction between the two balls, momentum before collision is equal to total momentum after collision. Thus, the momentum of the system is conserved in the absence of external forces.
What is the conservation of momentum example?
The recoil of a Gun: If a bullet is shot from a gun, both the bullet and the gun are at first very still i.e., the total momentum before firing is zero. The bullet gains a forward momentum when it gets discharged. As per the conservation of momentum, the gun gets a regressive momentum.
How do you prove the law of conservation of momentum?
Formula used: p = mv, FAB=−FBA and F=dpdt. Complete answer: Law of conservation of momentum states that unless an external force is applied, the two or more objects acting upon each other in an isolated system, the total momentum of the system remains constant.
What is law of conservation of momentum Class 11?
The principle of conservation of momentum states that if two objects collide, then the total momentum before and after the collision will be the same if there is no external force acting on the colliding objects.
Why is the law of conservation of momentum important class 9?
The importance of this law of conservation of momentum is that as long as no external force acts on a body the velocity vector can be deduced after some period of time of a body if we knew its initial velocity.
What is conservation of linear momentum Class 9?
the law of conservation of linear momentum states that if no external forces act on the system of two colliding objects, then the vector sum of the linear momentum of each body remains constant and is not affected by their mutual interaction.
What does the law of conservation of momentum state?
The law of conservation of momentum states that in an isolated system the total momentum of two or more bodies acting upon each other remains const...
The law of conservation of momentum is based on which law of motion?
The law of conservation of momentum is based on Newton’s third law of motion which states that every force has a reciprocating equal and opposite f...
What is the real-life example of the law of conservation of momentum?
The thrust that you feel at the time of firing is one of the real-life examples of the conservation of momentum.
What is the law of conservation of momentum formula?
The momentum observation principle can be mathematically represented as: m1u1 + m2u2 = m1v1 + m2v2 In the equation, m1 and m2 are masses of the b...
Does friction affect the conservation of momentum?
Yes, friction affects momentum. As friction increases, momentum decreases.
What is the law of conservation of momentum?
The law of conservation of momentum states that if no net external unbalanced force acts on a system, then the total momentum of all the bodies of...
What is momentum?
Momentum of a body is the product of the mass of the body and the velocity of the body.
When is the conservation of momentum applicable?
Conservation of momentum is applicable when there is no net external unbalanced force acting on a system, and the mutual interactions of the bodies...
What is the formula of conservation of momentum?
The formula of conservation of momentum is ({m_A}{v_A} + {m_B}{v_B} = {m_A}{u_A} + {m_B}{u_B}.)
What is the best example of conservation of momentum?
The recoiling of a gun is the best example of conservation of momentum. When the bullet is shot in the forward direction, the gun recoils in the ba...
Which law is the conservation of momentum?
Conservation of momentum is actually a direct consequence of Newton's third law.
What is conservation in physics?
In physics, the term conservation refers to something which doesn't change. This means that the variable in an equation which represents a conserved quantity is constant over time. It has the same value both before and after an event.
Is momentum a vector quantity?
Momentum is a vector quantity, and therefore we need to use vector addition when summing together the momenta of the multiple bodies which make up a system. Consider a system of two similar objects moving away from each other in opposite directions with equal speed. What is interesting is that the oppositely-directed vectors cancel out, so the momentum of the system as a whole is zero, even though both objects are moving.
Is impulse the same as momentum?
If we recall that impulse is equivalent to change in momentum, it follows that the change in momenta of the objects is equal but in the opposite directions. This can be equivalently expressed as the sum of the change in momenta being zero.
How to demonstrate the law of conservation of momentum?
Using motion detectors and carts on a low-friction track, one can collect data to demonstrate the law of conservation of momentum. The video below demonstrates the process.
What is the momentum of an object in a collision?
In a collision, the momentum change of object 1 is equal to and opposite of the momentum change of object 2. That is, the momentum lost by object 1 is equal to the momentum gained by object 2. In most collisions between two objects, one object slows down and loses momentum while the other object speeds up and gains momentum.
How to determine momentum of a brick?
The loaded cart (a cart with a brick on it) is in motion with considerable momentum. The actual momentum of the loaded cart can be determined using the velocity (often determined by a ticker tape analysis) and the mass. The total amount of momentum is the sum of the dropped brick's momentum (0 units) and the loaded cart's momentum . After the collision, the momenta of the two separate objects (dropped brick and loaded cart) can be determined from their measured mass and their velocity (often found from a ticker tape analysis). If momentum is conserved during the collision, then the sum of the dropped brick's and loaded cart's momentum after the collision should be the same as before the collision. The momentum lost by the loaded cart should equal (or approximately equal) the momentum gained by the dropped brick. Momentum data for the interaction between the dropped brick and the loaded cart could be depicted in a table similar to the money table above.
How many units of momentum did the cart lose in the collision?
Note that the loaded cart lost 14 units of momentum and the dropped brick gained 14 units of momentum. Note also that the total momentum of the system (45 units) was the same before the collision as it was after the collision.
How many units of momentum does object 1 lose?
If object 1 loses 75 units of momentum, then object 2 gains 75 units of momentum. Yet, the total momentum of the two objects (object 1 plus object 2) is the same before the collision as it is after the collision. The total momentum of the system (the collection of two objects) is conserved. A useful analogy for understanding momentum conservation ...
What is the most powerful law in physics?
One of the most powerful laws in physics is the law of momentum conservation . The law of momentum conservation can be stated as follows. For a collision occurring between object 1 and object 2 in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision.
How to find the velocity of the Earth?
To find the velocity of the Earth, use the momentum equation, p = m*v. This equation rearranges to v=p/m. By substituting into this equation,
What does Conservation of Momentum Mean?
Conservation of Momentum comes into the picture when bodies interact with each other without any external unbalanced force acting on them. The total momentum of the interacting bodies remains the same before and after the interaction.
How to verify conservation of momentum?
Conservation of Momentum can be verified by considering two bodies that interact with each other without any external unbalanced force acting on them.
Why is momentum important?
It is very important to involve the concept of momentum while discussing the impact of force. For example, the bullet thrown by our hand may not hurt a person, but when the bullet is shot using a gun, it may kill a person. Though the mass of the bullet is the same in both cases, its velocity drastically changes while using it through the gun, and thus its impact on the person gets deadly.
How to find the rate of change of momentum of body A?
So, the rate of change of the momentum of body A is given by m A v A – m A u A t
Which law of motion states that the forces of F A B and F B A are equal in magnitude and opposite in direction?
From Newton’s third law of motion, the forces F A B and F B A are equal in magnitude and opposite in direction to each other.
Is the law of conservation of momentum being verified?
Here, the collision has happened without any external unbalanced force acting on the bodies. Hence, the law of conservation of momentum is being verified.
What is the momentum equation?
Momentum Equation. The momentum equation is a mathematical formulation of the law of conservation of momentum. It states that the rate of change in linear momentum of a volume moving with a fluid is equal to the surface forces and the body forces acting on a fluid.
Who derived the momentum equations and the constitutive equations of the Maxwell liquid for a dynamically loaded?
The momentum equations and the constitutive equations of the Maxwell liquid for a dynamically loaded finite journal bearings are derived by Rastogi et al. [19] and Paranjpe [22]:
How to write velocity distribution?
With y* = y/h and Kn = y/DH = y / (4 h ), the velocity distribution is written as uz = ( U /2) ( y* / (4 Kn (2 – σ )/ σ +1)+1). The centerline velocity is independent of the slip at the walls and the velocity transverse gradient is reduced as rarefaction is increased.
What does the equation of 4.98 represent?
Equation (4.98) represents the momentum production rate due to interaction between different phases along their separating interfaces. It must be specified according to the combination of phases in the multiphase system that is under consideration.
What is Newton's second law of motion?
The momentum equation requires that the time rate of momentum change in a given direction be equal to the sum of the forces acting in that direction. This is known as Newton's second law of motion and in the model used here the forces concerned are gravitational (body) and surface.
How to describe the motion of a group of particles in a fluid?
The motion of a group of particles in a fluid can be described by either the Lagrangian method or the Eulerian method. In the Lagrangian method , the coordinates of the moving particles are represented as functions of time. This means that at some arbitrary time t0, the coordinates of a particle ( x0, y0, z0) are identified and that thereafter we follow that particle through the fluid flow. Thus, the position of the particle at any other instant is given by a set of equations of the form
Why is the Lagrangian approach not used in fluid mechanics?
The Lagrangian approach is not generally used in fluid mechanics because it leads to more cumbersome equations. In the Eulerian method, we observe the flow characteristics in the vicinity of a fixed point as the particles pass by. Thus, in this approach the velocities at various points are expressed as functions of time as
What is momentum conservation?
Momentum Conservation Principle. For two or more bodies in an isolated system acting upon each other, their total momentum remains constant unless an external force is applied. Therefore, momentum can neither be created nor destroyed. The principle of conservation of momentum is a direct consequence of Newton’s third law of motion.
Which law states that a force applied by an object A on an object B exerts back an equal force in magnitude?
Derivation of Conservation of Momentum. Newton’s third law states that for a force applied by an object A on object B, object B exerts back an equal force in magnitude, but opposite in direction. This idea was used by Newton to derive the law of conservation of momentum.
Is momentum a vector quantity?
Momentum is a vector quantity since it has both magnitude and direction.
What is the second law of conservation of momentum?
Newton’s second law of motion says that the rate of change of linear momentum of a body is equal to the net external force applied to it. Mathematically it is expressed as:
Why is momentum conserved?
Since there is no external force acting on the system of two bodies, momentum will be conserved.
What happens to momentum when the net external force is zero?
If the net external force acting on a system of bodies is zero, then the momentum of the system remains constant. We have to remember that the momentum of the system is conserved and not that of the individual particles. The momentum of the individual bodies in the system might increase or decrease according to the situation, ...
What is linear momentum?
The linear momentum of a particle is defined as the product of the mass of the particle times the velocity of that particle. Conservation of momentum of a particle is a property exhibited by any particle where the total amount of momentum never changes. Linear momentum of a particle is a vector quantity and is denoted by.
What does it mean when the rate of change of momentum is zero?
Mathematically it is expressed as: If the net external force acting on a body is zero, then the rate of change of momentum is also zero, which means that there is no change in momentum.
Does momentum increase or decrease?
The momentum of the individual bodies in the system might increase or decrease according to the situation, but the momentum of the system will always be conserved, as long as there is no external net force acting on it.
Why is momentum important?
Momentum is also a really useful concept because it obeys a conservation law, which you've certainly learned in intro physics and which we'll re-derive next. The general idea of a conservation law is simple: if ( C ) is some property of a physical system, then we say that ( C ) is conservedif
What is conservation law?
A conservation law can give us powerful qualitative insights about how different parts of a physical system interact with each other and with the outside world. For example, energy conservation means that there is no such thing as "free energy" - if a black box is producing mechanical energy, it has to be transferred from somewhere!
What is Newton's second law?
Newton's second law tells us that ( vec{F}beta = dvec{p}beta/dt ). As before, our next step is to put together the total momentum of the system,
Which law holds for each of our two masses?
Now, we know that Newton's second law will hold for each of our two masses, so
Can we study projectile motion with quadratic drag?
At this point, the obvious next step would be to try to put our solutions together to study projectile motion with quadratic drag. Unfortunately, there's an obstacle to doing this that wasn't present in the linear case, which we can see if we go back to the vector form of Newton's second law. In the linear case, we have
Can you solve horizontal and vertical motion cases?
which would be required when the Reynolds number is close to 1. It is actually possible to solve the horizontal- and vertical-motion cases analytically here, but those full solutions won't show off anything new and interesting in terms of either physics or math, so we'll skip over them. The full study of projectile motion with both terms can only be done numerically due to the quadratic term.
Does momentum change with net external force?
So we've shown that the total momentum of any collectionof physical objects changes only according to the net externalforce. This is a very powerful result! In particular, momentum conservation will let us make detailed statements about mechanics problems without knowing anything about the (often very complicated!) internal forces at work. Here are a few nice examples, briefly:
What is the analogy of viscous momentum?
In the energy equations, the analogy to viscous momentum transfer is heat transfer through conduction. In fact, in gases, the same mechanism that is responsible for viscosity is also responsible for thermal conductivity and the eddy diffusivity for momentum transfer is also used to compute the eddy diffusivity for heat transfer. Consequently, in cases where we can neglect viscous momentum transfer, we can usually neglect heat transfer through conduction in the energy equations.
How to model multiphase flow?
The most detailed way of modeling multiphase flow is with surface tracking methods, such as the level set or phase field methods. In these models, the interactions between phases — for example, surface tension — are introduced as sources or sinks in the momentum equations at a thin layer with a very small thickness that follows the boundary between the phases. The shape and position of the phase boundary is computed in detail. This means that the momentum and mass conservation equations are combined with a set of transport equations for a level set or phase field function that, at a given value (isosurface), describe the position of the phase boundary.
Who is the inventor of Stokes equations?
The equations are named after the Irish physicist George Gabriel Stokes, who first described viscous momentum transfer through these equations. Which terms to retain from the energy equation depends on the fluid. The convective term can often be neglected, as can pressure-work effects. Viscous heating can also be of interest for Stokes flows in bearings and other lubrication applications, for example.
Is a fluid a continuum?
A flow can be regarded as a continuum flow as long as the Knudsen number is smaller than 10 -3. Liquids can almost always be regarded as continua, as can gases under ordinary circumstances. For gases at very low pressures, or gas flows confined in very small domains, the interaction of the molecules in the fluid may take place with the same frequency as the interaction with the walls that confine the flow. For such systems, the fluid flow has to be described with the rarefied flow equations or at least with Knudsen boundary conditions.
Can we use the equations for the conservation of momentum and mass?
If we can afford to describe a porous structure in detail, with all of its surface structures and surface properties, we can use the equations for the conservation of momentum and mass as usual, defining no-slip conditions on the pore walls or the Knudsen condition if the mean width of the pores is of the same order of magnitude as the scale of molecule interactions.

Conservation
Example
- Consider a collision between two objects - object 1 and object 2. For such a collision, the forces acting between the two objects are equal in magnitude and opposite in direction (Newton's third law). This statement can be expressed in equation form as follows. The above equation is one statement of the law of momentum conservation. In a collision,...
Properties
- The forces act between the two objects for a given amount of time. In some cases, the time is long; in other cases the time is short. Regardless of how long the time is, it can be said that the time that the force acts upon object 1 is equal to the time that the force acts upon object 2. This is merely logical. Forces result from interactions (or contact) between two objects. If object 1 cont…
Resources
- A useful means of depicting the transfer and the conservation of money between Jack and Jill is by means of a table.
Safety
- For any collision occurring in an isolated system, momentum is conserved. The total amount of momentum of the collection of objects in the system is the same before the collision as after the collision. A common physics lab involves the dropping of a brick upon a cart in motion. 1. When fighting fires, a firefighter must use great caution to hold a hose that emits large amounts of wat…
Details
- The dropped brick is at rest and begins with zero momentum. The loaded cart (a cart with a brick on it) is in motion with considerable momentum. The actual momentum of the loaded cart can be determined using the velocity (often determined by a ticker tape analysis) and the mass. The total amount of momentum is the sum of the dropped brick's momentum (0 units) and the loaded car…
Introduction
- Collisions commonly occur in contact sports (such as football) and racket and bat sports (such as baseball, golf, tennis, etc.). Consider a collision in football between a fullback and a linebacker during a goal-line stand. The fullback plunges across the goal line and collides in midair with the linebacker. The linebacker and fullback hold each other and travel together after the collision. Th…
Usage
- Momentum is conserved for any interaction between two objects occurring in an isolated system. This conservation of momentum can be observed by a total system momentum analysis or by a momentum change analysis. Useful means of representing such analyses include a momentum table and a vector diagram. Later in Lesson 2, we will use the momentum conservation principle …
Causes
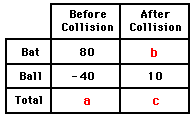
- 9. A Tomahawk cruise missile is launched from the barrel of a mobile missile launcher. Neglect friction. Express your understanding of momentum conservation by filling in the tables below.