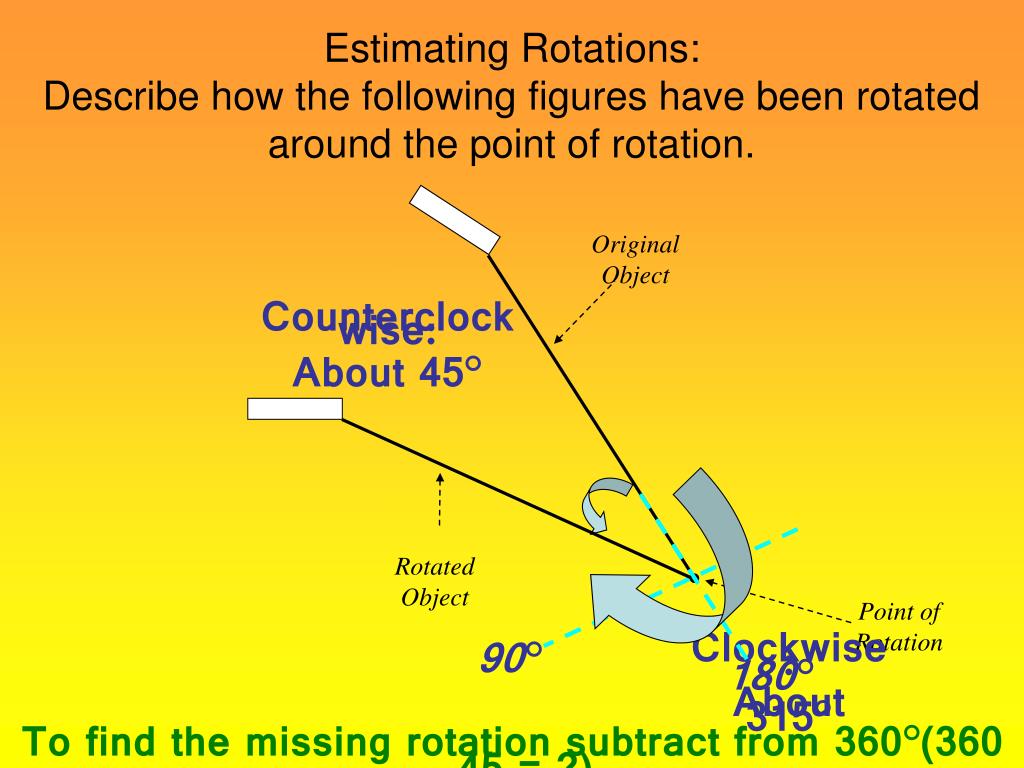
How do you find the point of rotation?
- Draw a ray from the center of rotation to the point you wish to rotate.
- Draw an angle with the center of rotation as the vertex.
- Use a compass to draw a circle (arc) with the center at the center of rotation and a radius from the center of rotation to the point you are rotating.
- Now rotate all the other points and connect the dots.
How do you find the center of rotation?
Steps to Finding the Center of Rotation
- Ask yourself how the object or shape is rotating? Is it spinning left to right, right to left, top to bottom, or in another way? ...
- Determine the point around which the object is rotating. In this case, it would be the players' index fingers.
- The point around which the object is making full rotations is the center of rotation.
How to find the center of rotation?
Method 1
- Draw a line between the corresponding points
- Construct the perpendicular bisect of these points
- Do this for each point until they cross
- That is your centre of rotation
How to change the direction of rotation?
Normally Open (N.O.) motor thermostats may be used in conjunction with controls installed by an OEM.
- Keep hands and clothing away from rotating parts.
- Determine proper rotation BEFORE coupling motor to load.
- Check rotation by jogging or bumping. Apply power to the motor leads for a short period of time, enough to just get motor shaft to rotate a slight amount ...
- Three phase - interchange any two (2) of the three (3) line leads.
What is the definition of rotation?
Rotation of an object in two dimensions around a point O. Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. A rotation is different from other types of motions: translations, ...
What is the axis of rotation?
For a particular rotation: The axis of rotation is a line of its fixed points. They exist only in n > 2. The plane of rotation is a plane that is invariant under the rotation. Unlike the axis, its points are not fixed themselves. The axis (where present) and the plane of a rotation are orthogonal.
What is rotation group?
The rotation group is a Lie group of rotations about a fixed point. This (common) fixed point is called the center of rotation and is usually identified with the origin. The rotation group is a point stabilizer in a broader group of (orientation-preserving) motions . For a particular rotation:
Why is the distinction between points and vectors erased?
When one considers motions of the Euclidean space that preserve the origin, the distinction between points and vectors, important in pure mathematics, can be erased because there is a canonical one-to-one correspondence between points and position vectors. The same is true for geometries other than Euclidean, but whose space is an affine space with a supplementary structure; see an example below. Alternatively, the vector description of rotations can be understood as a parametrization of geometric rotations up to their composition with translations. In other words, one vector rotation presents many equivalent rotations about all points in the space.
How many degrees of freedom does rotation have?
If these are ω1 and ω2 then all points not in the planes rotate through an angle between ω1 and ω2. Rotations in four dimensions about a fixed point have six degrees of freedom.
How to do a rotation in two dimensions?
In two dimensions, to carry out a rotation using a matrix, the point (x, y) to be rotated counterclockwise is written as a column vector, then multiplied by a rotation matrix calculated from the angle θ :
What are the two types of rotation?
These two types of rotation are called active and passive transformations .
What is a rotation in geometry?
Rotation. In geometry, a rotation is a type of transformation where a shape or geometric figure is turned around a fixed point. It may also be referred to as a turn.
What happens when a geometric figure rotates around a point?
Rotations in coordinate geometry. In a coordinate plane, when geometric figures rotate around a point, the coordinates of the points change. While a geometric figure can be rotated around any point at any angle, we will only discuss rotating a geometric figure around the origin at common angles.
What is the term for a parallelogram that rotates around a red dot?
On the right, a parallelogram rotates around the red dot. The term "preimage" is used to describe a geometric figure before it has been transformed and the term "image" is used to describe it after it has been transformed. For 2D figures, a rotation turns each point on a preimage around a fixed point, called the center of rotation, ...
What happens when you rotate 90 degrees clockwise?
A rotation of 90° counterclockwise around the origin changes the position of a point (x, y) such that it becomes (-y, x). A rotation of 90° clockwise changes the point such that (x, y) becomes (y, -x).
What is the symmetry of a shape?
Rotational symmetry. A geometric figure or shape has rotational symmetry about a fixed point if it can be rotated back onto itself by an angle of rotation of 180° or less. Below are several geometric figures that have rotational symmetry.
What is the center of rotation?
Rotations are Direct Isometries. " Center " is the 'center of rotation.'. This is the point around which you are performing your mathematical rotation. " Degrees " stands for how many degrees you should rotate. A positive number usually by convention means counter clockwise.
What does a positive number mean in geometry?
A positive number usually by convention means counter clockwise. A rotation is a direct isometry , which means that both the distance and orientation are preserved. As you can see in diagram 1 below, triangle △ A B C is rotated by 90 ∘ to its image △ A ′ B ′ C ′ . And the distance between each of the vertices of the preimage is maintained in its ...
What is a rotation in math?
Concept Development. (R1) A rotation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle. (R2) A rotation preserves lengths of segments. (R3) A rotation preserves degrees of angles.
What do students know about rotations?
Students know that rotations preserve lengths of segments and degrees of measures angles. Students know that rotations move parallel lines to parallel lines.
Which direction does a positive degree of rotation move the figure in?
Positive degrees of rotation move the figure in a counterclockwise direction. Negative degrees of rotation move the figure in a clockwise direction. (R1) A rotation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle. (R2) A rotation preserves lengths of segments.

Overview
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from ot…
Related definitions and terminology
The rotation group is a Lie group of rotations about a fixed point. This (common) fixed point is called the center of rotation and is usually identified with the origin. The rotation group is a point stabilizer in a broader group of (orientation-preserving) motions.
For a particular rotation:
• The axis of rotation is a line of its fixed points. They exist only in n > 2.
Definitions and representations
A motion of a Euclidean space is the same as its isometry: it leaves the distance between any two points unchanged after the transformation. But a (proper) rotation also has to preserve the orientation structure. The "improper rotation" term refers to isometries that reverse (flip) the orientation. In the language of group theory the distinction is expressed as direct vs indirect isometries in the Euclidean …
Importance
Rotations define important classes of symmetry: rotational symmetry is an invariance with respect to a particular rotation. The circular symmetry is an invariance with respect to all rotation about the fixed axis.
As was stated above, Euclidean rotations are applied to rigid body dynamics. Moreover, most of mathematical formalism in physics (such as the vector calculus) is rotation-invariant; see rotation for …
Generalizations
The complex-valued matrices analogous to real orthogonal matrices are the unitary matrices , which represent rotations in complex space. The set of all unitary matrices in a given dimension n forms a unitary group of degree n; and its subgroup representing proper rotations (those that preserve the orientation of space) is the special unitary group of degree n. These complex rotations are important in the context of spinors. The elements of are used to parametrize three-…
See also
• Aircraft principal axes
• Charts on SO(3)
• Coordinate rotations and reflections
• CORDIC algorithm
• Hyperbolic rotation
Footnotes
1. ^ Weisstein, Eric W. "Alibi Transformation." From MathWorld--A Wolfram Web Resource.
2. ^ Weisstein, Eric W. "Alias Transformation." From MathWorld--A Wolfram Web Resource.
3. ^ Lounesto 2001, p. 30.