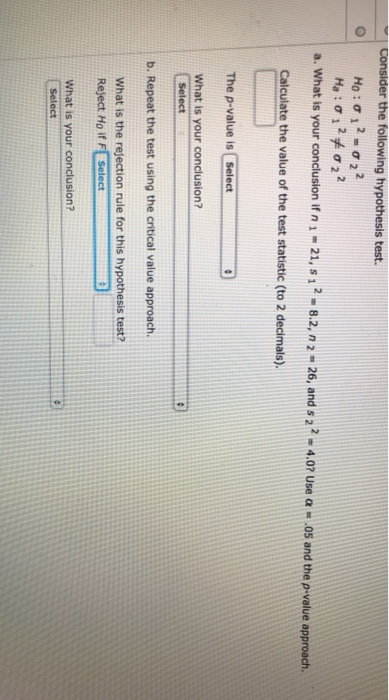
There are usually two methods by which the rejection rule can be implemented. Under critical value, the comparison between the test statistics and some cutoff value is made and based on that the verdict is decided whether the null hypothesis will be accepted or rejected.
How to determine the critical value of a test?
Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted α (greek letter "alpha") and is called the " significance level of the test " — is small (typically 0.01, 0.05, or 0.10).
What are the rejection regions of the decision rule?
The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively.
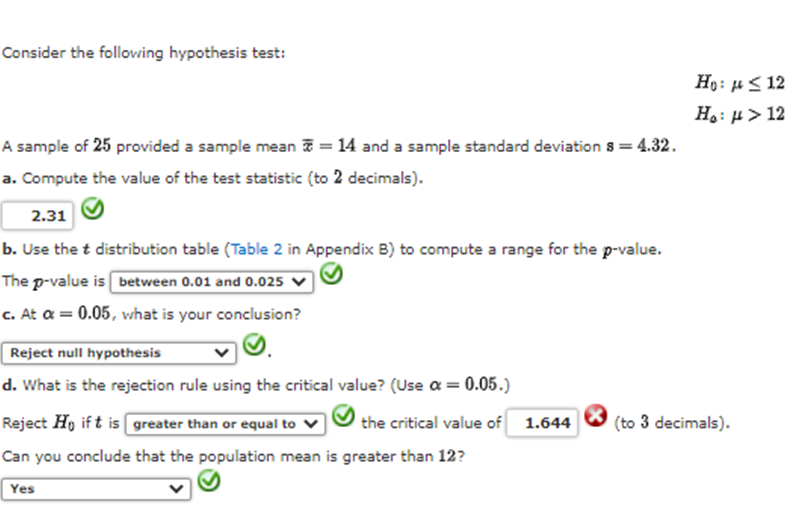
Should I reject or reject Ho?
Reject Ho. There is sufficient evidence to conclude that u > 12. Do not reject Ho. There is insufficient evidence to conclude that u > 12.
How can I increase the precision of the critical value calculator?
Go to the advanced mode of the critical value calculator if you need to increase the precision with which the critical values are computed. Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N (0,1).

How do you find the critical value and rejection region?
One or two of the sections is the “rejection region“; if your test value falls into that region, then you reject the null hypothesis. A one tailed test with the rejection in one tail. The critical value is the red line to the left of that region.
What is the critical value for rejecting the null hypothesis?
Critical values for a test of hypothesis depend upon a test statistic, which is specific to the type of test, and the significance level, \alpha, which defines the sensitivity of the test. A value of \alpha = 0.05 implies that the null hypothesis is rejected 5 % of the time when it is in fact true.
What is the relationship between critical value and rejection area?
A critical value is a point on the distribution of the test statistic under the null hypothesis that defines a set of values that call for rejecting the null hypothesis. This set is called critical or rejection region. Usually, one-sided tests have one critical value and two-sided test have two critical values.
What is the critical value rule?
The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true.
How do you reject the null hypothesis?
Rejecting or failing to reject the null hypothesis If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis.
What is the critical value at the 0.05 level of significance?
The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value. For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.
How do you determine the rejection region?
Rejection Regions and Alpha Levels You, as a researcher, choose the alpha level you are willing to accept. For example, if you wanted to be 95% confident that your results are significant, you would choose a 5% alpha level (100% – 95%). That 5% level is the rejection region.
What is the rejection region in statistics?
A critical region, also known as the rejection region, is a set of values for the test statistic for which the null hypothesis is rejected. i.e. if the observed test statistic is in the critical region then we reject the null hypothesis and accept the alternative hypothesis.
What is the relationship between the rejection region and the value of test statistic in making conclusion?
The rejection region is the region where, if our test statistic falls, then we have enough evidence to reject the null hypothesis. If we consider the right-tailed test, for example, the rejection region is any value greater than c 1 − α , where c 1 − α is the critical value.
What does rejecting the null hypothesis mean?
Rejecting the Null Hypothesis Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
What does fail to reject the null hypothesis mean?
When we fail to reject the null hypothesis when the null hypothesis is false. The “reality”, or truth, about the null hypothesis is unknown and therefore we do not know if we have made the correct decision or if we committed an error. We can, however, define the likelihood of these events.
What is the critical value formula?
In statistics, critical value is the measurement statisticians use to calculate the margin of error within a set of data and is expressed as: Critical probability (p*) = 1 - (Alpha / 2), where Alpha is equal to 1 - (the confidence level / 100).
What happens if the test statistic is more extreme than the critical value?
If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.
When to reject null hypothesis?
If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.
What is the critical value of H0?
There are two critical values for the two-tailed test H0 : μ = 3 versus HA : μ ≠ 3 — one for the left-tail denoted -t( α /2, n - 1) and one for the right-tail denoted t( α /2, n - 1). The value -t( α /2, n - 1) is the t -value such that the probability to the left of it is α /2, and the value t( α /2, n - 1) is the t -value such that the probability to the right of it is α /2. It can be shown using either statistical software or a t -table that the critical value -t0.025,14 is -2.1448 and the critical value t0.025,14 is 2.1448. That is, we would reject the null hypothesis H0 : μ = 3 in favor of the alternative hypothesis HA : μ ≠ 3 if the test statistic t * is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.
What is a critical value?
In hypothesis testing, critical values are one of the two approaches which allow you to decide whether to retain or reject the null hypothesis. The other approach is to calculate the p-value.
Critical value definition
To determine critical values, you need to know the distribution of your test statistic under the assumption that the null hypothesis holds. Critical values are then the points on the distribution which have the same probability as your test statistic, equal to the significance level α.
How to calculate critical values?
The formulae for the critical values involve the quantile function, Q, which is the inverse of the cumulative distribution function ( cdf) for the test statistic distribution (calculated under the assumption that H₀ holds!): Q = cdf -1
How to use this critical value calculator?
Now that you have found our critical value calculator, you no longer need to worry how to find critical value for all those complicated distributions! Here are the steps you need to follow:
Z critical values
Use the Z (standard normal) option if your test statistic follows (at least approximately) the standard normal distribution N (0,1).
t critical values
Use the t-Student option if your test statistic follows the t-Student distribution. This distribution is similar to N (0,1), but its tails are fatter - the exact shape depends on the number of degrees of freedom.
F critical values
Finally, choose F (Fisher-Snedecor) if your test statistic follows the F-distribution. This distribution has a pair of degrees of freedom.
What are the two types of errors in a hypothesis test?
In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).
What does a p-value represent?
Many investigators inappropriately believe that the p-value represents the probability that the null hypothesis is true. P-values are computed based on the assumption that the null hypothesis is true.