what makes a polynomial

Polynomials are composed of some or all of the following:

• Variables - these are letters like x, y, and b
• Constants - these are numbers like 3, 5, 11. ...
• Exponents - exponents are usually attached to variables but can also be found with a constant. ...
• Addition, subtraction, multiplication, and division - For example, you can have 2x (multiplication), 2x+5 (multiplication and addition), and x-7 (subtraction.)

Full Answer

How do you create a polynomial?

A Polynomial can be expressed in terms that only have positive integer exponents and the operations of addition, subtraction, and multiplication. In other words, it must be possible to write the expression without division. It's easiest to understand what makes something a polynomial equation by looking at examples and non examples as shown below.

What are the monomials which make up a polynomial called?

The monomials that make up a polynomial are called polynomial terms. If a polynomial consists of two terms, then such a polynomial is called a binomial. For example, the polynomial x + y is a binomial. If a polynomial has three terms, then such a polynomial is called a trinomial. For example, a polynomial x + y + z is a trinomial.

How to determine a polynomial?

• If the graph crosses the x -axis and appears to be linear near the intercept, the root is unique.
• If the graph touches the x -axis and bounces, the root has an even multiplicity.
• If the graph crosses the x -axis at a root, then the root has odd multiplicity.
• The sum of the multiplicities is the degree n of the polynomial.

What makes an equation not a polynomial?

Polynomials are composed of some or all of the following:

• Variables - these are letters like x, y, and b
• Constants - these are numbers like 3, 5, 11. ...
• Exponents - exponents are usually attached to variables but can also be found with a constant. ...
• Addition, subtraction, multiplication, and division - For example, you can have 2x (multiplication), 2x+5 (multiplication and addition), and x-7 (subtraction.)

How do you know if it's a polynomial?

All the exponents in the algebraic expression must be non-negative integers in order for the algebraic expression to be a polynomial. As a general rule of thumb if an algebraic expression has a radical in it then it isn't a polynomial.

What defines a polynomial?

Definition of polynomial (Entry 1 of 2) : a mathematical expression of one or more algebraic terms each of which consists of a constant multiplied by one or more variables raised to a nonnegative integral power (such as a + bx + cx2) polynomial.

What makes things not a polynomial?

Rules: What ISN'T a Polynomial Polynomials cannot contain division by a variable. For example, 2y2+7x/4 is a polynomial because 4 is not a variable. However, 2y2+7x/(1+x) is not a polynomial as it contains division by a variable. Polynomials cannot contain negative exponents.

What makes something a polynomial equation?

An equation formed with variables, exponents, and coefficients together with operations and an equal sign is called a polynomial equation. It has different exponents. The higher one gives the degree of the equation.

What is polynomial and non polynomial?

Identifying Polynomials The polynomials can be identified by noting which expressions contain only the operations of addition, subtraction, multiplication, and non-negative integer exponents. The non-polynomial expressions will be the expressions which contain other operations.

Is 12x a polynomial?

12x is a polynomial.

Which number Cannot be a polynomial?

A polynomial cannot have any of the following: A variable with a negative exponent. Division by a variable (this can lead to negative exponents). A variable with a fractional exponent (unless the fraction reduces to a whole number).

What is non polynomial?

(complexity) The set or property of problems for which no polynomial-time algorithm is known. This includes problems for which the only known algorithms require a number of steps which increases exponentially with the size of the problem, and those for which no algorithm at all is known.

What are the rules of polynomials?

Rules for an Expression to be a Polynomial An algebraic expression should not consist of – Square root of variables. Fractional powers on the variables. Negative powers on the variables. Variables in the denominators of any fractions.

What is a polynomial in math?

In mathematics, a polynomial is an expression consisting of variables (also called indeterminates) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. An example of a polynomial of a single indeterminate, x, is x2 − 4x + 7.

What is a zero polynomial?

whose coefficients are all equal to 0. The corresponding polynomial function is the constant function with value 0, also called the zero map. The zero polynomial is the additive identity of the additive group of polynomials.

What are polynomials made of?

A polynomial is an algebraic expression made up of two or more terms. Polynomials are composed of some or all of the following: 1 Variables - these are letters like x, y, and b 2 Constants - these are numbers like 3, 5, 11. They are sometimes attached to variables but are also found on their own. 3 Exponents - exponents are usually attached to variables but can also be found with a constant. Examples of exponents include the 2 in 5² or the 3 in x³. 4 Addition, subtraction, multiplication, and division - For example, you can have 2x (multiplication), 2x+5 (multiplication and addition), and x-7 (subtraction.)

What happens when you multiply polynomials?

Polynomials often represent a function. And if you graph a polynomial of a single variable, you'll get a nice, smooth, curvy line with continuity (no holes.)

What polynomials cannot contain division?

There are a few rules as to what polynomials cannot contain: Polynomials cannot contain division by a variable. For example, 2y2+7x/4 is a polynomial because 4 is not a variable. However, 2y2+7x/ (1+x) is not a polynomial as it contains division by a variable. Polynomials cannot contain negative exponents. You cannot have 2y-2+7x-4.

What is a polynomial with a degree of two called?

If a polynomial has a degree of two, it is often called a quadratic . If it has a degree of three, it can be called a cubic. Polynomials with degrees higher than three aren't usually named (or the names are seldom used.) You can do numerous operations on polynomials.

How many exponents are there in 5y2x?

The second term (5y2x) has two exponents. They are 2 (from 5y2) and 1 (from x, this is because x is the same as x1.) The exponents in this term add up to three. The last term (4x2) only has one exponent, 2, so its degree is just two. Since the first term has the highest degree (the 4th degree), it is the leading term.

What are the rules for polynomials?

What are the rules for polynomials? The short answer is that polynomials cannot contain the following: division by a variable, negative exponents, fractional exponents, or radicals.

What are some examples of exponents?

Exponents - exponents are usually attached to variables but can also be found with a constant. Examples of exponents include the 2 in 5² or the 3 in x³.

What is a Polynomial?

A polynomial is defined as an expression which is composed of variables, constants and exponents, that are combined using the mathematical operations such as addition , subtraction, multiplication and division (No division operation by a variable). Based on the numbers of terms present in the expression, it is classified as monomial, binomial, and trinomial. Examples of constants, variables and exponents are as follows:

What is the degree of a polynomial?

The degree of a polynomial is defined as the highest degree of a monomial within a polynomial. Thus, a polynomial equation having one variable which has the largest exponent is called a degree of the polynomial.

How to tell if polynomial is divisible by binomial?

Polynomial P (x) is divisible by binomial (x – a) if and only if P (a) = 0.

What is the difference between subtracting and adding polynomials?

Subtracting polynomials is similar to addition, the only difference being the type of operation. So, subtract the like terms to obtain the solution. It should be noted that subtraction of polynomials also results in a polynomial of the same degree.

What happens if a polynomial is divisible by a polynomial Q?

If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.

What is a monomial expression?

A monomial is an expression which contains only one term. For an expression to be a monomial, the single term should be a non-zero term. A few examples of monomials are:

What is the result of a polynomial divided by Q?

A polynomial P (x) divided by Q (x) results in R (x) with zero remainders if and only if Q (x) is a factor of P (x).

What is a Polynomial?

What is an expression? An expression is a mathematical statement without an equal-to sign (=). Coming back to polynomials, the definition of the polynomial can be given as: "A polynomial is a type of expression in which the exponents of all variables should be a whole number ". Let us understand this by taking an example: 3x 2 + 5. In the above polynomial, there are certain terms that we need to understand. Here, x is known as the variable. 3 which is multiplied to x 2 has a special name. We denote it by the term "coefficient". 5 is known as the constant. The power of the variable x is two.

What is like terms in polynomials?

Like terms in polynomials are those terms which have the same variable and same power. Terms that have different variables and different powers are known as unlike terms. Hence, if a polynomial has two variables, then all the same powers of any ONE variable will be known as like terms.

How to add and subtract polynomials?

Addition and Subtraction of Polynomials 1 Terms in a polynomial can be only separated by the '+' or '-' sign. 2 For any expression to become a polynomial, the power of the variable should be a whole number. 3 The addition and subtraction of a polynomial are possible between like terms only. 4 All the numbers in the universe are called constant polynomials.

What is the theorem 4?

Theorem 4: If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.

What is the difference between a binomial and a trinomial?

Binomial is a type of polynomial that has two terms. For example x+5, y 2 +5, and 3x 3 −7. While a Trinomial is a type of polynomial that has three terms. For example 3x 3 +8x−5, x+y+z, and 3x+y−5. However, based on the degree of the polynomial, polynomials can be classified into 4 major types:

What is a polynomial expression?

A polynomial expression has terms connected by the addition or subtraction operators. There are different properties and theorems on polynomials based on the type of polynomial and the operation performed. Some of these are as given below,

What is factorization of polynomials?

Factorization of polynomials is the process by which we decompose a polynomial expression into the form of the product of its irreducible factors, such that the coefficients of the factors are in the same domain as that of the main polynomial. There are different techniques that can be followed for factoring polynomials, given as,

What is a polynomial in math?

In mathematics, a polynomial is an expression consisting of variables (also called indeterminates) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7.

Where does the word "polynomial" come from?

It was derived from the term binomial by replacing the Latin root bi- with the Greek poly- . The word polynomial was first used in the 17th century.

What is the name of the polynomial with no terms?

The names for the degrees may be applied to the polynomial or to its terms. For example, the term 2x in x2 + 2x + 1 is a linear term in a quadratic polynomial. The polynomial 0, which may be considered to have no terms at all, is called the zero polynomial. Unlike other constant polynomials, its degree is not zero.

What is a one term polynomial called?

Polynomials can be classified by the number of terms with nonzero coefficients, so that a one-term polynomial is called a monomial, a two-term polynomial is called a binomial, and a three-term polynomial is called a trinomial. The term "quadrinomial" is occasionally used for a four-term polynomial.

How to tell if a polynomial is a divisor?

If R is an integral domain and f and g are polynomials in R[x], it is said that f divides g or f is a divisor of g if there exists a polynomial q in R[x] such that f q = g . One can show that every zero gives rise to a linear divisor, or more formally, if f is a polynomial in R[x] and r is an element of R such that f(r) = 0, then the polynomial ( x − r) divides f. The converse is also true. The quotient can be computed using the polynomial long division.

What is a constant term with no indeterminates?

A term with no indeterminates and a polynomial with no indeterminates are called, respectively, a constant term and a constant polynomial. The degree of a constant term and of a nonzero constant polynomial is 0. The degree of the zero polynomial 0 (which has no terms at all) is generally treated as not defined (but see below).

When does a non-constant polynomial function tend to infinity?

A non-constant polynomial function tends to infinity when the variable increases indefinitely (in absolute value ). If the degree is higher than one, the graph does not have any asymptote. It has two parabolic branches with vertical direction (one branch for positive x and one for negative x ).

Why is the first one not a polynomial?

The first one isn’t a polynomial because it has a negative exponent and all exponents in a polynomial must be positive. To see why the second one isn’t a polynomial let’s rewrite it a little. 5√x −x +x2 =5x1 2 −x+x2 5 x − x + x 2 = 5 x 1 2 − x + x 2.

How many variables can a polynomial be?

We can also talk about polynomials in three variables, or four variables or as many variables as we need. The vast majority of the polynomials that we’ll see in this course are polynomials in one variable and so most of the examples in the remainder of this section will be polynomials in one variable.

What is the degree of a polynomial in one variable?

The degree of a polynomial in one variable is the largest exponent in the polynomial.

What is a monomial and binomial?

A monomial is a polynomial that consists of exactly one term. A binomial is a polynomial that consists of exactly two terms. Finally, a trinomial is a polynomial that consists of exactly three terms. We will use these terms off and on so you should probably be at least somewhat familiar with them.

When we have a coefficient, do we do the exponentiation first?

When we’ve got a coefficient we MUST do the exponentiation first and then multiply the coefficient.

Do you need parentheses around the second term?

This time the parentheses around the second term are absolutely required. We are subtracting the whole polynomial and the parenthesis must be there to make sure we are in fact subtracting the whole polynomial.

Do you need parenthesis when adding two polynomials?

In this case the parenthesis are not required since we are adding the two polynomials. They are there simply to make clear the operation that we are performing. To add two polynomials all that we do is combine like terms. This means that for each term with the same exponent we will add or subtract the coefficient of that term.

What is the expression for a polynomial?

It can be expressed in terms of a polynomial. The polynomial equation is used to represent the polynomial function. Generally, a polynomial is denoted as P (x). The greatest exponent of the variable P (x) is known as the degree of a polynomial.

Why are polynomials useful?

Polynomial functions are useful to model various phenomena. In Physics and Chemistry, unique groups of names such as Legendre, Laguerre and Hermite polynomials are the solutions of important issues.

What is a polynomial equation?

Polynomial equations are the equations formed with variables exponents and coefficients. The equation can have various distinct components , where the higher one is known as the degree of exponents. Polynomial Equations can be solved with respect to the degree and variables exist in the equation.

What is a polynomial function with a degree of 1?

Linear Polynomial Function - Polynomial functions with a degree of 1 are known as Linear Polynomial functions. Quadratic Polynomial Function - Polynomial functions with a degree of 2 are known as Quadratic Polynomial functions.

What is the most common mathematical equation?

Polynomial functions are the most easiest and commonly used mathematical equation. It can be expressed in terms of a polynomial. The polynomial equation is used to represent the polynomial function. Generally, a polynomial is denoted as P (x). The greatest exponent of the variable P (x) is known as the degree of a polynomial. It is important to understand the degree of a polynomial as it describes the behavior of function P (x) when the value of x gets enlarged. The domain of polynomial functions is entirely real numbers (R).

What are some examples of polynomial functions?

Some of the examples of polynomial functions are given below: 2x² + 3x +1 = 0. 4x -5 = 3.

What is a parabola graph?

Graph: A parabola is a curve with a single endpoint known as the vertex. A parabola is a mirror-symmetric curve where each point is placed at an equal distance from a fixed point called the focus.

What cannot be a polynomial?

So, what cannot be a polynomial? An expression with a variable with negative or fractional exponents, division by a variable, or a variable inside a radical is not a polynomial. However, a polynomial may contain coefficients that are negative, fractions, or even radicals, as long as the polynomial is defined over the real numbers.

How many terms can a polynomial have?

A polynomial can have one term. This one term could have any power of x, as long as the exponent is a nonnegative integer.

Can A Polynomial Have A Variable In The Denominator?

A polynomial cannot have a variable in the denominator of any term. In other words, we are only adding, subtracting, and multiplying powers of x – we are not dividing them.

Can A Polynomial Have A Square Root?

A polynomial cannot have a square root. The reason is that this would involve a power that is not a whole number (since a square root is a power of 1/2).

Can A Polynomial Be A Fraction?

A polynomial can be a fraction in certain cases, and it can contain one or more terms that are fractions. We just need to avoid variables in the denominators of these fractions.

Can A Polynomial Have Two Variables?

A polynomial can have two variables. In fact, a polynomial can have three variables or more – as many as you like.

Can A Polynomial Have No Constant Term?

A polynomial can have no constant term. Another way to say this is that the constant term is zero.

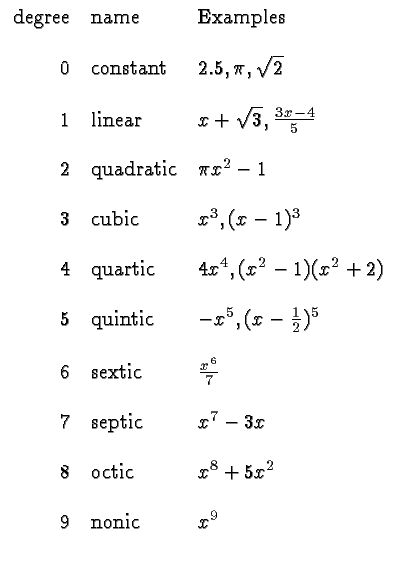
What Is A polynomial?

See more on byjus.com

Degree of A Polynomial

Terms of A Polynomial

Types of Polynomials

Properties

Polynomial Equations

Polynomial Functions

Solving Polynomials

Polynomial Operations

Polynomial Examples