what number is real but not rational

What is an integer that is not a real number?

Square root of -1 is also not a real number, and therefore it is referred to as an imaginary number. Integers are types of whole numbers that are not in the form of fractions. Integers can be both positive and negative. Integers are actually subset of real numbers.

How to determine if a number is rational or not?

• If its simply a number with no decimals, I may be looking at natural or integer numbers. ...
• If I am given a small decimal number, then yes it is rational. ...
• If its a number inside a root, something like x n m then I can say its irrational provided that n ≠ m k where k ∈ Z
• Irrational numbers are non repeating, non terminating numbers. ...

Is real number is always a rational number?

Rational and Irrational numbers both are real numbers but different with respect to their properties. A rational number is the one which can be represented in the form of P/Q where P and Q are integers and Q ≠ 0. But an irrational number cannot be written in the form of simple fractions.

Is 11 a real number?

Therefore, √ 11 is an irrational number. 17 34: Because it is a fraction, 17 34 is a rational number. Simplify and divide. So, 17 34 is rational and a terminating decimal. 0.3033033303333… is not a terminating decimal.

What is a real number that is not irrational?

Real numbers are numbers that include both rational and irrational numbers. Rational numbers such as integers (-2, 0, 1), fractions(1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.

What is an example of a real number that is not rational?

π is an irrational number that has a value of 3.142…and is a never-ending and non-repeating number. √2 is an irrational number, as it cannot be simplified.

Is a real number an irrational number?

Irrational Numbers Definition: Irrational numbers are real numbers that cannot be represented as a simple fraction. These cannot be expressed in the form of ratio, such as p/q, where p and q are integers, q≠0. It is a contradiction of rational numbers.

Is 0.0 is a rational number?

Answer: Yes, 0 is a rational number because it has a non-zero denominator. Since the number 0 can also be written as 0/1.

Is 3.14 a rational number?

Is 3.14 a rational number? Yes, 3.14 is a rational number because it is terminating.

Is 5.34 a rational number?

Furthermore, the numerator and the denominator of the fraction above are integers. Therefore, we can conclude that the answer to "Is 5.34 a rational number?" is yes.

What are 5 examples of irrational numbers?

For example, √5 is an irrational number. We can prove that the square root of any prime number is irrational. So √2, √3, √5, √7, √11, √13, √17, √19 … are all irrational numbers.

Are all real numbers rational?

If we combine the rational numbers and the irrational numbers, we get real numbers. Hence, all real numbers are not rational numbers because real numbers also contain irrational numbers. Hence, the given statement is false.

Why is 7 not a rational number?

The number 7 is a rational number. Rational numbers are defined as numbers that result when two integers are divided. To obtain the rational number 7, you can divide the integer 7 by the integer 1. Because you can obtain the number 7 by dividing two integers, 7 is called a rational number.

Why every real number is not rational?

If we combine the rational numbers and the irrational numbers, we get real numbers. Hence, all real numbers are not rational numbers because real numbers also contain irrational numbers.

Is 1.333333 A rational?

Here's a hint: if you're working with a number with a long line of different decimals, then your number is irrational! If you're working with an integer or a number with terminal or repeating decimals (like 1.333333), then your number is rational!

What are 5 examples of rational numbers?

Examples of rational numbers are: -2 = -2/1, -5 = -5/1, -14 = -14/1, 1/2, 2/3, 5/8, 3/4, 17/5, . 6 = 6/10 = 3/5, . 25 = 1/4, . 33 = 33/100, 2¾ = 11/4, 3⅓ = 10/3, .

What is the next level of numbers?

The next level of number is built out of integers. These are called rational numbers. We form them by taking integers and making every possible fraction out of them—i.e., a/b, where a is an integer and b is an integer (but b is not equal to zero). This is the familiar fraction we know from school. The number a is called the numerator and b the denominator.

How to find square root of a number?

Finding the square root of a number means finding two numbers that are equal and, when you multiply them together, create the original number. For example, √4 is 2 because 2×2 = 4, i.e., two equal numbers that multiply together to make 4 are 2. But √2 has no fraction answer. The proof for this requires some algebra.

Why are fractions so stressful?

You’re probably familiar with fractions: Fractions are often a source of stress in math because of how difficult the rules can be for adding and multiplying them.

What is the symbol for real numbers?

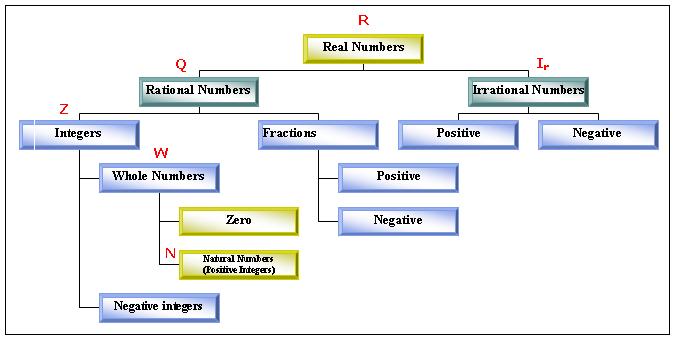
We call the complete collection of numbers (i.e., every rational, as well as irrational, number) real numbers. They have the symbol R.

What is the name of the number that goes all the way to the left?

Recall that integers, Z, are all the negative numbers that go all the way to the left (to “negative infinity”) joined to all the natural numbers, N, that extend forever to the right (positive infinity):

Can rational numbers be fractions?

There are many numbers we can make with rational numbers. We can make any fraction. But are these all the possible numbers? The answer is no, but let me show you why, by way of an example.

Is there a rational square root for primes?

The proof for this requires some algebra. In fact, if you recall our prime numbers from yesterday, then it can also be proven that there are no rational square roots for any prime. It also has been proven that there are infinitely many primes.

How to Classify Rational and Irrational Numbers?

Let us see how to identify rational and irrational numbers based on the given set of examples.

What are some examples of irrational numbers?

Examples of Irrational Numbers 1 5/0 is an irrational number, with the denominator as zero. 2 π is an irrational number which has value 3.142…and is a never-ending and non-repeating number. 3 √2 is an irrational number, as it cannot be simplified. 4 0.212112111…is a rational number as it is non-recurring and non-terminating.

What is rational number?

Rational numbers are numbers which can be expressed as a fraction and also as positive numbers, negative numbers and zero. It can be written as p/q, where q is not equal to zero. The word rational is derived from the word ‘ratio’, which actually means a comparison of two or more values or integer numbers and is known as a fraction.

What is the difference between rational and irrational numbers?

Rational numbers are the numbers that can be expressed in the form of a ratio (P/Q & Q≠0) and irrational numbers cannot be expressed as a fraction. But both the numbers are real numbers and can be represented in a number line.

What are some rules based on arithmetic operations such as addition and multiplication performed on the rational number?

Here are some rules based on arithmetic operations such as addition and multiplication performed on the rational number and irrational number. #Rule 1: The sum of two rational numbers is also rational. #Rule 2: The product of two rational number is rational.

Can irrational numbers be written as fractions?

Now, let us elaborate, irrational numbers could be written in decimals but not in the form of fractions, which means it cannot be written as the ratio of two integers. Irrational numbers have endless non-repeating digits after the decimal point. Below is an example of the irrational number: Example: √8 =2.828….

Is the ellipsis after 3.605551275 irrational?

The ellipsis (…) after 3.605551275 shows that the number is non-terminating and also there is no repeated pattern here. Therefore, it is ir rational.

How to do a repeating decimal expansion?

Conversely, suppose we have a rational number . Perform the division of by using the long division algorithm. Every step of the division will have one of remainders. If the remainder eventually becomes zero, then the algorithm stops and the rational number’s decimal expansion terminates. If the remainder never becomes zero, then the same remainder will eventually reappear after at most steps, in which case the same string of decimal digits (at most digits long) will appear over and over. Thus will have a repeating decimal expansion, as required.

What is an integer?

An integer is defined as: a whole number; a number that is not a fraction.

What are the two types of numbers?

Numbers are of two kinds: Imaginary and Real.

What is the trite answer to squared?

The trite response is of course that the answer is √2 [8]. But this is just shorthand for “number which when squared equals 2” so we have perhaps not advanced our cause so very far.

What is a real number?

A real number is any number on the number line.

Is a real number rational?

Since is equivalent, logically, to , we instead prove that a real number is rational if and only if it has a repeating or terminating decimal expansion.

Is real no. rational or irrational?

Since real no. Can be further categorised into rational no. And irrational no .

What are irrational numbers?

Numbers like √2, √x (where x is a positive rational number but not the square of a rational number), π etc. cannot be expressed as ratio of two integers like rational numbers, but can be represented on real number line. These numbers are called irrational numbers.

Is a rational number real?

Although all rational numbers are real numbers, there are some numbers (irrational numbers) which are not rational numbers.

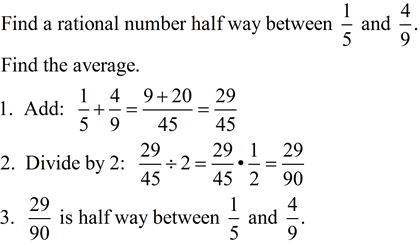
Definitions

See more on byjus.com

How to Classify Rational and Irrational numbers?

Properties of Rational and Irrational Numbers

Solved Problems