
A quadratic sequence is an ordered set with constant second differences (the first differences increase by the same value each time). For example, the set {0, 1, 4, 9, 16, …} is a quadratic sequence, since the differences between terms are 1, 3, 5, 7, …, which increase by 2 at each step.
How to find the nth term of a quadratic sequence?
What are the 5 steps to find the nth term of a sequence?
- If there is no remainder after subtracting an 2 from the original sequence, step 4 is not needed.
- If the same constant remains for each term after the subtraction, we just add it to an 2.
- If a sequence is generated after step 3, continue with step 4.
What is the formula to the sequence?
nᵗʰ Term of Geometric Sequence Formula
- a = first term of the geometric sequence
- r = common ratio of the geometric sequence
- aₙ = n th term
What is the nth term for this quadratic sequence?
The second method to find the nth term of a quadratic sequence should make this clear. As we said before, the nth term rule of any quadratic sequence can be written in the form an2 + bn + c. So, lets substitute the numbers 1 to 5 for n to write out the first 5 terms of the sequence an2 + bn + c.
What does solving a quadratic mean?
The terms a, b and c are also called quadratic coefficients. The solutions to the quadratic equation are the values of the unknown variable x, which satisfy the equation. These solutions are called roots or zeros of quadratic equations. The roots of any polynomial are the solutions for the given equation.
How do you find the quadratic sequence?
0:564:11nth term of a quadratic sequence - the easy way - GCSE level 6+ - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo what we're doing is we're saying the first two numbers the difference between the first twoMoreSo what we're doing is we're saying the first two numbers the difference between the first two numbers is 3 and that equals the formula.
What is the rule of a quadratic sequence?
Quadratic sequences always include an n2 term. The difference between each term in a quadratic sequence is not equal, but the second difference between each term in a quadratic sequence is equal. Quadratic sequences can also be called quadratic algebraic sequences.
What is linear and quadratic sequence?
The terms in the quadratic sequence appear in the linear sequence with an increasing number of terms between them - one number between the first two terms, then two between the second and third, three between the third and the fourth and so on.
How do you know if a sequence is linear or quadratic?
Using Differences to Determine the Model By finding the differences between dependent values, you can determine the degree of the model for data given as ordered pairs. If the first difference is the same value, the model will be linear. If the second difference is the same value, the model will be quadratic.
Is a quadratic sequence geometric?
Quadratic sequences have a constant second difference. Linear sequences have a constant first difference. Geometric sequences share common multiplying factor rather than common difference.
How do you find the first three terms of a quadratic sequence?
0:004:03Quadratic Number Sequences. How To Work Out The First 3 ... - YouTubeYouTubeStart of suggested clipEnd of suggested clipHere so it'll be one squared plus three so you do the squaring bit first so one squared is one timesMoreHere so it'll be one squared plus three so you do the squaring bit first so one squared is one times one so that is one plus 3 so 103 gives an answer of 4 so 4 is our first.
What is a quadratic sequence for kids?
Quadratic sequences Sequences are sets of numbers that are connected in some way. In a quadratic sequence, the difference between each term increases, or decreases, at a constant rate. Maths. Patterns and sequences.
What is linear sequence?
A number pattern which increases (or decreases) by the same amount each time is called a linear sequence. The amount it increases or decreases by is known as the common difference.
How do you write a quadratic equation from a pattern?
4:3017:43Quadratic Patterns Video - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo that's plus five our next one is plus seven and our next one is plus nine now again we noticeMoreSo that's plus five our next one is plus seven and our next one is plus nine now again we notice that our first differences are not constant. So it's not linear.
How do u know if an equation is quadratic?
In other words, if you have a times the square of the expression following b plus b times that same expression not squared plus c equal to 0, you have an equation that is quadratic in form.
How do you know if it's a quadratic function?
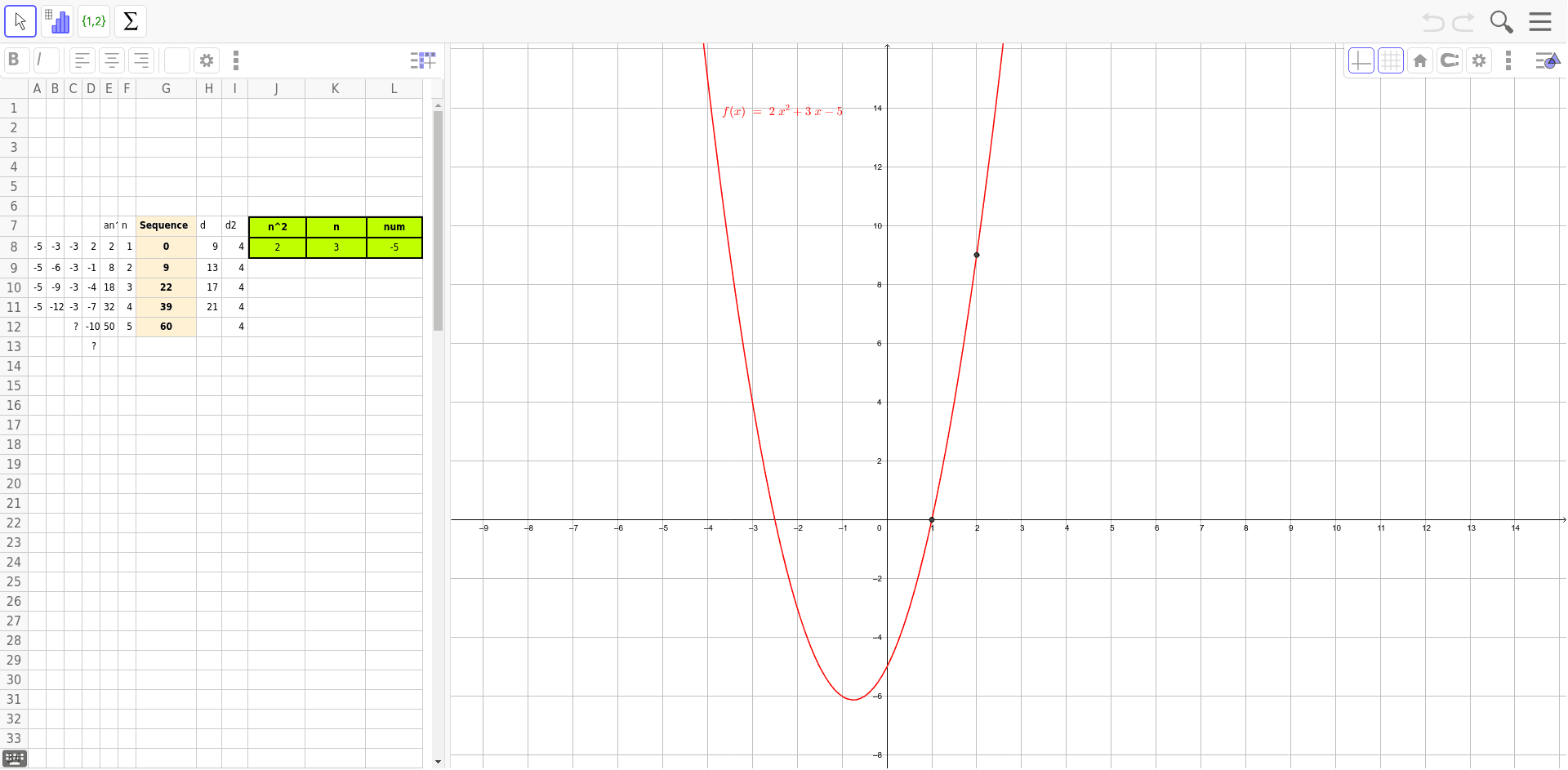
A quadratic function is one of the form f(x) = ax2 + bx + c, where a, b, and c are numbers with a not equal to zero. The graph of a quadratic function is a curve called a parabola.
How do you know if it is not a quadratic equation?
So, to check if an equation is a quadratic equation, you want to make two passes through it (both sides): Does it have an x2 term appearing somewhere? If not, then it's not a quadratic equation.
How do you find the nth term of a quadratic sequence?
Finding the nth term rule of a quadratic sequence: The nth term rule of a quadratic sequence can always be written in the form an2 + bn + c. To find this rule, we need to find a, b and c....Finally, we can substitute this into the third equation:a + b + c = 6.2 + 3 + c = 6.c = 1.
How do you write a quadratic equation?
The general form of the quadratic function is: F(x) = ax^2 + bx + c, where a, b, and c are constants.
How do you write a quadratic equation from a pattern?
4:3017:43Quadratic Patterns Video - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo that's plus five our next one is plus seven and our next one is plus nine now again we noticeMoreSo that's plus five our next one is plus seven and our next one is plus nine now again we notice that our first differences are not constant. So it's not linear.
How do you find the missing terms in a quadratic sequence?
7:5411:03Quadratic patterns and sequences-Finding the missing termsYouTubeStart of suggested clipEnd of suggested clipSo we are adding two therefore the first one that's adding 4 6 at four that's ten that's adding. SixMoreSo we are adding two therefore the first one that's adding 4 6 at four that's ten that's adding. Six so that would be eight so 16 plus 8 that's 24. And then add in 10 there.
What Is A Quadratic Sequence?
To graph a quadratic sequence, assign the values x = 1, 2, 3, 4, … based on the index in the sequence. That is, the first term gets a value of x = 1, the second term gets a value of x = 2, and so forth.
How to identify a quadratic sequence?
Of course, we can identify a quadratic sequence with a table of first and second differences or by graphing the points (with the index as x-value and the corresponding sequence term as the y-value).
What is the general form of a quadratic sequence?
The general form of a quadratic sequence follows T (n) = an2 + bn + c.. So, given a sequence of numbers, your goal is to identify a, b, and c (the coefficients ).
How to tell if a sequence is quadratic?
How to Verify a Sequence is Quadratic. A sequence is an ordered list of numbers and each number in the sequence is called a term. Each term in a quadratic sequence is related by the same common second difference. It’s called a common second difference (or second order difference) because you have to find the difference between each term twice.
How are quadratic sequences related to squared numbers?
Quadratic sequences are related to squared numbers because each sequence includes a squared number an 2. For example, the formula n 2 + 1 gives the sequence: 2, 5, 10, 17, 26, …. That sequence was obtained by plugging in the numbers 1, 2, 3, … into the formula an 2:
Why is it called a second order difference?
It’s called a common second difference (or second order difference) because you have to find the difference between each term twice. Second order differences in quadratic sequence are always constant. So, to verify that a particular sequence is quadratic, find the common second difference and verify that those differences are constant.
Is 3, 12, 25, 42 63 a quadratic sequence?
The common second difference is a constant (4), so 3, 12, 25, 42 63, … is a quadratic sequence.
Formula for the n-th term
Quadratic sequences of numbers are characterized by the fact that the difference between terms always changes by the same amount. Consequently, the "difference between the differences between the sequence's terms is always the same".
Example
The following illustration shows all of the differences we're referring to in these equations, for the quadratic sequence: 6, 11, 18, 27, 38, 51 …
What is quadratic sequence?
Quadratic sequences. Quadratic sequences are sequences that include an (n^2) term. They can be identified by the fact that the differences in between the terms are not equal, but the second differences between terms are equal.
What is a sequence based on?
Sequences can be linear, quadratic or practical and based on real-life situations. Finding general rules for sequences helps find terms in sequences that would otherwise take a long time to work out.
