
Full Answer
When do you use Pythagoras' theorem in real life?
The Pythagorean theorem can be used to build staircases, roofs, and can even be used to calculate the angle for safely placing a ladder when you need to work in high areas. It’s one of the most popular mathematical rules out there because it comes in handy any time you need to create a 90 degree angle. When do you use the Pythagorean theorem?
What does the Pythagorean theorem allow us to do?
The Pythagorean theorem is useful for architects as it plays a role in determining the size and shape of structures. With the help of this theorem, they can check building proportions. An architect deals with the design of a building, and this building has to be functional, safe, and at the same time aesthetically pleasing for the environment.
What are facts about the Pythagorean theorem?
Pythagorean theorem facts for kids. In mathematics, the Pythagorean theorem or Pythagoras's theorem is a statement about the sides of a right triangle. One of the angles of a right triangle is always equal to 90 degrees. This angle is the right angle. The two sides next to the right angle are called the legs and the other side is called the ...
Is Pythagorean theorem always a right triangle?
The Pythagorean theorem can be used to solve for any unknown side of a right triangle if the lengths of the other two sides are known. The Pythagorean theorem can be used to solve for any side of an isosceles triangle as well, even though it is not a right triangle.
Where Pythagoras theorem is not applicable?
Can we apply the Pythagoras Theorem for any triangle? No, this theorem is applicable only for the right-angled triangle.
Can you use Pythagorean Theorem on all triangles?
Pythagoras' theorem only works for right-angled triangles, so you can use it to test whether a triangle has a right angle or not.
Why the Pythagorean Theorem is not enough when solving situations that involve triangles?
No, the Pythagorean theorem can only be applied to a right-angled triangle since the Pythagorean theorem expresses the relationship between the sides of the triangle where the square of the two legs is equal to the square of the third side which is the hypotenuse.
What conditions do you need before you can use the Pythagorean Theorem?
The Pythagorean Theorem is applicable only to right triangles, so, before proceeding, it's important to make sure your triangle fits the definition of a right triangle. Luckily, there is only one qualifying factor - to be a right triangle, your triangle must contain one angle of exactly 90 degrees.
Does Pythagorean Theorem work on isosceles?
The Pythagorean theorem can be used to solve for any side of an isosceles triangle as well, even though it is not a right triangle. Isosceles triangles have two sides of equal length and two equivalent angles.
Can you use sin on any triangle?
Sine Rule. The Sine Rule can be used in any triangle (not just right-angled triangles) where a side and its opposite angle are known. You will only ever need two parts of the Sine Rule formula, not all three.
Does the Pythagorean Theorem work for triangles that dont have a 90 degree angle?
If the angle is not 90 degrees, the Pythagorean Theorem doesn't help. This is where the Law of Cosines comes in. The Law of Cosines allows us to find c even when the angle between a and b is not 90 degrees.
When can you use Pythagorean Theorem in real life?
The Pythagorean Theorem is useful for two-dimensional navigation. You can use it and two lengths to find the shortest distance. … The distances north and west will be the two legs of the triangle, and the shortest line connecting them will be the diagonal. The same principles can be used for air navigation.
Does it have to be a right triangle to use Pythagorean?
Note that the Pythagorean Theorem only works with right triangles. You can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangle's other two sides, called the legs.
What is the rule for Pythagorean Theorem?
The Pythagoras theorem, also known as the Pythagorean theorem, states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle. Or, the sum of the squares of the two legs of a right triangle is equal to the square of its hypotenuse.
Does trigonometry work on all triangles?
For Trigonometric functions to work you need a hypotenuse, which you can only get in right triangles. When you are dealing with triangles other than right triangles, the solution is to draw a perpendicular line to create right triangles.
Does 12 16 and 20 make a right triangle?
There is a fourth category of triangles in which one of interior angles is of 90∘ . It is called right triangle. It can be either be Scalene or Isosceles. 1) 12,16,20 : 202=162+122 : True, hence right triangle.
How many proofs does the Pythagorean Theorem have?
This theorem may have more known proofs than any other (the law of quadratic reciprocity being another contender for that distinction); the book The Pythagorean Proposition contains 370 proofs.
Who discovered the Pythagorean theorem?
A generalization of the Pythagorean theorem extending beyond the areas of squares on the three sides to similar figures was known by Hippocrates of Chios in the 5th century BC, and was included by Euclid in his Elements:
How to prove Pythagorean proof?
We have already discussed the Pythagorean proof, which was a proof by rearrangement. The same idea is conveyed by the leftmost animation below, which consists of a large square, side a + b, containing four identical right triangles. The triangles are shown in two arrangements, the first of which leaves two squares a2 and b2 uncovered, the second of which leaves square c2 uncovered. The area encompassed by the outer square never changes, and the area of the four triangles is the same at the beginning and the end, so the black square areas must be equal, therefore a2 + b2 = c2.
What is a Pythagorean triple?
A Pythagorean triple has three positive integers a, b, and c, such that a2 + b2 = c2. In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths. Such a triple is commonly written (a, b, c).
What is the law of cosines?
A generalization of this theorem is the law of cosines, which allows the computation of the length of any side of any triangle, given the lengths of the other two sides and the angle between them. If the angle between the other sides is a right angle, the law of cosines reduces to the Pythagorean equation.
Which tablet records Pythagorean triples from Babylonian times?
The Plimpton 322 tablet records Pythagorean triples from Babylonian times.
Which theorem relates the cross product and dot product in a similar way?
The Pythagorean theorem relates the cross product and dot product in a similar way:
What is the hypotenuse of the Pythagorean theorem?
The picture below shows the formula for the Pythagorean theorem. For the purposes of the formula, side c ¯ is always the hypotenuse. Remember that this formula only applies to right triangles .
How to solve for hypotenuse?
This problems is like example 1 because we are solving for the hypotenuse . Step 1. Identify the legs and the hypotenuse of the right triangle . The legs have length 14 and 48. The hypotenuse is X. Next step . Step 2. Substitute values into the formula (remember 'C' is the hypotenuse). A 2 + B 2 = C 2 14 2 + 48 2 = x 2.
Why are the legs 6 and 8?
The legs have length 6 and 8. X is the hypotenuse because it is opposite the right angle.
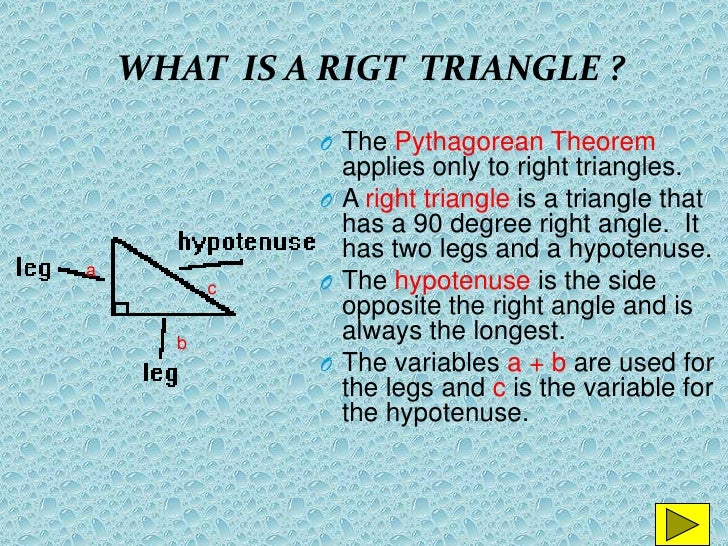
What is the Pythagorean Theorem?
The Pythagorean Theorem states that the sum of the squared sides of a right triangle equals the length of the hypotenuse squared.
What is the smallest Pythagorean triple?
The smallest known Pythagorean triple is 3, 4, and 5. Showing the work:
What is the side of the triangle opposite the right angle?
This calculator solves the Pythagorean Theorem equation for sides a or b, or the hypotenuse c. The hypotenuse is the side of the triangle opposite the right angle.

Overview
In mathematics, the Pythagorean theorem, or Pythagoras' theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the leng…
Other forms of the theorem
If c denotes the length of the hypotenuse and a and b denote the two lengths of the legs of a right triangle, then the Pythagorean theorem can be expressed as the Pythagorean equation:
If only the lengths of the legs of the right triangle are known but not the hypotenuse, then the length of the hypotenuse can be calculated with the equation
If the length of the hypotenuse and of one leg is known, then the length of the other leg can be c…
Proofs using constructed squares
In one rearrangement proof, two squares are used whose sides have a measure of and which contain four right triangle whose sides are a, b and c, with c being the hypotenuse. In the first square, the triangles are placed such that the corners of the square correspond to the corners of the right angle in the triangles, forming a square in the center whose sides are length c. Each square has an area of both and , with representing the area of the four triangles. In the second sq…
Other proofs of the theorem
This theorem may have more known proofs than any other (the law of quadratic reciprocity being another contender for that distinction); the book The Pythagorean Proposition contains 370 proofs.
This proof is based on the proportionality of the sides of three similar triangles, that is, upon the fact that the ratio of any two corresponding sides of similar tri…
Converse
The converse of the theorem is also true:
For any three positive numbers a, b, and c such that a + b = c , there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides of lengths a and b.
An alternative statement is:
For any triangle with sides a, b, c, if a + b = c , then the angle between a and b measures 90°.
Consequences and uses of the theorem
A Pythagorean triple has three positive integers a, b, and c, such that a + b = c . In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths. Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).
A primitive Pythagorean triple is one in which a, b and c are coprime (the greate…
Generalizations
The Pythagorean theorem generalizes beyond the areas of squares on the three sides to any similar figures. This was known by Hippocrates of Chios in the 5th century BC, and was included by Euclid in his Elements:
If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of t…
History
There is debate whether the Pythagorean theorem was discovered once, or many times in many places, and the date of first discovery is uncertain, as is the date of the first proof. Historians of Mesopotamian mathematics have concluded that the Pythagorean rule was in widespread use during the Old Babylonian period (20th to 16th centuries BC), over a thousand years before Pythagoras …