In order to apply the central limit theorem, there are four conditions that must be met:
- Randomization: The data must be sampled randomly such that every member in a population has an equal probability of being selected to be in the sample.
- Independence: The sample values must be independent of each other.
- The 10% Condition: When the sample is drawn without replacement, the sample size should be no larger than 10% of the population.
- Large Sample Condition: The sample size needs to be sufficiently large.
How do you calculate the central limit theorem?
μ = E ( X i) = r = 3. while the variance of a chi-square random variable with three degrees of freedom is: σ 2 = V a r ( X i) = 2 r = 2 ( 3) = 6. The Central Limit Theorem, therefore, tells us that the sample mean X ¯ is approximately normally distributed with mean: μ X ¯ = μ = 3. and variance: σ X ¯ 2 = σ 2 n = 6 n.
What does the central limit theorem require?
when using the central limit theorem, if the original variable is not normal, a sample size of 30 or more is needed to use a normal distribution to the approximate the distribution of the sample means. The larger the sample, the better the approximation will be. The formula, z= x̄ -μ / (σ/√n) is used to gain information about a sample mean
What does the central limit theorem enable researchers to do?
The central limit theorem tells us exactly what the shape of the distribution of means will be when we draw repeated samples from a given population. Specifically, as the sample sizes get larger, the distribution of means calculated from repeated sampling will approach normality.
How to understand the central limit theorem?
What is the Central Limit Theorem?
- To begin, select groups of students from the class at random. ...
- Calculate each sample's individual mean.
- Calculate the average of these sample means.
- The value will give us the approximate average marks of the students in Class X.
- The histogram of the sample means marks of the students will resemble a bell curve or normal distribution.

Under what conditions can we use the central limit theorem for means?
The central limit theorem states that the sampling distribution of the mean will always follow a normal distribution under the following conditions: The sample size is sufficiently large. This condition is usually met if the sample size is n ≥ 30.
When can you apply the central limit theorem?
It is important for you to understand when to use the central limit theorem. If you are being asked to find the probability of the mean, use the clt for the mean. If you are being asked to find the probability of a sum or total, use the clt for sums. This also applies to percentiles for means and sums.
How do you know if central limit theorem is met?
In order to apply the central limit theorem, there are four conditions that must be met:Randomization: The data must be sampled randomly such that every member in a population has an equal probability of being selected to be in the sample.Independence: The sample values must be independent of each other.More items...•
What must be true to use the central limit theorem?
Sample size equal to or greater than 30 are required for the central limit theorem to hold true. A sufficiently large sample can predict the parameters of a population such as the mean and standard deviation.
What does the central limit theorem require quizlet?
The central limit theorem states that the sampling distribution of any statistic will be normal or nearly normal, if the sample size is large enough.
What is the central limit theorem when does it apply quizlet?
Central Limit Theorem (CLT) tells us that for any population distribution, if we draw many samples of a large size, nn, then the distribution of sample means, called the sampling distribution, will: Be normally distributed.
What are the 3 conditions of central limit theorem?
It must be sampled randomly. Samples should be independent of each other. One sample should not influence the other samples. Sample size should be not more than 10% of the population when sampling is done without replacement.
What are the three properties of central limit theorem?
To wrap up, there are three different components of the central limit theorem: Successive sampling from a population. Increasing sample size. Population distribution....Understanding the central limit theoremµ is the population mean.σ is the population standard deviation.n is the sample size.
Which of the following conditions regarding sample size must be met to apply the central limit theorem for sample proportions?
Which of the following conditions regarding sample size must be met to apply the Central Limit Theorem for Sample Proportions? To apply the Central Limit Theorem for Sample Proportions the sample size must be large enough that the sample expects at least 10 successes and 10 failures.
Which of the following is false about the central limit theorem?
It is false. The correct statement is: The central limit theorem states that if you have a population with mean and standard deviation and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. Thus, D is false.
What conditions are required by the central limit theorem before a confidence interval of the population mean may be created?
What conditions are required by the central limit theorem before a confidence interval of the population mean may be created? The underlying population need not be normally distributed if the sample size is 30 or more.
What conditions must be met for a sampling distribution to be normal?
Normal: The sampling distribution of p^p, with, hat, on top needs to be approximately normal — needs at least 10 expected successes and 10 expected failures. Independent: Individual observations need to be independent. If sampling without replacement, our sample size shouldn't be more than 10% of the population.
Does the central limit theorem apply to discrete random variables?
The central limit theorem can be applied to both discrete and continuous random variables.
Does central limit theorem apply median?
Answer and Explanation: No. The central limit theorem states that for any distribution, with mean μ and standard deviation σ , the sampling distribution will tend towards a normal distribution also with mean μ , and standard deviation equal to σ/√n as the sample size n grows towards infinity.
Does central limit theorem apply to variance?
The central limit theorem applies to almost all types of probability distributions, but there are exceptions. For example, the population must have a finite variance. That restriction rules out the Cauchy distribution because it has infinite variance.
How many failures are expected in the Central Limit Theorem?
To apply the Central Limit Theorem for Sample Proportions the sample size must be large enough that the sample expects at least 10 successes and 10 failures.
What is the probability that a sample proportion will fall within 2 standard errors of the population proportion?
The probability that a sample proportion will fall within 2 standard errors of the population proportion is 95%.
How big must a population be to be considered a sample?
The population size must be at least 10 times bigger than the sample size.
Why should the z score be less than 50%?
The answer should be less than 50%, because the resulting z-score will be negative and the sampling distribution is approximately Normal. A. The answer should be greater than 50%, because 0.5 is less than the population proportion of 0.55 and because the sampling distribution is approximately Normal.
Can standard error be computed if the value for p is unknown?
D. None of these. The standard error cannot be computed if the value for p is unknown.
How to find the central limit theorem?
1. Check the Central limit theorem conditions for sample means: 1 The sample data must be independent. The data are randomly sampled from the population so they are independent. 2 The sample size must be sufficiently large. The sample size = 30 so it is large according to the CLT.
How many standard deviations are there in a normal distribution?
For any normal distribution, 95% of the data are within 2 (or more accurately 1.96) standard deviations from the mean.
What is the sample size of a CLT?
The sample size (n) is at least 30 to apply the CLT to sample means and the sampling distribution of the sample mean will be nearly normal, even if the underlying population distribution of individual observations is not normally distributed.
When is the sample size sufficiently large?
The sample size (n) is sufficiently large if np ≥ 10 and n (1-p) ≥ 10. p is the population proportion.
What is the x axis of a histogram?
The x-axis is the individual incomes and the histogram has a right-skewed distribution and not centered around the population mean which is plotted as a vertical black line.

What Is The Central Limit Theorem?
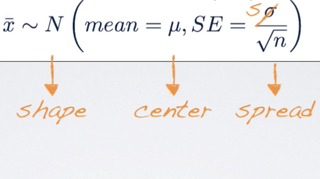
Central Limit Theorem Formula
- Fortunately, you don’t need to actually repeatedly sample a population to know the shape of the sampling distribution. The parametersof the sampling distribution of the mean are determined by the parameters of the population: 1. The meanof the sampling distribution is the mean of the population. 1. The standard deviationof the sampling distribution is the standard deviation of the …
Sample Size and The Central Limit Theorem
- The sample size (n) is the number of observations drawn from the population for each sample. The sample size is the same for all samples. The sample size affects the sampling distribution of the mean in two ways.
Conditions of The Central Limit Theorem
- The central limit theorem states that the sampling distribution of the mean will always follow a normal distributionunder the following conditions: 1. The sample size is sufficiently large. This condition is usually met if the sample size is n ≥ 30. 1. The samples are independent and identically distributed (i.i.d.) random variables. This condition...
Importance of The Central Limit Theorem
- The central limit theorem is one of the most fundamental statistical theorems. In fact, the “central” in “central limit theorem” refers to the importance of the theorem. The implication of the central limit theorem is that statistical theories that apply to normal distributions.
Central Limit Theorem Examples
- Applying the central limit theorem to real distributions may help you to better understand how it works.