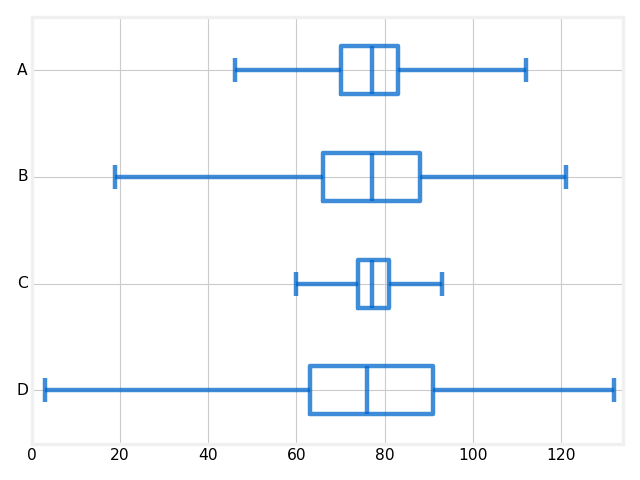
Which set has the smallest standard deviation?
It is graphically clear that the data values in Set C are close to the mean and that is why this set has the smallest standard deviation. The graphs on the number line of set A and B shows that data in Set A is more dispersed than the data in set B, hence the standard deviation is set A is larger than of set B.
What is the standard deviation?
The standard deviation is a measure of how close the data values in a data set are from the mean. It is a quantity that is small when data is distributed close to the mean and large when data is far form the mean.
Why do the two sets have the same standard deviations?
This means the data values in the two sets are distributed in the same way around the mean. The two sets A and B are shown below on number lines. Although the two sets are different, the distances between the data values and the mean are correspondingly equal and that explains why the two sets have equal standard deviations.
Why do we use n-1 in standard deviation for samples?
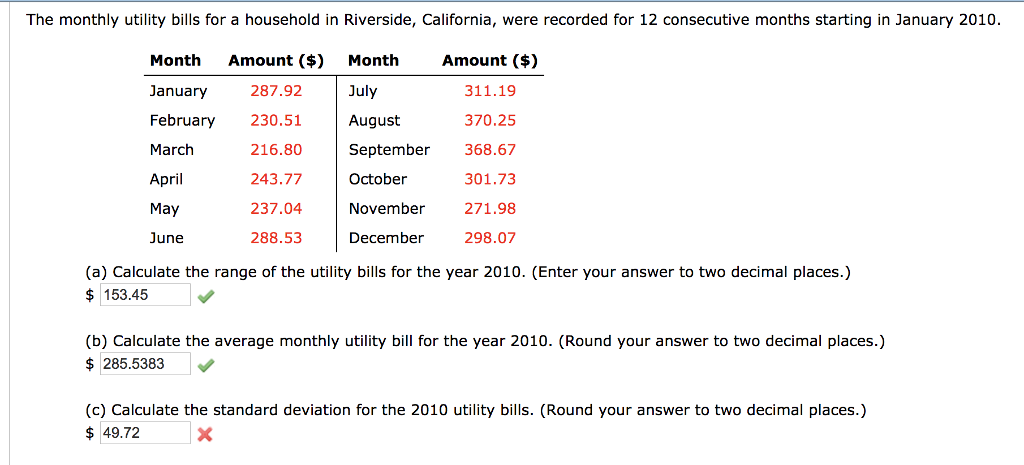
We use N - 1 in the formula of the standard deviation for samples to compensate for the fact that the number of data values in a population is much larger than the number of data values in a sample. Note also that for N very large, the two formulas would give very close values.

How do you find the largest standard deviation?
Step 1: Find the mean. Step 2: For each data point, find the square of its distance to the mean. Step 3: Sum the values from Step 2. Step 4: Divide by the number of data points.
Which of the following statements about a standard deviation is true?
Answer: B - The true statement about standard deviation is that 2/3 of the values in a normal data distribution lie within one standard deviation from the mean. Standard deviation is a statistical measure that shows the degree of variation from the mean in a distribution.
What does it mean when the standard deviation is 0?
identicalIf all of the values in the sample are identical, the sample standard deviation will be zero.
Does the standard deviation have to be less than the mean?
In practice, the SD value should always be smaller than the mean. However, there is no statistical significance of the SD being greater than the mean: 1. If there are both negative and positive values in the distribution.
Which of the following statements is true about the relation between standard deviation and variance?
The variance is equal to the square of standard deviation or the standard deviation is the square root of the variance.
What is standard deviation statistics?
The standard deviation is the average amount of variability in your dataset. It tells you, on average, how far each value lies from the mean. A high standard deviation means that values are generally far from the mean, while a low standard deviation indicates that values are clustered close to the mean.
How does the standard deviation measure the variability of scores?
The standard deviation is the most commonly used and the most important measure of variability. Standard deviation uses the mean of the distribution as a reference point and measures variability by considering the distance between each score and the mean.
Can a standard deviation be negative?
The minimum standard deviation possible is zero. The standard deviation from the minimum feasible value should be zero. If you are not approximately equal to at least two figures in your data set, the standard deviation must be higher than 0 – positive. Standard deviation cannot be negative in any conditions.
What is the smallest standard deviation?
The smallest standard deviation possible in a distribution is 0. This occurs when each element of the distribution is the same.
What is standard deviation when the outcomes are constant?
Standard Deviation = 0 when the outcomes are constant. Consider a two-headed coin. Flip the coin. The outcome is always heads.
When all observations are only 0,0,0,0,0 then also mean and variance both will be equal to answer?
when all observations are only 0,0,0,0,0 then also mean and variance both will be equal to 0.
What is the mnemonic for "sum of the squares minus square of the sum divided by N?
The mnemonic is “Sum of the squares minus square of the sum divided by N will get it done.”
Why are the mean and standard deviation equal?
The means are different and the standard deviation are equal. This means the data values in the two sets are distributed in the same way around the mean. The two sets A and B are shown below on number lines. Although the two sets are different, the distances between the data values and the mean are correspondingly equal and that explains why the two sets have equal standard deviations.
Why does the standard deviation of a number line not change?
However the standard deviation will not change because it is a measure of the distance between the data values and the mean and they all shifted by the same value k.