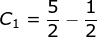
How do I make an equation to be dimensionally consistent?
a · t → ( m / s 2) ⋅ ( s) = m s 2 ⋅ s = m / s, so all is well; all three summands in the equation, v, v0, a·t, have the same units, so that the equation is “dimensionally consistent.” (Physical units are also called “dimensions” …I know, it can be confusing… but it beats saying “unitally consistent” :-) 9.
Is the linear pair of equations always consistent?
There will be a unique solution to the pair of linear equations if both the lines intersect at a point. Here, the pair of linear equations is said to be consistent. In the graph shown above, lines intersect at point P (x,y) which represents the unique solution of the system of linear equations in two variables.
What does consistent mean in math?
In mathematics and particularly in algebra, a linear or nonlinear system of equations is called consistent if there is at least one set of values for the unknowns that satisfies each equation in the system—that is, when substituted into each of the equations, they make each equation hold true as an identity.
Are linear equation systems consistent or inconsistent?
Linear equation: A linear equation is an equation of two variables (commonly x and y) which contains no exponents on the variables other than 1. Consistent systems: A system of equations is consistent if it has at least one solution. If it has no solutions, it is inconsistent.
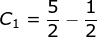
How do you know if an equation is consistent?
A consistent system of equations is one that has at least one solution. If you have the system: {x+y=102x+2y=20 { x + y = 10 2 x + 2 y = 20 That's consistent, because the solutions are the line x+y=10 x + y = 10 .
How do you find if an equation is consistent or inconsistent?
If a consistent system has exactly one solution, it is independent . If a consistent system has an infinite number of solutions, it is dependent . When you graph the equations, both equations represent the same line. If a system has no solution, it is said to be inconsistent .
What is an example of a consistent equation?
Consistent Meaning In Maths Let's take an example of consistent equations as x + y = 6 and x – y = 2 there is one solution in common. Similarly, in the equations x + y = 12 and 3y = x there is also one solution in common hence we can call them consistent equations.
Which system of equations is inconsistent?
That means that the system of equations they represent has no solution. A system with no solutions is called an inconsistent system.
What is consistent or inconsistent in maths?
We consider a system to be consistent if it has at least one solution. A consistent system is independent if it has precisely one solution. When a system does not have a solution, we say it to be inconsistent. Because the line graphs do not meet, the graphs are parallel; thus, there is no solution.
What is meant by consistent and inconsistent?
If atleast one set of values occurred for the unknowns that satisfies every equation in the system, then that system of equations is known as consistent. If no set of values satisfies the equation, then that system is known as inconsistent. Solve any question of Pair of Linear equations with:- Patterns of problems.
What is an example of a consistent system?
Consistent systems have at least one solution in common. For example, the equations x + y = 6 and x – y = 2 have one solution in common, the ordered pair (4, 2) because 4 + 2 equals 6 and 4 – 2 equals 2.
What is an example of an inconsistent equation?
Inconsistent-equations definition Inconsistent equations is defined as two or more equations that are impossible to solve based on using one set of values for the variables. An example of a set of inconsistent equations is x+2=4 and x+2=6.
How do you prove inconsistent?
A theory is inconsistent if we can prove a contradiction using basic logic and the principles of that theory. Consistency is a much weaker condition that truth: if a theory T is true, then T consistent, since a true theory only allows us to prove true claims, and contradictions are not true.
Is parallel lines consistent?
Definitions: If the two equations describe lines that intersect once, the system is independent and consistent. If the two equations describe parallel lines, and thus lines that do not intersect, the system is independent and inconsistent.
What is a consistent dependent?
Consistent Dependent: A system of linear equations is consistent dependent if it has an infinite number of solutions. When this is the case, the graphs of the lines in the system are the same, meaning the equations in the system represent the same line.
What does it mean when 2 lines are consistent?
A system with exactly one solution is called a consistent system. To identify a system as consistent, inconsistent, or dependent, we can graph the two lines on the same graph and see if they intersect, are parallel, or are the same line.
Are parallel lines consistent or inconsistent?
Definitions: If the two equations describe lines that intersect once, the system is independent and consistent. If the two equations describe parallel lines, and thus lines that do not intersect, the system is independent and inconsistent.
Are coincident lines consistent or inconsistent?
If the pair of lines are coincident, then we say that pair is consistent and it has a unique solution.
What is consistent in math?
In mathematics and particularly. in algebra, a linear or nonlinear system of equations is called consistent if there is at least one set of values for the unknowns that satisfies each equation in the system—that is, when substituted into each of the equations, they make each equation hold true as an identity. ...
How to find inconsistency of an equation?
has no solutions; the inconsistency can be seen by multiplying the first equation by 4 and subtracting the second equation to obtain the impossible 0 = 2.
Why is the last equation inconsistent?
is inconsistent because the last equation contradicts the information embedded in the first two, as seen by multiplying each of the first two through by 2 and summing them.
Why does the third equation have infinite solutions?
has an infinite number of solutions because the third equation is the first equation plus twice the second one and hence contains no independent information; thus any value of z can be chosen and values of x and y can be found to satisfy the first two (and hence the third) equations.
Is a linear system consistent?
A linear system is consistent if and only if its coefficient matrix has the same rank as does its augmented matrix (the coefficient matrix with an extra column added, that column being the column vector of constants).
What is inconsistent system?
Inconsistent System. Let both the lines to be parallel to each other, then there exists no solution, because the lines never intersect. Algebraically, for such a case, = ≠ and the pair of linear equations in two variables is said to be inconsistent.
Do lines coincide with each other?
Therefore, we can say that the lines coincide with each other, having an infinite number of solutions.
Is a pair of linear equations dependent and consistent?
In such a case, the pair of linear equations is said to be dependent and consistent. As represented in the graph below, the pair of lines coincides and therefore, dependent and consistent.
What is a consistent system of equations?
A consistent system of equations is one that has at least one solution. If you have the system:
What does it mean when a system of equations has no solutions?
If a system of equations has no solutions, then it is inconsistent. If the last column (in an augmented matrix) is a pivot column, that is, it has a pivot, then it's inconsistent.
What is the equation for the fifth column of a pivot column?
This requires two steps. If the last column is a pivot column, then that row gives an equation that looks something like 0x + 0y + 0z = 1, meaning 0 = 1.
How to determine if a variable is basic or free?
It isn't bound by any equation. So, to determine whether a variable is basic or free, check whether it has a pivot value. In the matrix above, the first, second, and third columns were pivot columns, meaning those three variables were basic, while the fourth was free.
What is a basic variable?
A basic variable is one that is bound by an equation. A free variable is not bound by any equation. Here is an example:
How many lines are consistent?
Then you can say that a consistent system (with at least 2 lines) has one solution or infinite solutions.
What is the difference between a consistent system and an inconsistent system?
A consistent system of equations has at least one solution, and an inconsistent system has no solution. Watch an example of analyzing a system to see if it's consistent or inconsistent.
How to solve a system with three variables?
To solve a system with three variable you need three equations. Combine them in two sets of two to get rid of one variable. Then combine these two equations to get rid of another variable. Comment on Theresa Johnson's post “To solve a system with th...”.
Why is it called inconsistent?
more. "Inconsistent" is because it is not possible for both equations to hold simultaneously. They contradict each other in the sense that if one holds, the other must fail. Thus their graphs never intersect and there is no solution to their system. "Consistent" is then the opposite.
Do lines cross if the system includes other degrees?
Direct link to doctorfoxphd's post “Yes, if the system includ...”. Yes, if the system includes other degrees (exponents) of the variables, but if you are talking about a system of linear equations, the lines can either cross, run parallel or coincide because linear equations represent lines.
Can a single equation be inconsistent?
That is not a system of equations, so a single equation cannot be inconsistent, it is just a linear equation. If you had 2x - 2y = 14 as a second equation, then the two would be inconsistent.
How to prove that a linear equation is consistent?
Solution: In order to prove that a given system of linear equations is consistent, you must show that the ranks of the coefficient matrix as well as the corresponding augmented matrix associated with the given system are the same. The easiest way to establish this is to reduce the augmented matrix to a row-echelon form by using elementary row operations on it. It is to be noted that a homogeneous system of equations, i.e. in where the RHS of the equations are equal to 0, is always consistent.
What are the conditions for a two variable system of linear equations to be considered consistent?
If the lines formed by the equation meet at some point or are parallel then a two-variable system of equations to be considered consistent. If a three-variable system of consistent linear equations is to be considered to be true then it must meet the following conditions: All the three planes will have to parallel.
What Does Inconsistent Systems Mean?
Inconsistent equations of linear equations are equations that have no solutions in common. In this system, the lines will be parallel if the equations are graphed on a coordinate plane. Let's consider an inconsistent equations as x – y = 8 and 5x – 5y = 25. They don’t have any common solutions.
How many solutions can a two variable system of equations have?
A two-variable system of equations is considered as equations of two lines and they can have infinitely many solutions if these two lines are parallel where they can be expressed as multiples of each other. This is a quick way to spot systems with infinitely many solutions.
Why do we end up with an equation that makes no sense mathematically?
Often we attempt to solve that system but end up with an equation that makes no sense mathematically because these equations are empty of any acceptable solution. Like for example,
What is a system of linear equations?
System of linear equations is a group of two or more linear equations having the same variables. For example, x + 2y = 14 , 2x + y = 6.
What is the elimination method?
In order to solve the variable in a system of equations, elimination method is used to eliminate the remaining variables. This elimination method is also known as elimination by addition. So, to find the correct value for the other variable it is substituted to the original equation after the values for the remaining variables are found.
What is dependent equation?
If the two lines share all points in common, then the lines are said to be dependent. Dependent equations intersect at all points. These lines look as if they are lying on top of each other. All the points on both lines will make both equations true.
How to graph a linear equation?
Since the graphing of all three possibilities depends on knowing the slope and y -intercept; putting the equations in the y = mx + b form would be the simplest approach. You will need to move the parts of the equation until you have y isolated on one side of the equation. If the equation is in the form of y = mx + b; then the point (0,b) is the y-intercept and the m is the slope, which tells you how to move from the y -intercept when graphing.
What are the three possible possibilities when you graph two equations onto the same coordinate grid?
When you graph two equations onto to the same x,y coordinate grid, you only have three possibilities. One possibility is that the lines will intersect at one point. A second possibility is that they never intersect and the final possibility is that they have all points in common; they intersect at every point.
What are the three different possibilities when graphing linear equations?
If you were to graph these runners on a grid with seconds on the x -axis and meters on the y -axis, Race 1, 2, and 3 would show you the three different possibilities when graphing linear equations. Race 1 demonstrates a consistent graphing. Race 2 shows a inconsistent graphing. Race 3 is the dependent graphing. This lesson will define the different possibilities and instruct you on how to graph them.
What happens when two linear equations are graphed on the x-y coordinate grid?
When two linear equations are graphed on the x,y coordinate grid, you have three possible results. The two equations can be consistent, inconsistent, or dependent. This lesson explains how to graph these equations and what the graphs mean.
How far ahead is Josh in Race 2?
Race 2: This time Josh gives Will a 20 meter head-start. They both run a consistent 7 meter s per second. The entire race Will is exactly 20 meters ahead of Josh. Josh never gets any closer.
How many races are Josh and Will running?
Josh and Will are running three 500 meter races against each other. Each race has a different outcome.
