Key Terms
- Independent system: A system of equations with a single solution. For systems of equations in three variables, this solution is an ordered triple (x,y,z) ( x, y, z) that represents ...
- Dependent system: A system of equations with an infinite number of solutions. ...
- Inconsistent system: A system of equations with no solution. ...
How do I solve the system of equatons?
Method 2 Method 2 of 4: Solve by Addition Download Article
- Write one equation above the other. Solving a system of equations by addition is ideal when you see that both equations have one variable with the same coefficient with ...
- Add like terms. Now that you've lined up the two equations, all you have to do is add the like terms.
- Solve for the remaining term. ...
What are the possible solutions for system of equations?
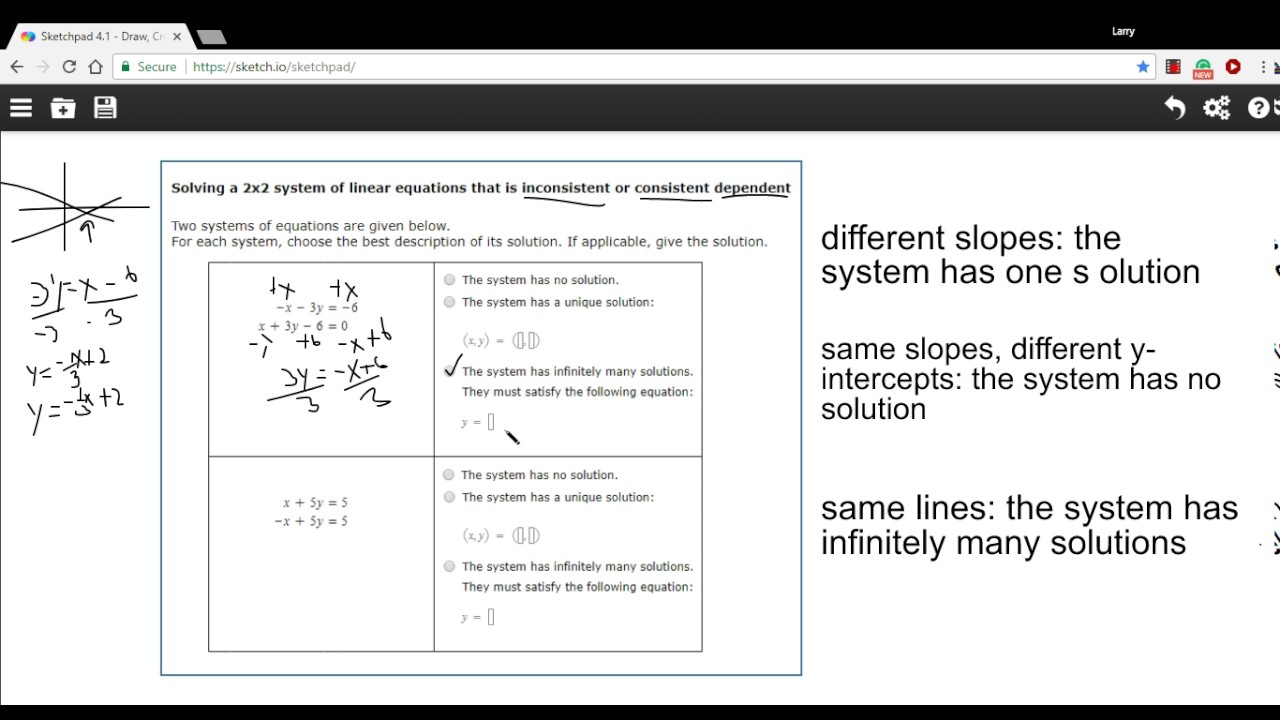
What are the possible solutions to a system of equations? 1) graphing, 2) substitution, and 3) elimination (or adding). There are three possible solutions to a system of equations: First, if the lines have different slopes then they will have one solution. The lines when graphed will intersect in one point.
Which graph represents an inconsistent system?
o When a system has one solution (the graphs of the equations intersect once), the system is a consistent system of linear equations and the equations are independent. o When a system has no solution (the graphs of the equations don’t intersect at all), the system is an inconsistent system of linear equations and the equations are independent.
Is X,Y solution to the system of equations?
Similarly, for a system of linear equations in two variables, the unique solution is an ordered pair (x, y) which will satisfy both the equations in the system. A system of equations has no solution when there exists no point where lines intersect each other or the graphs of equations are parallel.

How do you know if a system of equations is inconsistent?
A consistent system of equations has at least one solution, and an inconsistent system has no solution.
What type of system is inconsistent?
Inconsistent Systems When graphed, the lines will have the same steepness with different intercepts. Therefore, parallel lines will never intersect, so they have no solution. A system with no solutions is called an inconsistent system.
What is example of inconsistent equations?
Inconsistent-equations definition Inconsistent equations is defined as two or more equations that are impossible to solve based on using one set of values for the variables. An example of a set of inconsistent equations is x+2=4 and x+2=6.
What is an example of an inconsistent system?
In other words, no two numbers exist such that 5 times the first number added to 2 gives the second number, and if you subtract 2 times the second number from 10 times the first number, you get 12. Zero can't equal 16, so the statement 0 = 16 makes no sense. Therefore, the system is inconsistent and has no solution.
How do you know if a system is consistent or independent?
0:365:37Consistent Independent, Dependent and Inconsistent - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd these are called consistent. But when there's one solution this is called consistent independentMoreAnd these are called consistent. But when there's one solution this is called consistent independent okay and when there's an infinite solution where they're the same line like that that's called
What is an inconsistent solution set?
A solution set can have a finite number of solutions, an infinite number of solutions, or no solution. When the system has no solution, we say that the system is inconsistent. We can identify an inconsistent system graphically when the graphs of the equations in the system don't intersect.
What is an example of a consistent system?
Consistent systems have at least one solution in common. For example, the equations x + y = 6 and x – y = 2 have one solution in common, the ordered pair (4, 2) because 4 + 2 equals 6 and 4 – 2 equals 2.
What makes a system of equations consistent?
In mathematics and particularly in algebra, a linear or nonlinear system of equations is called consistent if there is at least one set of values for the unknowns that satisfies each equation in the system—that is, when substituted into each of the equations, they make each equation hold true as an identity.
How do you solve a consistent and inconsistent system?
0:285:28Consistent and inconsistent systems | Algebra II | Khan Academy - YouTubeYouTubeStart of suggested clipEnd of suggested clipSystem another consistent system would be if they're the same line because then they would intersectMoreSystem another consistent system would be if they're the same line because then they would intersect. They would intersect at a ton of points actually an infinite number of points.
How do you make an equation inconsistent?
Inconsistent System Let both the lines to be parallel to each other, then there exists no solution because the lines never intersect. Algebraically, for such a case, a1/a2 = b1/b2 ≠ c1/c2, and the pair of linear equations in two variables is said to be inconsistent.
What do you mean by inconsistent in mathematics?
Inconsistent mathematics is the study of the mathematical theories that result when classical mathematical axioms are asserted within the framework of a (non-classical) logic which can tolerate the presence of a contradiction without turning every sentence into a theorem.
What is meant by consistent and inconsistent?
If atleast one set of values occurred for the unknowns that satisfies every equation in the system, then that system of equations is known as consistent. If no set of values satisfies the equation, then that system is known as inconsistent. Solve any question of Pair of Linear equations with:- Patterns of problems.
When can a system be inconsistent?
Inconsistent System Let both the lines to be parallel to each other, then there exists no solution because the lines never intersect. Algebraically, for such a case, a1/a2 = b1/b2 ≠ c1/c2, and the pair of linear equations in two variables is said to be inconsistent.
What is the meaning of inconsistent system?
A system of equations is called an inconsistent system of equations if there is no solution because the lines are parallel. A dependent system of equations is when the same line is written in two different forms so that there are infinite solutions.
What is a consistent and dependent system?
An ordered pair that satisfies all of the equations in a system is a solution to the system. Linear systems of equations can have one solution, no solution, or infinitely many solutions. Consistent Dependent: A system of linear equations is consistent dependent if it has an infinite number of solutions.
When a linear system is consistent?
A linear system is consistent if and only if its coefficient matrix has the same rank as does its augmented matrix (the coefficient matrix with an extra column added, that column being the column vector of constants).
What does it mean when a system is inconsistent?
Logically, if we can manipulate the equations so that they all have one side in common, we can look at the other side; if the other side differs, then the system is inconsistent. Algebraically, we will run into a contradiction as we are solving the system, indicating that the system is inconsistent.
What is a system of equations?
A system of equations is a group of equations with the same variables. For example, consider the following system of equations: This is a system of equations in two variables, namely x and y. As we know, an equation represents a set of points on a graph.
What is finite number of solutions?
1.) A finite number of solutions: the equations intersect at a finite number of points. Our example above is an example of this - the equations intersect at exactly one point.
How to identify an inconsistent system?
Another way to identify an inconsistent system is by trying to solve the system algebraically. As you're going through the process of solving the system, you will run into a contradiction. That is, you will run into something that doesn't make sense, such as 1 = 2 or 0 = 5.
What is a solution set?
A solution set is the set of all the intersection points of the equations in the system. A solution set can have a finite number of solutions, an infinite number of solutions, or no solution. When the system has no solution, we say that the system is inconsistent.
Can a system of equations be represented graphically?
Therefore, a system of equations can be represented graphically as well as algebraically. The solution set of a system of equations consists of all the points of intersection of the equations in the system. These points represent values we can plug in for the variables to make all of the equations true. For example, we see that the solution of the ...
Why is an equation inconsistent?
An equation is said to be inconsistent if it creates a contradiction. For example, the equation 0 = 1 is inconsistent because 0 and 1 do not have the same value.
What does it mean when a system is inconsistent?
This can be shown either graphically or algebraically. Graphically, if the equations never intersect, then the system is inconsistent. Algebraically, if the system reduces to a statement such as a = b when a and b are different numbers, then the system is inconsistent.
What happens if the equations have a different y intercept?
If the equations have a different y-intercept, then the system is inconsistent
What is inconsistent linear system?
A linear system is said to be inconsistent if there is no point that both lines have in common. This can be seen visually with any two lines that do not intersect such as:
What is a system of equations?
System of equations: A set of two or more equations involving the same variables for which solutions are sought.
Can algebraic simplification be used to identify if a system is inconsistent?
In this case, algebraic simplification can occur to identify if the system is inconsistent. Consider the inconsistent system example shown below:
Why are inconsistent systems of equations referred to as such?
should exist as well, and they do. Inconsistent Systems of Equations are referred. to as such because for a given set of variables, there in no set of solutions for. the system of equations. Inconsistent systems arise when the lines or planes formed from the systems of equations.
What is a consistent system of equations?
These are referred to as Consistent Systems of Equations, meaning that. the system or infinitely many sets of solution. In other words, as long as we can. equations have to meet at some point or they have to be parallel. at some point and the other at another point. should exist as well, and they do.
What happens when three variables of equations have no solution?
Three variable systems of equations with no solution arise when the planed formed#N#by the equations in the system neither meet at point nor are they parallel. As a#N#result, when solving these systems, we end up with equations that make no mathematical#N#sense.
How to make a three variable system of equations consistent?
For a three variable system of equations to be consistent, the equations formed. by the equations must meet two conditions: All three planes have to parallel. Any two of the planes have to be parallel and the third must meet one of the planes. at some point and the other at another point.
What are the three systems of equations with infinitely many solution sets called?
Three variable systems of equations#N#with infinitely many solution sets are also called consistent.
What does it mean to have two sides of an equation?
both sides of the equations. This means that two of the planes formed by the equations. in the system of equations are parallel, and thus the system of equations is said. to have an infinite set of solutions. We solve for any of the set by assigning one.
What is a three variable system of equations?
with infinitely many solution sets are also called consistent. Since the equations in a three variable system of equations are linear, they can. also be thought of as equations of planes. The way these planes interact with each.
Consistent and Inconsistent Equations
A system of equations that is consistent has at least one solution. If you have the system, you can do the following:
Dependent System
We know from dealing with two-variable systems of equations that a dependent system of equations has an unlimited number of solutions. The same holds true for three-variable dependent systems of equations. Several scenarios can lead to an unlimited number of solutions.
Basic and Free Variables
A fundamental variable is one that is restricted by an equation. A free variable is one that is not constrained by any equation. Here's an illustration:
Elimination Technique
Elimination technique is used to remove the remaining variables in order to solve the variable in a system of equations. This method of elimination is also known as elimination by addition. So, after finding the values for the other variables, the right value for the other variable is swapped into the original equation.
Things to Remember
Inconsistency in a three-variable system of equations, which indicates it lacks a solution that satisfies all three equations.
Sample Questions
Ques. What is the solution set to an inconsistency in an equation system? (2 Marks)
What is the difference between a consistent system and an inconsistent system?
A consistent system of equations has at least one solution, and an inconsistent system has no solution. Watch an example of analyzing a system to see if it's consistent or inconsistent.
Why is it called inconsistent?
more. "Inconsistent" is because it is not possible for both equations to hold simultaneously. They contradict each other in the sense that if one holds, the other must fail. Thus their graphs never intersect and there is no solution to their system. "Consistent" is then the opposite.
How to solve a system with three variables?
To solve a system with three variable you need three equations. Combine them in two sets of two to get rid of one variable. Then combine these two equations to get rid of another variable. Comment on Theresa Johnson's post “To solve a system with th...”.
How many lines are consistent?
Then you can say that a consistent system (with at least 2 lines) has one solution or infinite solutions.
Do lines cross if the system includes other degrees?
Direct link to doctorfoxphd's post “Yes, if the system includ...”. Yes, if the system includes other degrees (exponents) of the variables, but if you are talking about a system of linear equations, the lines can either cross, run parallel or coincide because linear equations represent lines.
Can a single equation be inconsistent?
That is not a system of equations, so a single equation cannot be inconsistent, it is just a linear equation. If you had 2x - 2y = 14 as a second equation, then the two would be inconsistent.
What is the difference between a consistent and inconsistent system of equations?
A consistent system of equations is a system that has at least one solution. An inconsistent system of equations is a system that has no solution.
What is a system of equations?
A system of equations is a set of equations that have the same variables. For example, consider the set of the following two equations: This is a system of equations in x and y. The solution set of a system of equations is the set of all values of the variables that make each of the equations in the system true.
Why is a system consistent?
This would be a consistent system because it has at least one solution.
What is the solution set?
The solution set can also be thought of as the set of intersection points on the graphs of the equations in the system. This image shows the graph of our system of equations. Notice their intersection point is (2,4):
What are systems of equations?
The solutions to systems of equations are the variable mappings such that all component equations are satisfied— in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.
What is the solution of a system of equations?
The solutions to systems of equations are the variable mappings such that all component equations are satisfied —in other words, the locations at which all of these equations intersect. To solve a system is to find all such common solutions or points of intersection.

Consistent and Inconsistent Equations
Derivating Inconsistency of Equation
- [Click Here for Sample Questions] The steps to derive the Inconsistent Equation is as follows: Create a matrix equation AX = B from the following system of equations. 1. Step 1: Determine the system of equations' augmented matrix [A, B]. 2. Step 2: Using just basic row operations, determine the rank of A and the rank of [A, B]. Column operations sh...
Dependent System
- [Click Here for Sample Questions] We know from dealing with two-variable systems of equations that a dependent system of equations has an unlimited number of solutions. The same holds true for three-variable dependent systems of equations. Several scenarios can lead to an unlimited number of solutions. Three planes might be the same, therefore the answer to one equation will …
Basic and Free Variables
- [Click Here for Sample Questions] A fundamental variable is one that is restricted by an equation. A free variable is one that is not constrained by any equation. Here's an illustration: Basic and Free Variables Check whether a variable has a pivot value to see if it is basic or free. The first, second, and third columns in the matrix above were pivot columns, indicating that those three variables …
Elimination Technique
- [Click Here for Sample Questions] Elimination technique is used to remove the remaining variables in order to solve the variable in a system of equations. This method of elimination is also known as elimination by addition. So, after finding the values for the other variables, the right value for the other variable is swapped into the original equation. The steps of the Elimination M…
Things to Remember
- [Click Here for Sample Questions] 1. Inconsistency in a three-variable system of equations, which indicates it lacks a solution that satisfies all three equations. 2. Equations might represent three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect but not at the same point as the other two. 3. A linear system is consistent if and only if its coefficie…