
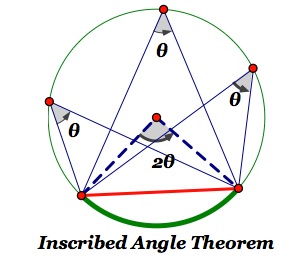
Why are inscribed angles half the arc? The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.
What is the measure of the inscribed angle of the arc?
The inscribed angle's measure is half that of the central angle of the same arc, as we will now prove. This will be a long proof, as it needs to address several different cases - so fasten your seat belt! Show that an inscribed angle's measure is half of that of a central angle that subtends, or forms, the same arc.
What inscribed angle measures half of a semi-circle?
In a semi-circle, the intercepted arc measures 180 ° and therefore any corresponding inscribed angle would measure half of it.
What happens when an inscribed angle and a central angle intercept?
We're about to prove that something cool happens when an inscribed angle and a central angle intercept the same arc: The measure of the central angle is double the measure of the inscribed angle. To prove for all and (as we defined them above), we must consider three separate cases:
What are the theorems of inscribed angles?
There are two theorems of inscribed angles to remember. The first is that half of the central angle is the inscribed angle. The other is that if the arc lengths are the same, the inscribed angles will always be the same.
Is an inscribed angle half the arc?
Theorem 70: The measure of an inscribed angle in a circle equals half the measure of its intercepted arc.
Are inscribed angles equal to the arc?
The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. Inscribed angles that intercept the same arc are Congruent. This is called the Congruent Inscribed Angles theorem and is shown below.
Are inscribed angles half of central angles?
The inscribed angle theorem is also called the angle at the center theorem as the inscribed angle is half of the central angle. Since the endpoints are fixed, the central angle is always the same no matter where it is on the same arc between the endpoints.
Is an inscribed angle is twice the size of its subtended arc?
The measure of the central angle is equal to twice the measure of the inscribed angle subtended by the same arc. An inscribed angle is half of a central angle that subtends the same arc. The angle at the centre of a circle is twice any angle at the circumference subtended by the same arc.
Why are inscribed angles that intercept the same arc congruent?
Inscribed angles are angles whose vertices are on a circle and that intersect an arc on the circle. The measure of an inscribed angle is half of the measure of the intercepted arc and half the measure of the central angle intersecting the same arc. Inscribed angles that intercept the same arc are congruent.
What is an inscribed angle of a circle that intercepts a semicircle?
Proof: The intercepted arc for an angle inscribed in a semi-circle is 180 degrees. Therefore the measure of the angle must be half of 180, or 90 degrees. In other words, the angle is a right angle.
What is the relationship between inscribed angle and central angle?
The measure of the central angle is the same measure of the intercepted arc. You can see that if a central angle and an inscribed angle intercept the same arc, the central angle would be double the inscribed angles. Likewise, the inscribed angle is half of the central angle.
What is the difference between central angle and inscribed angle of a circle?
Central angle = Angle subtended by an arc of the circle from the center of the circle. Inscribed angle = Angle subtended by an arc of the circle from any point on the circumference of the circle.
When the inscribed angle is between a chord and the diameter of a circle?
Case 1: When the inscribed angle is between a chord and the diameter of a circle: To prove α = 2θ: △ CBD is an isosceles triangle whereby CD = CB = the radius of the circle.
Is the arc double the angle?
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
What happens when two inscribed angles subtended by the same arc?
Inscribed angles subtended by the same arc are equal. If a pair of arcs in the same circle are congruent, their inscribed angles are equal. If a pair of circles are congruent, then inscribed angles subtended by congruent arcs, or arcs of equal measure, will be equal.
Why is the semicircle angle 90?
Angles in a semicircle are 90 degrees: The two points A and B are joined to another point C on the circumference using two chords. This triangle is a right-angle triangle with the 90 degree angle touching the arc. This is the same for any point that is placed on the arc.
What is the relationship between arcs and inscribed angles?
The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. Inscribed angles that intercept the same arc are congruent.
Can two inscribed angles intercept the same arc?
If two inscribed angles intercept the same arc, then the angles are equal.
What is the relationship between the measure of an inscribed angle to the measure of its intercepted?
The measure of an inscribed angle is half the measure of the intercepted arc.
What happens if two inscribed angles intercept the same arc?
1:252:33If two inscribed angles share the same arc how do they relate - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo what i notice is well if both of the arcs are one hat or i'm sorry both of the measures of theseMoreSo what i notice is well if both of the arcs are one hat or i'm sorry both of the measures of these angles. Both of the measures these angles are one half the arc of pq. Then i can say that they are.
What is the measure of an inscribed angle in a circle?
Theorem 70: The measure of an inscribed angle in a circle equals half the measure of its intercepted arc. The following two theorems directly follow from Theorem 70. Theorem 71: If two inscribed angles of a circle intercept the same arc or arcs of equal measure, then the inscribed angles have equal measure.
What is an inscription angle?
Inscribed angle: In a circle, this is an angle formed by two chords with the vertex on the circle. Intercepted arc: Corresponding to an angle, this is the portion of the circle that lies in the interior of the angle together with the endpoints of the arc.
What are the angles that are most often associated with a circle?
Central angles are probably the angles most often associated with a circle, but by no means are they the only ones. Angles may be inscribed in the circumference of the circle or formed by intersecting chords and other lines. Inscribed angle: In a circle, this is an angle formed by two chords with the vertex on the circle.
What is the inscribed angle theorem?
Inscribed angle theorem proof. Proving that an inscribed angle is half of a central angle that subtends the same arc.
What is the radian of an angle?
The radians for an angle are based on how many radii equal the length of the same arc subtended by that angle. In relation to the circumference, the circumference is equal to 2 (pi) (r) r meaning radius, not radians (there is a difference).
How many halves does the diameter split?
In our new diagram, the diameter splits the circle into two halves. Each half has an inscribed angle with a ray on the diameter. This is the same situation as Case A, so we know that
Can rays originate at points?
Yes except the rays cannot originate at the points, they originate at the vertex of the inscribed angle and extend through the points on the circle. Sal talks about it as: inscribed angle is half of a central angle that subtends the same arc. Comment on David Severin's post “Yes except the rays canno...”.
What is the result of the inscribed angle theorem?
An especially interesting result of the Inscribed Angle Theorem is that an angle inscribed in a semi-circle is a right angle. In a semi-circle, the intercepted arc measures 180° and therefore any corresponding inscribed angle would measure half of it.
What is an inscribed angle?
An inscribed angle in a circle is formed by two chords that have a common end point on the circle. This common end point is the vertex of the angle.
What is the result of the Inscribed Angle Theorem?
An interesting result of the Inscribed Angle Theorem is that the only thing that matters is the arc on the perimeter. Any two inscribed angles that subtend that arc are equal.
What is the first inscribed angle?
The first inscribed angle is β1 , and the second inscribed angle is (β+β1). α1 is a central angle that subtends the same arc as β1, so it is equal to 2*β1 (as proven for the first case), and the angle (α1+α) is a central angle that subtends the same arc as (β+β1) so it is equal to 2* (β+β1) (again, as proven for the first case).
What is the angle of a circle called?
If we draw lines from the center of the circle to the end-points of an arc on the perimeter of a circle, (these lines are both radii), we will define an angle called a Central Angle . If we draw chords from a point on the circle perimeter to each of the endpoints of an arc, we will define an angle called an Inscribed Angle.
What is the case of the diameter in a chord?
The first is when one of the chords is the diameter. The second case is where the diameter is in the middle of the inscribed angle. And the third case is when the diameter is outside the inscribed angle . These three cases cover all the possibilities (the diameter is either inside the inscribed angle, outside the inscribed angle, ...
