Right triangles are triangles in which one of the interior angles is 90 degrees, a right angle. Since the three interior angles of a triangle add up to 180degrees, in a right triangle, since one angle is always 90 degrees, the other two must always add up to 90 degrees (they are complementary). Can a triangle be isosceles
Isosceles triangle
In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having two and only two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case.
How do you solve right triangles?
Solving for a side in right triangles with trigonometry
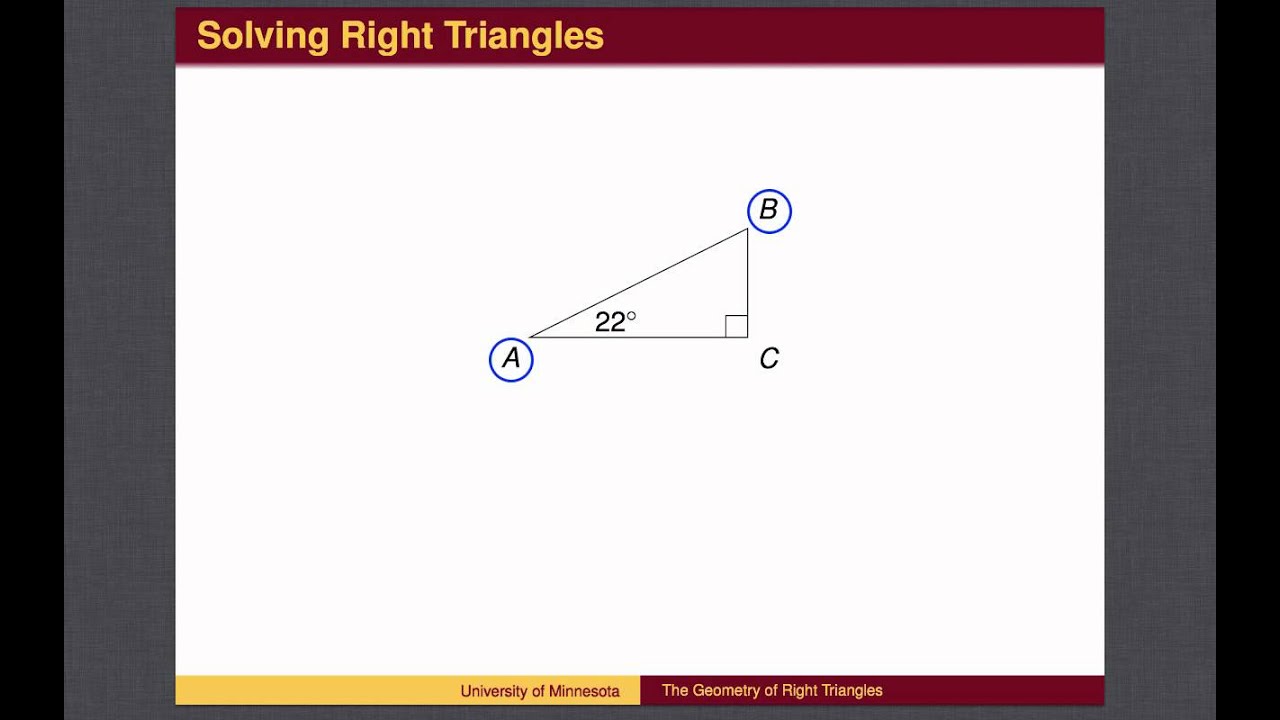
- Let's look at an example. Given , find .
- Solution. Step 1: Determine which trigonometric ratio to use. Let's focus on angle since that is the angle that is explicitly given in the diagram.
- Now let's try some practice problems. Given , find . Round your answer to the nearest hundredth. Given , find . Round your answer to the nearest hundredth.
How do you make a right triangle?
a = √ (c² - b²) if leg b is unknown, then b = √ (c² - a²) for hypotenuse c missing, the formula is c = √ (a² + b²) Given angle and hypotenuse Apply the law of sines or trigonometry to find the right triangle side lengths: a = c * sin (α) or a = c * cos (β) b = c * sin (β) or b = c * cos (α) Given angle and one leg
What does triangle have a right angle?
Other shapes like trapezoids, pentagons, and hexagons can also have a right angle. A triangle with a right angle is a special kind of polygon because it has one right angle and is used in a formula called the Pythagorean theorem. A right triangle has a long side called the hypotenuse.
How to find an angle in a right triangle?
tanθ: It is the ratio of altitude by the base of a right-angled triangle. To find the angles of a right-angled triangle, we can take the trigonometric inverse of the ratio of given sides of the triangle. θ = sin-1x. This returns the angle for which the sine value of the angle is x.

How do you prove that a triangle is a right triangle?
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. That is, in ΔABC, if c2=a2+b2 then ∠C is a right triangle, ΔPQR being the right angle.
What defines right triangle?
A triangle in which one of the interior angles is 90° is called a right triangle. The longest side of the right triangle, which is also the side opposite the right angle, is the hypotenuse and the two arms of the right angle are the height and the base.
Why is the Pythagorean triangle a right angle?
Pythagoras' theorem states that for all right-angled triangles, 'The square on the hypotenuse is equal to the sum of the squares on the other two sides'. The hypotenuse is the longest side and it's always opposite the right angle. In this triangle a 2 = b 2 + c 2 and angle is a right angle.
What kind of triangle is never wrong?
The Right Triangle, Never Wrong.
What's a right angled triangle called?
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle , formerly called a rectangled triangle (Ancient Greek: ὀρθόςγωνία, lit. 'upright angle'), is a triangle in which one angle is a right angle (that is, a 90-degree angle) or two sides are perpendicular.
What are the properties of a right angle triangle?
Properties of Right - Angled Triangle One angle of the triangle always measures 90degree. The hypotenuse is the longest side of the right-angle triangle. The side that is opposite to the 90degree angle is the hypotenuse. The Sum of two interior angles of the right-angled triangle is always 90degree.
Does Pythagoras only work with right triangles?
The Pythagorean Theorem (its converse, really) can be used on any triangle to tell us whether or not it is a right triangle.
What type of triangle can have one right angle?
A scalene triangle is a triangle that has no equal sides or angles. A right triangle is a triangle that has one right (90°) angle. A triangle can be scalene and right if one of its unique angle measures is 90°.
What are the 3 sides of a right triangle?
In a right triangle, the hypotenuse is the longest side, an "opposite" side is the one across from a given angle, and an "adjacent" side is next to a given angle. We use special words to describe the sides of right triangles.
What are two examples of a right triangle?
Special Right Triangles Fully Explained w/ 19 Examples!45-45-90 Triangle.30-60-90 Triangle.
Do all triangles add up to 180?
The angle sum of a triangle will always be equal to 180°. The angle sum of a quadrilateral is equal to 360°, and a triangle can be created by slicing a quadrilateral in half from corner to corner. Since a triangle is essentially half of a quadrilateral, its angle measures should be half as well. Half of 360° is 180°.
How can you quickly identify the long side of a right triangle?
In a right triangle, the side that is opposite of the 90° angle is the longest side of the triangle, and is called the hypotenuse.
Can a right triangle have two equal sides?
A right triangle can also be an isosceles triangle which means that it has two sides and two angles equal. A right isosceles triangle has a 90° ang...
Can 8 cm, 15 cm, and 17 cm form three sides of a right triangle?
We can check if 8 cm, 15 cm, and 17 cm form three sides of a right triangle using the pythagorean theorem. H (Hypotenuse)2 = P (Perpendicular heigh...
What are the 3 sides of the right triangle called?
The base, perpendicular height, and hypotenuse are the three sides of a right triangle.
What is the pythagorean formula for a right-angled triangle?
The Pythagoras theorem states the following formula for a right triangle:H (Hypotenuse)2 = P (Perpendicular height)2 + B (Base)2
What is a right triangle?
What is Right Triangle? A triangle in which one of the interior angles is 90° is called a right triangle. The longest side of the right triangle, which is also the side opposite the right angle, is the hypotenuse and the two arms of the right angle are the height and the base. Here’s what a right triangle looks like:
What are the different types of right triangles?
Types of right triangles. Broadly, right triangles can be categorized as: 1. Isosceles right triangle : In this triangle, one interior angle measures 90° , and the other two angles measure 45° each. It is also known as a 45-90-45 triangle. This is an isosceles right triangle, with ∠A and ∠C measuring 45° each, and ∠B measuring 90° .
What is the measure of a scalene triangle?
In the scalene right triangle ABC, ∠A measures 30°, ∠B measures 90° and ∠C measures 60°. In this triangle, all the three sides will be of different lengths, and the three angles will be of different measures.
Why are the sides AB and AC equal?
Here, the sides AB and AC are equal because of the property that states that sides opposite to equal angles are also equal. 2. Scalene right triangle : This triangle is the one in which one interior angle measures 90°, while the other two measure 30° and 60°.
What is a right triangle?
Right Triangle Definition. All triangles have interior angles adding to 180° 180 °. When one of those interior angles measures 90° 90 ° , it is a right angle and the triangle is a right triangle. In drawing right triangles, the interior 90° 90 ° angle is indicated with a little square □ in the vertex. The term "right" triangle may mislead you ...
How many angles does a right triangle have?
A right triangle must have one interior angle of exactly 90° 90 °. It can be scalene or isosceles but never equilateral.
What is the right triangle altitude theorem?
The right triangle altitude theorem tells us that the altitude of a right triangle drawn to the hypotenuse c c forms two similar right triangles that are also similar to the original right triangle.
What is the Pythagorean theorem?
You also know what the Pythagorean Theorem is ( a2 + b2 = c2 a 2 + b 2 = c 2) and how to prove it, and what the right triangle altitude theorem is (the altitude of a right triangle drawn to the hypotenuse c c forms two similar right triangles that are also similar to the original right triangle) and how to prove it.
How to tell if a new triangle is similar to the original triangle?
You can prove this by seeing that new triangle's ∠ADC ∠ A D C = original triangle's ∠AC B ∠ A C B, while new triangle's ∠C AD ∠ C A D = original triangle's ∠C AB ∠ C A B.
Is the vertex of a right triangle a right angle?
We already know the square vertex of the right triangle is a right angle. Opposite it is the triangle's hypotenuse, the longest of the three sides, usually labeled c c.
What is the right triangle?
A Right triangle has a right angle for one of its corners. The presence of this right angle makes a lot of the maths for calculating the other lengths and angles much simpler, and hence why it is useful to have a classification for this kind of triangle.
Why is a right triangle called a right triangle?
Right triangle is called because of the presence of a right angle but we don't have any left angle so we don't use it as left triangle..
How many angles does a triangle have?
A triangle has 3 angles in it nd d sum of all equals 180*. Whenever any one of the angles is 90* then the triangle is called a right angled triangle .
What is the right appellation?
The 'right' appelation pertains to there being a 90 degree angle in the right triangle which is being highlighted as the triangles' special or distinguishing feature. This then begs the question:
Why is it called a right angle?
A right angle is called such because it borrows from the Latin: angulus rectus, or "upright angle" (because if you have a line that's 90 degrees from the ground, it would be upright). You don't have a "left angle" because in this context, you're not using the "right-left" definition of the word "right", and so it doesn't logically follow from the existence of the "right angle", that there should be a "left angle".
How to find the third side of a right angle triangle?
If u know two sides of a right angle triangle then we can find third side using pythagores theorem
How many radians are in a right triangle?
Right triangle: One angle = 90° or π/2 radi ans.
What is a right triangle (or right-angled triangle)?
The definition is very simple and might even seem obvious for those who already know it: a right-angled triangle is a triangle where one and only one of the angles is exactly 90°. The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°.
How to find the area of a right triangle?
All that you need are the lengths of the base and the height. In a right triangle, the base and the height are the two sides which form the right angle.
How to find the base of a triangle if you don't know the height?
If you don't know the base or the height, you can find it using the Pythagorean theorem. Use the right triangle calculator to check your calculations or calculate the area of triangles with sides that have larger or decimal value length.
How to solve for hypotenuse in a right triangle?
To solve for c, take the square root of both sides to get c = √ (b²+a²).
What happens if you separate rectangles by diagonals?
If we separate the rectangle by the diagonal, what will we obtain is two right-angled triangles. Looking at the triangles, there is no need to use the right triangle calculator to see that both are equal, so their areas will be the same. This means that the area of the rectangle is double that of each triangle.
Which triangle has 2 sides of equal length?
Another of special triangles is the isosceles triangle, which has 2 sides of equal length, and hence two angles of the same size. As opposed to the equilateral triangle, isosceles triangles come in many different shapes, but all have certain properties that are exploited by the isosceles triangle calculator to obtain all the parameters of these triangles.
What are the sets of numbers that satisfy the Pythagorean theorem?
These sets of numbers are called the Pythagorean triplets and are sets of 3 integers (let's call the a, b and c) and satisfy the Pythagorean theorem: a² + b² = c². That is, they could form a right triangle with sides of length a, b and c. The amount of numbers that satisfy this relationship is limited but mathematicians find joy in searching for new ones.
Why are right triangles useful?
Right triangles are very useful in our daily life. The simpler the dimensions of a right triangle, the simpler is its use. The ability to recognize special right triangles is the shortcut to solving problems involving right triangles. Instead of using the Pythagorean theorem, you can use special right triangle ratios to calculate ...
What is a 3-4-5 Right Triangle?
A 3-4-5 right triangle is a triangle whose side lengths are in the ratio of 3:4:5. In other words, a 3-4-5 triangle has the ratio of the sides in whole numbers called Pythagorean Triples.
How many angles are there in a triangle?
A triangle is a two-dimensional polygon with three corners, three vertices, and three angles joined together, forming a closed diagram in geometry. There are different types of triangles depending on the side lengths and magnitude of their interior angles.
What is the internal angle of a 3 4 5 right triangle?
A 3-4-5 right triangle has the three internal angles as 36.87 °, 53.13 °, and 90 °. Therefore, a 3 4 5 right triangle can be classified as a scalene triangle because all its three sides lengths and internal angles are different.
How long is a diagonal?
Therefore, the length of the diagonal is 10 inches.