In fact, regardless of the value of θ, the Pythagorean identity will remain true for all angle measures. This is what makes these identities helpful – we can simplify complex trigonometric expressions and use them to rewrite and prove identities.
How to solve Pythagorean identities?
- Start with this first Pythagorean Identity.
- Divide each term by sin2θ.
- We know and .
- Substitute and simplify.
How to do the pyhagorean identiy?
Solutions
- First we can factor a 4 out of the second two terms. Then we can use the first Pythagorean identity to simplify to get:
- First, distribute the 7cot ( x ), then combine like terms, and factor out a 7 to be able to use the second Pythagorean identity.
- First, distribute the -3 and then rearrange to apply the third Pythagorean identity.
What does the Pythagorean theorem allow us to do?
The Pythagorean theorem is useful for architects as it plays a role in determining the size and shape of structures. With the help of this theorem, they can check building proportions. An architect deals with the design of a building, and this building has to be functional, safe, and at the same time aesthetically pleasing for the environment.
What does the Pythagorean theory explain?
Pythagorean Theorem: Definition & Example
- Right Triangles. The three letters used in the equation form of the Pythagorean Theorem are specific to right triangles only.
- The Sides. Once you have your right triangle, you can label its sides appropriately with the letters. ...
- Application. So, why is the Pythagorean Theorem such a big deal? It is a big deal because it is so useful. ...
How do you prove the Pythagorean identity?
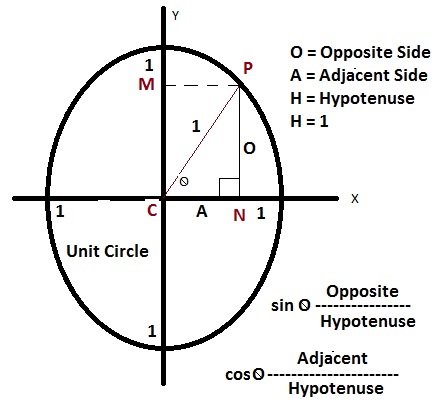
The Pythagorean identity tells us that no matter what the value of θ is, sin²θ+cos²θ is equal to 1. We can prove this identity using the Pythagorean theorem in the unit circle with x²+y²=1.
Why are Trig identities true?
Trigonometric Identities are true for every value of variables occurring on both sides of an equation. Geometrically, these identities involve certain trigonometric functions (such as sine, cosine, tangent) of one or more angles.
Why do we use the Pythagorean identity?
Pythagorean identities are useful in simplifying trigonometric expressions, especially in writing expressions as a function of either sin or cos, as in statements of the double angle formulas.
Where does the Pythagorean identity come from?
Pythagorean identities are formulas, derived from Pythagorean Theorem, that allow us to find out where a point is on the unit circle.
How do you prove something is an identity?
To prove an identity is to show that the expressions on each side of the equation are the same for every allowable input.
How will you verify if an equation is identity?
If solving a linear equation leads to a true statement such as 0 = 0, the equation is an identity.
Why does the Pythagorean theorem work?
0:132:37Pythagorean Theorem explained - YouTubeYouTubeStart of suggested clipEnd of suggested clipRemember the area of a square is side squared. So from this we get a squared plus b squared is equalMoreRemember the area of a square is side squared. So from this we get a squared plus b squared is equal to C squared. And by rearranging the shapes we can see that this is true.
Can Pythagorean identities be negative?
the Pythagorean identity. In the figure, the point P has a negative x-coordinate, and is appropriately given by x = cosθ, which is a negative number: cosθ = −cos(π−θ ). Point P has a positive y-coordinate, and sinθ = sin(π−θ ) > 0.
What are the 3 Pythagorean identities?
0:017:42Pythagorean Identities - Examples & Practice Problems, TrigonometryYouTubeStart of suggested clipEnd of suggested clipNow let's talk about the pythagorean identities there's three of them that you need to be aware ofMoreNow let's talk about the pythagorean identities there's three of them that you need to be aware of the first one is the most common sine squared of theta plus cosine squared theta is equal to one
How do you simplify Pythagorean identities?
2:5912:47How to Simplify Pythagorean Identities | 18 Examples - YouTubeYouTubeStart of suggested clipEnd of suggested clipYou know we know sine over cosine is tangent so sine squared over cosine squared is going to beMoreYou know we know sine over cosine is tangent so sine squared over cosine squared is going to be tangent squared of theta. And one over cosine is secant.
Are all trig identities true?
In math, an "identity" is an equation that is always true, every single time. Trig identities are trigonometry equations that are always true, and they're often used to solve trigonometry and geometry problems and understand various mathematical properties.
How do you prove trigonometric identities easily?
17:3625:08Verifying Trigonometric Identities Easily - Strategy Explained (14 ...YouTubeStart of suggested clipEnd of suggested clip1 minus cosine squared equals sine squared. And we proved it ok number 11 how would you do this oneMore1 minus cosine squared equals sine squared. And we proved it ok number 11 how would you do this one sine theta times tangent theta all over 1 minus cosine theta. Minus 1 equals secant theta.
How do you prove trigonometric ratios?
The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and secant (sec)....Trigonometric RatiosSin θOpposite Side to θ/HypotenuseCos θAdjacent Side to θ/HypotenuseTan θOpposite Side/Adjacent Side & Sin θ/Cos θCot θAdjacent Side/Opposite Side & 1/tan θ2 more rows•Jan 31, 2020
What are the fundamental trigonometric identities?
To sum up, only two of the trigonometric functions, cosine and secant, are even....Verifying the Fundamental Trigonometric Identities.Quotient Identitiestan θ = sin θ cos θ tan θ = sin θ cos θcot θ = cos θ sin θ cot θ = cos θ sin θDec 21, 2021
What are Pythagorean Identities?
Pythagorean identities are important identities in trigonometry that are derived from the Pythagoras theorem. These identities are used in solving many trigonometric problems where one trigonometric ratio is given and the other ratios are to be found.
Pythagorean Identities Derivation
We are going to prove the Pythagorean identities using the Pythagoras theorem. Let us consider a right-triangle ABC that is right-angled at C. Then AB is the hypotenuse. Let us assume that AB = c, BC = a, and CA = b for our convenience. Let us assume that the angle at B is θ.
Pythagorean Identities Examples
Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.
Faqs on Pythagorean Identities
Here are the 3 Pythagorean identities. Each identity can be written in alternative ways as shown.
What does the teacher explain about squares protruding from the sides of a triangle?
They do the obvious thing: squares protruding from the triangle’s sides, and explain that the surface areas of the smaller ones taken together match the surface area of the big one.
What do you remember from geometry class?
If you’ve ever taken a geometry class, the one thing you’re likely to still remember from it is the relationship among the sides of a right triangle.
What do we know?
If we want to convince ourselves that the theorem is true. What do we accept as given?
What is the area of a right triangle?
Duplicating and flipping a right triangle gives us a rectangle shape. Since the rectangle is constructed from two identical halves, we know the area of the right triangle to be (a × b) / 2
Can you animate a triangle with different sides?
Even if you animate it with changing sides of the triangle, you never get any kind of congruence that would be convincing visually. The proportions might seem about right, but exact equality still seems like a leap of faith.
What are the Pythagorean identities?
Pythagorean Identities Definition. The Pythagorean identities in trigonometry are the three identities that come from the Pythagorean theorem. Recall that the Pythagorean theorem states that the hypotenuse squared of a right triangle is the sum of the square of each of the other two sides, or a squared plus b squared equals c squared, ...
How to find the third identity of a trigonometric equation?
To do this, we need to divide our first identity by cosine squared. We already know some trigonometry properties, such as sine squared divided by cosine squared equals tangent squared, and that 1 divided by cosine squared is secant squared. Having all this information allows us to arrive at our third identity: tangent squared plus 1 equals secant squared.
How to find the second identity of a cosine squared?
To arrive at this identity, we divided our first identity by sine squared so as to get the one side to equal 1. We know that cosine squared divided by sine squared is cotangent squared, and we also know that 1 divided by sine squared is cosecant squared. Using these properties, we arrive at our second identity: 1 plus cotangent squared is cosecant squared.
What does C stand for in the Pythagorean theorem?
In the Pythagorean theorem, c stands for the hypotenuse, and a and b stand for the other two sides of the right triangle. From this theorem, three identities can be determined from substituting in sine and cosine.
What is the hypotenuse of a triangle?
All the right triangles formed by the unit circle will have a hypotenuse of 1. With a hypotenuse of 1 and with our angle at the origin of the coordinate plane on which the unit circle is drawn, we can determine some relationships between the sides and our sine and cosine. The unit circle triangle with a hypotenuse of 1.
Do you have to be a Study.com member to unlock this lesson?
To unlock this lesson you must be a Study.com Member.
Is sin positive in the first quadrant?
4. First note that since x is in the first quadrant, sin ( x) will be positive. Now, using the third Pythagorean identity, we know that:
What is Pythagorean identity?
Pythagorean identities. Pythagorean identities are formulas, derived from Pythagorean Theorem, that allow us to find out where a point is on the unit circle. Learn the tricks and tips on how to use the unit circle to derive and prove the Pythagorean identities can be difficult. Basic Concepts.
What is the first state of the Pythagorean identities?
Let's explore the Pythagorean identities. The first of these three states that sine squared plus cosine squared equals one. The second one states that tangent squared plus one equals secant squared. For the last one, it states that one plus cotangent squared equals cosecant squared.
What is the Pythagoras theorem?
What is the Pythagoras theorem? The Pythagoras tells us that X squared plus Y squared equals to the hypotenuse squared. The hypotenuse in this case is one, since we're using a unit circle. So here we have X squared plus Y squared equals one squared.
What is the difference between X and Y coordinates?
The X coordinate can be represented as cosine theta, while its Y coordinate can be represented as sine theta. Keep in mind that this is only for a unit circle. So for any point on the unit circle: the X coordinate can be represented as cosine theta; the Y coordinate can be represented as sine theta.
How many practice questions are there in trigonometry?
We have over 250 practice questions in Trigonometry for you to master.
Is one squared a cosine theta?
Through using the unit circle, the answer becomes very obvious. One squared is just one. The X coordinate can also be represented as cosine theta. The Y coordinate can be represented as sine theta. And voila! We are done. From the unit circle, we've successfully proved that cosine squared plus sine squared equals one, tackling one out of 3 Pythagorean identities.

Pythagorean Trig Identities
- All Pythagorean trig identities are mentioned below together. Each of them can be written in different forms by algebraic operations. i.e., each Pythagorean identity can be written in 3 forms as follows: 1. sin2θ + cos2θ = 1 ⇒ 1 - sin2θ = cos2 θ ⇒ 1 - cos2θ = sin2θ 2. sec2θ - tan2θ = 1 ⇒ sec2θ = 1 + tan2θ ⇒ sec2θ - 1 = tan2θ 3. csc2θ - cot2θ = 1 ⇒ ...
Proof of Pythagorean Identity sin²θ + Cos²θ = 1
- Applying the Pythagoras theorem to the triangle, we get a2 + b2 = c2 Dividing each term on both sides by c2, a2 / c2 + b2 / c2 = c2 / c2 (a / c)2 + (b / c)2= 1 (cos θ)2 + (sin θ)2= 1 (or) sin2θ + cos2θ = 1 Hence proved.
Proof of Pythagorean Identity Sec²θ - Tan²θ = 1
- Again, by Pythagoras theorem a2 + b2 = c2 Dividing each term on both sides by a2, a2 / a2 + b2 / a2 = c2 / a2 1 + (b / a)2 = (c / a)2 1 + (tan θ)2 = (sec θ)2 (or) sec2θ - tan2θ = 1 Hence proved.
Proof of Pythagorean Identity Csc²θ - Cot²θ = 1
- By Pythagoras theorem, a2 + b2 = c2 Dividing each term on both sides by b2, a2 / b2 + b2 / b2 = c2 / b2 (a / b)2 + 1 = (c / b)2 (cot θ)2 + 1 = (csc θ)2 (or) csc2θ - cot2θ = 1 Hence proved. 1. Pythagorean identities are used to prove other trigonometric identies. Example: Prove the identity sin4x - cos4x = sin2x - cos2x. Solution: We can write LHS = sin4x - cos4x = (sin2x)2 - (cos2x)2 …