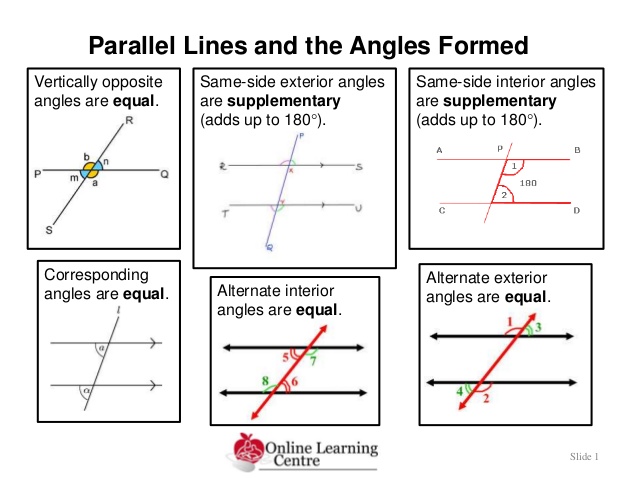
NARUTO77SAMA When all of the angles of a convex polygon converge, or pushed together, they form one angle called a perigon angle, which measures 360 degrees. If the sides of the convex polygon are increased or decreased, the sum of all of the exterior angle is still 360 degrees.
What is the sum of all exterior angles of a triangle?
Therefore the Sum of exterior angles = 360° Thus, the sum of all exterior angles of a triangle is 360°. In the same way, we can prove that the sum of all exterior angles of any polygon is 360°. Thus, the sum of exterior angles can be obtained from the following formula:
Is the sum of the exterior angles of a polygon 360 degrees?
It is not true that the sum of the exterior angles of any polygon is 360 degrees, unless there is some specification of the signs of the angles based on some convention about the relation of one vertex to another. I exhibit one that does not have the 360 property.
What is the sum of the exterior angles of a vertex?
Each rotation angle is the exterior angle. Since you come back to the original vertex, you have added all exterior angles and that sum is 360 degrees. (To be back is to have gone full circle, and that is 360 degrees). Easily convert PDF to any format with pdfFiller PDF converter.
How to find the sum of interior angles of a polygon?
By the sum of interior angles formula, Sum of interior angles of any polygon = 180 (n - 2)° By adding the above two equations, we get the sum of all n interior angles and the sum of all n exterior angles: 360° + 180 (n - 2)° = 360° + 180n - 360° = 180n

Why is the sum of the exterior angles of a triangle 360?
0:274:57Prove That the Sum of Exterior Angles in a Triangle is 360 DegreesYouTubeStart of suggested clipEnd of suggested clipThat X plus y plus Z is equal to 360 degrees. Now since we have a triangle ABC. We know angle A plusMoreThat X plus y plus Z is equal to 360 degrees. Now since we have a triangle ABC. We know angle A plus angle B plus angle C is equal to 180 degrees that is sum of interior. Angles.
Is the sum of exterior angles always 360?
The sum of exterior angles in a polygon is always equal to 360 degrees. Therefore, for all equiangular polygons, the measure of one exterior angle is equal to 360 divided by the number of sides in the polygon. an exterior angle.
How do you prove that the sum of the exterior angles of a polygon is 360 degrees?
So, the sum of exterior angles is a + b + c + d + e = 5(180) – sum of interior angles. So, we do from (1) a + b + c + d + e = 5(180) – 540 = 900 – 540 = 360 degrees. Therefore sum of exterior angles in any of the polygon is 360 degrees.
Is sum of three exterior angles always 360?
Sum of Exterior Angles of a Triangle Formula We know that the sum of all the exterior angles of any polygon is equal to 360°.
How do you prove the sum of the exterior angles?
1:022:33Prove: Sum of Exterior Angles of Any Polygon is 360 - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo this sum sum of our exterior angle sum sum of exterior. Ones is going to be sum of the semicircleMoreSo this sum sum of our exterior angle sum sum of exterior. Ones is going to be sum of the semicircle sum of 180 degrees.
How do you prove the exterior angle theorem?
Hence proved that the exterior angle of a triangle is equal to the sum of the two opposite interior angles....Proof of Exterior Angle Theorem.StatementReason∠a + ∠b = ∠x + ∠yFrom the above statements∠ACD = ∠x + ∠yFrom the construction of CE∠a + ∠b = ∠ACDFrom the above statements2 more rows
Do exterior angles add up to 180?
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
Is a triangle 360 or 180?
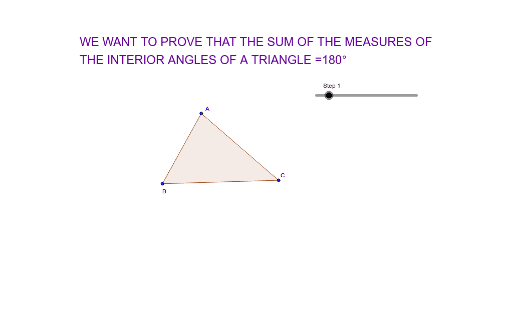
The angle sum of a triangle will always be equal to 180°. The angle sum of a quadrilateral is equal to 360°, and a triangle can be created by slicing a quadrilateral in half from corner to corner. Since a triangle is essentially half of a quadrilateral, its angle measures should be half as well. Half of 360° is 180°.
What is the sum of all exterior angles of a polygon?
The sum of all the exterior angles in a polygon is equal to 360 degrees.
Are all triangles 360 degrees?
Why Does a Triangle Have 180 Degrees? A triangle's angles add up to 180 degrees because one exterior angle is equal to the sum of the other two angles in the triangle.
What is the sum of all exterior angles of a pentagon?
Sum of Exterior Angles in a Pentagon We know that each exterior angle is supplementary to the interior angle. Therefore, the sum of exterior angles of a polygon = n(360°/n). As, the number of sides in a pentagon is 5, n=5. Thus, the sum of exterior angles of a pentagon = 5(360°/5) = 360°.
Do exterior angles add up to 180?
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
Is a triangle 360 or 180?
The angle sum of a triangle will always be equal to 180°. The angle sum of a quadrilateral is equal to 360°, and a triangle can be created by slicing a quadrilateral in half from corner to corner. Since a triangle is essentially half of a quadrilateral, its angle measures should be half as well. Half of 360° is 180°.
Do interior angles add up to 360?
So, the sum of the interior angles of a quadrilateral is 360 degrees. All sides are the same length (congruent) and all interior angles are the same size (congruent).
Method 1
We're going to move copies of our septagon so that the highlighted angles "stack" on top of each other: so that their vertices match up. Let's stack them at the corner which houses our p u r p l e \textcolor {purple} {\text {purple}} purple angle.
Method 2
This is one way to "see" it inside your head. Another way to prove that the sum of the exterior angles of a polygon is 3 6 0 ∘ 360^ {\circ} 360∘ is to use a different method: to chop up the septagon into triangles.
Method 3: The "Bus" Proof
Pretend the perimeter of the polygon is a road, and you're on a bus driving along it. At every vertex, the angle of your direction changes. You drive a loop around the shape and return to the same spot that you started at. So you "turned" by one full revolution, which is 3 6 0 ∘! 360^ {\circ}! 360∘!
What is the sum of exterior angles?
This can be understood clearly by observing the exteriors angles in the below triangle. The sum of exterior angles formula says the sum of all exterior angles in any polygon is 360°.
How many degrees are there in a hexagon?
Answer: Each exterior angle of a regular hexagon = 60°. Example 2: Use the sum of exterior angles formula to prove that each interior angle and its corresponding exterior angle in any polygon are supplementary.