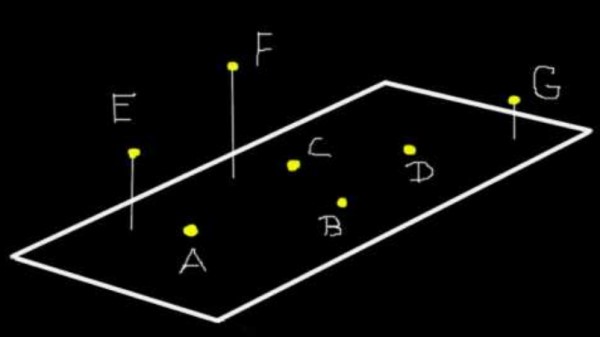
¿Cuáles son los vectores coplanares y no coplanares?
Un sistema de vectores coplanares es aquel en el cual los vectores se encuentran en el mismo plano, o sea, en dos ejes; si están en diferente plano, o en tres ejes, son no coplanares Page 17 Page 18 Un sistema de vectores colineales se presenta cuando los vectores se localizan en una sola dirección o línea de acción.
¿Cuáles son los puntos coplanares?
En geometría, un conjunto de puntos en el espacio es coplanario (el anglicismo coplanar es incorrecto) si todos los puntos se encuentran en el mismo plano.
¿Qué es no coplanares en la recta?
Definiciones: Dos o más puntos que pertenecen a un mismo plano se denominan puntos coplanares. En caso contrario, se dicen no coplanares. Dos o más rectas contenidas en un mismo plano se denominan rectas coplanares • Dos rectas que se intersecan en un punto se dice que se cortan en un punto.
¿Qué es colineales y no colineales?
Cuando dos segmentos comparten un punto extremo, son segmentos consecutivos. Entre ellos, los segmentos colineales son los que se ubican en una misma recta. Por el contrario, cuando los segmentos consecutivos se desarrollan en rectas diferentes se habla de segmentos no colineales.
¿Qué significa que son coplanarias?
Dicho de dos o más líneas o figuras : Que están en un mismo plano .5 days ago
¿Cuáles son los puntos colineales y coplanares?
Diremos que dos o más puntos son alineados (o colineales) si pertenecen a una misma recta. d es exterior a la recta R. Diremos que dos o más puntos son coplanares si pertenecen a un mismo plano.
¿Cómo saber si son coplanares?
Dos o más vectores son coplanarios si son linealmente dependientes, y por tanto sus componentes son proporcionales y su rango es 2. Para que el rango sea igual a 2, el determinante de las componentes de los vectores ha de ser igual a cero.
¿Qué son rectas coplanares y Alabeadas?
RECTAS QUE SE CRUZAN (ALABEADAS) Son rectas que no se cortan y no son paralelas, por lo tanto no son coplanares.
¿Que determinan tres puntos que no son colineales?
Propiedad 5: tres puntos no colineales determinan un único plano. Dos puntos determinan una recta y por una recta pasan infinitos planos; sin embargo, cuando se tienen tres puntos, solo existe un único plano que los contiene.
¿Qué son puntos no colineales y ejemplos?
Los puntos D , B , y E caen en la línea n . Ellos son colineales. No hay una línea que pase a través de los tres puntos A , B , y D . Así, estos no son colineales.
¿Qué significa que sean colineales?
En cualquier geometría, un conjunto de puntos situados sobre una misma línea se dice que es colineal. En geometría euclidiana, esta relación se visualiza intuitivamente mediante puntos que se encuentran situados sobre una "línea recta".
¿Cuáles son las fuerzas no colineales?
Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben aplicarse métodos analíticos o geométricos.
Ecuación de un plano dado tres puntos
La ecuación de un plano determinado por tres puntos conocidos A, B, C es una relación matemática que garantiza que cualquier punto P de coordenadas genéricas (x, y, z) que cumpla la ecuación pertenece a dicho plano.
Ejercicios resueltos
Un plano intersecta a los ejes cartesianos X, Y, Z en 1, 2 y 3 respectivamente. La intersección de dicho plano con los ejes determina los puntos A, B y C. Encontrar la componente Dz de un punto D, cuyas componentes cartesianas son:

Vectores Coplanares Y Ecuación Del Plano
Condiciones para Que Tres Vectores Sean No Coplanares
- Como se ha visto en la sección previa la condición AQ• (u Xv) = 0 garantiza que el vector AQ es coplanario a u y v. Si denominamos w al vector AQentonces podemos afirmar que: w, u y v son coplanares, si y sólo si w • (u X v) = 0.
Ejercicios Resueltos
- -Ejercicio 1
Se tienen tres vectores u = ( -3, -6, 2); v = (4, 1, 0) y w= (-1, 2, z) Note que la componente z del vector wes desconocida. Encuentre el intervalo de valores que puede tomar z de modo tal que se garantice que los tres vectores no comparten el mismo plano. - -Ejercicio 2
Encuentre el volumen del paralelepípedo mostrado en la siguiente figura:
Referencias
- Figueroa, D. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. 31-68.
- Física. Módulo 8: Vectores. Recobrado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecánica para Ingenieros. Estática. 6ta Edición. Compañía Editorial Continental.28-66.
- McLean, W. Serie Schaum. Mecánica para Ingenieros: Estática y Dinámica. 3ra Edición. McGr…
- Figueroa, D. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. 31-68.
- Física. Módulo 8: Vectores. Recobrado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecánica para Ingenieros. Estática. 6ta Edición. Compañía Editorial Continental.28-66.
- McLean, W. Serie Schaum. Mecánica para Ingenieros: Estática y Dinámica. 3ra Edición. McGraw Hill. 1-15.