First of all, level curves are determined by the relationship between an animal’s level (coordinates) and its respective ground level. Second, the curve is typically shaped in a way that makes the animal’s level curve more or less parallel to the ground.
How to find the level curve of a graph?
What is a level curve?
What is the equation of an ellipse centered at (x 0, y 0)?
What is the equation of a circle of radius R centered at?
What is the term for the level surfaces of a 3-space?
Can level curves extend to functions of three or more variables?
See 1 more
How do you find a level curve?
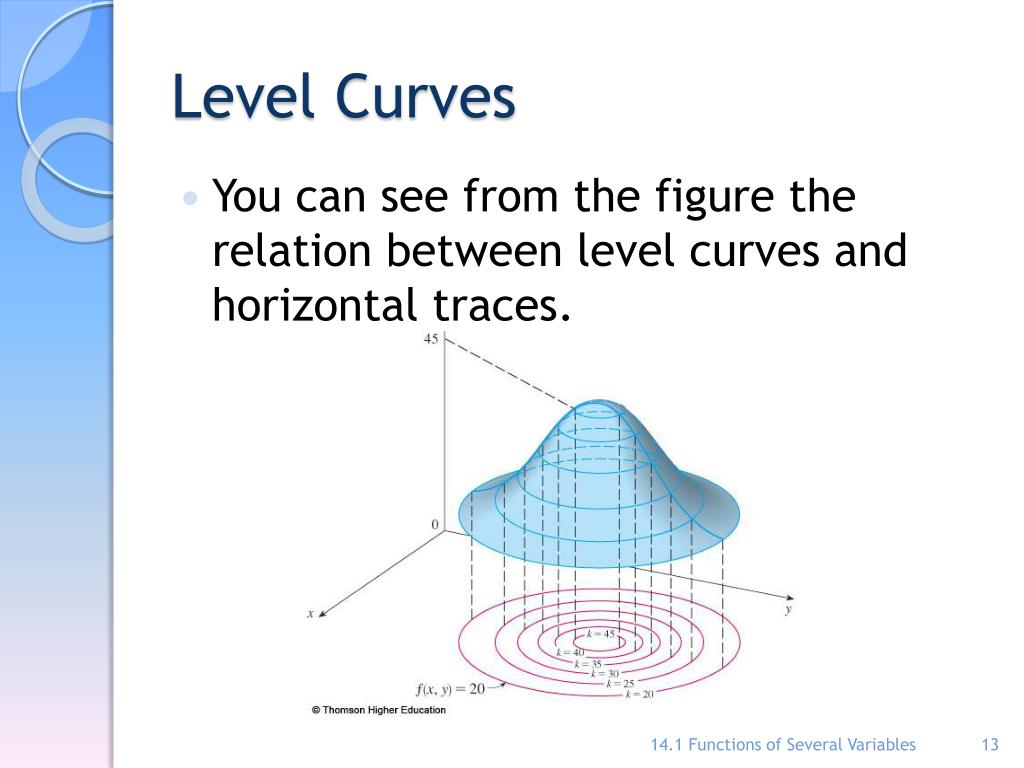
A level curve of a function f(x,y) is the curve of points (x,y) where f(x,y) is some constant value. A level curve is simply a cross section of the graph of z=f(x,y) taken at a constant value, say z=c. A function has many level curves, as one obtains a different level curve for each value of c in the range of f(x,y).
What does a level curve tell you?
A level curve of the surface is a two-dimensional curve with the equation , where k is a constant in the range of f. A level curve can be described as the intersection of the horizontal plane with the surface defined by f. Level curves are also known as contour lines.
How do you match a level curve equation?
1:338:17Matching Functions to Level Curves - YouTubeYouTubeStart of suggested clipEnd of suggested clipWe can do all this algebraically. So starting with the equation z equals x squared plus y squaredMoreWe can do all this algebraically. So starting with the equation z equals x squared plus y squared and setting z equal to k. We get the equation x squared plus y squared equals k.
How do you know if level curves cross at right angles?
At points (x, y) where the gradients are defined and are not the zero vector, the level curves of f and g intersect at right angles if and only Vf · Vg = 0. We have Vf · Vg = (5i + 5j) · (5i − 5j)=0 , which is zero at all points, so the level curves of f intersect those of g in right angles.
What is an example of level curve?
0:0010:16Level Curves of Functions of Two Variables - YouTubeYouTubeStart of suggested clipEnd of suggested clipWelcome to a video on level curves the goals of this video are to graph the level curves of a givenMoreWelcome to a video on level curves the goals of this video are to graph the level curves of a given function as well as recognize a function graphed using level curves level curves sometimes called
Why are level curves useful?
Level curves can show you areas where temperature, stress, or concentrations are within some interval. Finally, level curves are useful if your function is sufficiently complicated that it is difficult to visualize a 3-D rendering of the surface that it makes.
How do you find the slope of a level curve?
1:377:49Slope of a level curve - YouTubeYouTubeStart of suggested clipEnd of suggested clipThe solution to this problem is that Y prime the slope of the level curve is equal to minus theMoreThe solution to this problem is that Y prime the slope of the level curve is equal to minus the partial derivative of F with respect.
How do you match a function with level curves?
0:027:31matching level curves with functions - YouTubeYouTubeStart of suggested clipEnd of suggested clipYou have these four functions. And you are to match with the level curves over here. And you have toMoreYou have these four functions. And you are to match with the level curves over here. And you have to know that lighter color means higher elevation.
What is difference between a curve and a level curve?
Curves provides more customized contrast control than Levels. Levels provides enhancement of contrast only by setting highlight and shadow points. Curves allows you to adjust contrast by setting and positioning control points along the entire tonal range.
How do you know which curve is above the other?
All you need to do is pick a point on each interval (between the intersection points and/or the given endpoints of the interval), and evaluate both curves at that point. Whichever curve returns the larger value is the curve on the top.
How do you know if two lines make a right angle?
Perpendicular is a term that describes the relationship between two lines. You can determine if two lines intersect at a right angle by checking if they intersect at 90°.
Are contour lines and level curves the same?
A contour line (also known as a level curve) for a given surface is the curve of intersection of the surface with a horizontal plane, z = c. A representative collection of contour lines, projected onto the xy-plane, is a contour map or contour plot of the surface.
What are level curves in complex analysis?
A level curve is a continuous, analytic function that intersects the level lines in a given family of level planes in complex analysis. A family of level planes can either be a two-dimensional or three-dimensional family. Level curves are often used in complex analysis.
What does it mean for a level curve to be empty?
The level set of f is empty if there is no point (x,y) in the domain of f for which f(x,y) = c.
What is difference between a curve and a level curve?
Curves provides more customized contrast control than Levels. Levels provides enhancement of contrast only by setting highlight and shadow points. Curves allows you to adjust contrast by setting and positioning control points along the entire tonal range.
What does level mean on a graph?
In the mathematical subfield of graph theory a level structure of an undirected graph is a partition of the vertices into subsets that have the same distance from a given root vertex.
How to find the level curve of a graph?
The level curves are given by x 2 − y 2 = c . For c = 0, we have x 2 = y 2; that is, y = ± x, two straight lines through the origin. For c = 1, the level curve is x 2 − y 2 = 1, which is a hyperbola passing vertically through the x -axis at the points ( ± 1, 0). For c = 2, the level curve is ( x 2) 2 − ( y 2) 2 = 1, which is a hyperbola passing vertically through the x -axis at the points ( ± 2, 0). For c = − 1, we have y 2 − x 2 = 1, the hyperbola passing horizontally through the y -axis at the points ( 0, ± 1).
What is a level curve?
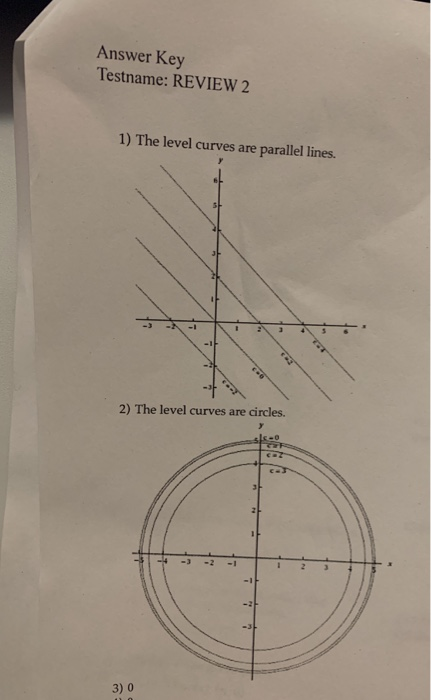
The graph of this function is a plane. The level curves are parallel lines of the form
What is the equation of an ellipse centered at (x 0, y 0)?
Recall that ( x − x 0) 2 a 2 + ( y − y 0) 2 b 2 = 1 is the equation of an ellipse centered at ( x 0, y 0) with semi major axis a and semi minor axis b (if a ≥ b ).
What is the equation of a circle of radius R centered at?
Recall that ( x − x 0) 2 + ( y − y 0) 2 = R 2 is the equation of a circle of radius R centered at ( x 0, y 0)
What is the term for the level surfaces of a 3-space?
If f ( x, y, z) gives the temperature at each point of 3-space, the level surfaces (curves of constant temperature) are called isothermal. In physics, when f ( x, y, z) is a potential function, which gives the value of the potential energy at each point of space, the level surfaces are called equipotential or isopotential. Figure 11 shows the electrostatic equipotentials between two electric charges.
Can level curves extend to functions of three or more variables?
We can extend the concept of level curves to functions of three or more variables.
What is the level curve of a function?
Definition: The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ).
How to visualize a function of two varibles?
One of the most useful and common methods for visualizing functions (or surfaces) of two varibles is a Contour Map in which points of constant elevation are joined in a 2D plane to form level curves (or contour curves ).
How to find the equation of the curve in the xy plane?
Find an equation of the curve in the xy plane which passes through the point (1,1) and intersects all level curves of the function f ( x, y) = x 4 + y 2 at right angles.
Is a level curve orthogonal to a level curve of f?
All level curves of g will be orthogonal to level curves of f; now simply choose the one where g ( 1, 1) = g ( x, y).
How to find the level curve of a function?
The level curves of the function z = f (x,y) z = f ( x, y) are two dimensional curves we get by setting z = k z = k , where k k is any number . So the equations of the level curves are f (x,y) = k f ( x, y) = k. Note that sometimes the equation will be in the form f (x,y,z) = 0 f ( x, y, z) = 0 and in these cases the equations of the level curves are f (x,y,k) = 0 f ( x, y, k) = 0.
How to get an equation for a trace?
We’ll start with x = 1 x = 1. We can get an equation for the trace by plugging x = 1 x = 1 into the equation. Doing this gives,
How to graph a plane?
To graph a plane we will generally find the intersection points with the three axes and then graph the triangle that connects those three points. This triangle will be a portion of the plane and it will give us a fairly decent idea on what the plane itself should look like.
Can you take a logarithm of a negative number?
In this final part we know that we can’t take the logarithm of a negative number or zero. Therefore, we need to require that,
Can you graph contour curves?
Of course, we probably don’t have the function that gives the elevation, but we can at least graph the contour curves.
How to find the level curve of a graph?
The level curves are given by x 2 − y 2 = c . For c = 0, we have x 2 = y 2; that is, y = ± x, two straight lines through the origin. For c = 1, the level curve is x 2 − y 2 = 1, which is a hyperbola passing vertically through the x -axis at the points ( ± 1, 0). For c = 2, the level curve is ( x 2) 2 − ( y 2) 2 = 1, which is a hyperbola passing vertically through the x -axis at the points ( ± 2, 0). For c = − 1, we have y 2 − x 2 = 1, the hyperbola passing horizontally through the y -axis at the points ( 0, ± 1).
What is a level curve?
The graph of this function is a plane. The level curves are parallel lines of the form
What is the equation of an ellipse centered at (x 0, y 0)?
Recall that ( x − x 0) 2 a 2 + ( y − y 0) 2 b 2 = 1 is the equation of an ellipse centered at ( x 0, y 0) with semi major axis a and semi minor axis b (if a ≥ b ).
What is the equation of a circle of radius R centered at?
Recall that ( x − x 0) 2 + ( y − y 0) 2 = R 2 is the equation of a circle of radius R centered at ( x 0, y 0)
What is the term for the level surfaces of a 3-space?
If f ( x, y, z) gives the temperature at each point of 3-space, the level surfaces (curves of constant temperature) are called isothermal. In physics, when f ( x, y, z) is a potential function, which gives the value of the potential energy at each point of space, the level surfaces are called equipotential or isopotential. Figure 11 shows the electrostatic equipotentials between two electric charges.
Can level curves extend to functions of three or more variables?
We can extend the concept of level curves to functions of three or more variables.
