Skew Lines in a Cube
- Find lines that do not intersect each other.
- Check if these pairs of lines are also not parallel to each other.
- Next, check if these non-intersecting and non-parallel lines are non-coplanar. If yes then the chosen pair of lines are skew lines.
How do I show two lines are skew?
Skew lines in 3 dimensions are those which are not parallel and do not intersect. Let's take two example lines: l 1 = (2, 2, -1) + λ (3, 1, -3) and l 2 = (1, 0, 1) + µ (6, -4, 9)
How do you know if a diagram is skew?
Skew lines can only appear in 3-D diagrams, so try to imagine the diagram in a room instead of on a flat surface. Try imagining pulling a window shade from one line to the other. If you have to twist the shade to line it up, then the lines are skew.
How do you test for skewness in geometry?
Testing for skewness. If each line in a pair of skew lines is defined by two points that it passes through, then these four points must not be coplanar, so they must be the vertices of a tetrahedron of nonzero volume. Conversely, any two pairs of points defining a tetrahedron of nonzero volume also define a pair of skew lines.
What are skew lines and parallel lines in math?
What are Skew Lines? Skew lines are lines that are in different planes, they are never parallel, and they never intersect. On the other hand, parallel lines are lines that are in the same plane and never intersect. In other words, Parallel lines must exist in two dimensions; they are parallel within the same plane.

What is skew lines with examples?
In three-dimensional geometry, skew lines are two lines that do not intersect and are not parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron.
What is skew lines in math?
Two or more lines which have no intersections but are not parallel, also called agonic lines. Since two lines in the plane must intersect or be parallel, skew lines can exist only in three or more dimensions.
What makes a line skew?
Skew lines are two or more lines that do not intersect, are not parallel, and are not coplanar. (Remember that parallel lines and intersecting lines lie on the same plane.) This makes skew lines unique – you can only find skew lines in figures with three or more dimensions.
How do you identify parallel lines and skew lines?
1:152:28Parallel and Skew Lines - YouTubeYouTubeStart of suggested clipEnd of suggested clipBecause they're not coplanar they're not in the same plane. So on your true and false question whenMoreBecause they're not coplanar they're not in the same plane. So on your true and false question when they say a parallel line parallel lines are two lines that never intersect.
What is skew lines in graph?
Skew lines are lines that are in different planes, they are never parallel, and they never intersect. On the other hand, parallel lines are lines that are in the same plane and never intersect.
What is skew angle?
Skew angle refers to the angle at which a beam from a terminal location hits the satellite. Skew angle mitigation allows a terminal to take advantage of high skew situations while ensuring compliance with adjacent satellite interference limits.
How do you find where two lines intersect?
How Do I Find the Point of Intersection of Two Lines?Get the two equations for the lines into slope-intercept form. ... Set the two equations for y equal to each other.Solve for x. ... Use this x-coordinate and substitute it into either of the original equations for the lines and solve for y.More items...
Which are skew lines A and B?
Skew lines are noncoplanar and do not intersect. Line a lies in plane Q and line b lies in plane R, so the lines are not coplanar. No other plane can be drawn through the lines, so they are not parallel. So, a and b are skew.
Do skew lines have same slope?
Two or more lines that lie in the same plane and never intersect. Parallel lines will always have the same slope. Skew lines are lines that are in different planes and never intersect.
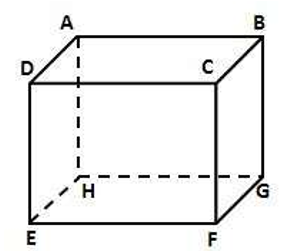
How many skew lines are in a cube?
In the cube shown, and are examples of two lines that are skew. You can verify this by checking the conditions for skew lines. and do not intersect. and do not lie on the same plane.
What does skew the results mean?
Skewness refers to a distortion or asymmetry that deviates from the symmetrical bell curve, or normal distribution, in a set of data. If the curve is shifted to the left or to the right, it is said to be skewed.
What is a skew segment?
In Geometry, skew segments are segments of skew lines, where skew lines are lines that do not lie on the same plane, and they also never intersect.
Can a line and a plane be skew?
In 2 dimensions, lines and line segments that do not intersect are inherently parallel, but in the third dimension they can be skew, so that they fit neither description.
Can skew lines be perpendicular?
Skew lines are never in the same plane. Skew lines can be perpendicular.
How do you know if a line is skew?
Skew lines are not parallel and they do not intersect. Compare the 3-d slopes of two lines to check if they are parallel, and use algebra to check...
Are skew lines parallel planes?
A plane is defined by three points, while a line is defined by two. A single line, then, can be in any number of different planes. By definition, t...
How do you know if two lines are skew?
In 3-D space, two lines must be one of these things: parallel, intersecting, or skew. If it can be proven that they are not parallel and they are n...
How to find skew lines?
When given a figure or real-world examples, to find a pair of skew lines, always go back to the definition of skew lines. Ask the following questions:
What are two examples of skew lines?
In the cube shown, A B and E H are examples of two lines that are skew. You can verify this by checking the conditions for skew lines.
What are other skew lines’ definitions?
Now, we can take a quick look into another definition of skew lines in higher mathematics.
What are parallel lines?
Parallel Lines – these are lines that lie on the same plane but never meet. Intersecting Lines – these are lines that lie on the same plane and meet. Coplanar Lines – these are lines that lie on the same plane. What if we have lines that do not meet these definitions? This is why we need to learn about skew lines.
Can skew lines be parallel?
Below are three possible pairs of skew lines. As shown in the three examples, as long as the lines are not coplanar, do not intersect, and are not parallel, they can be considered skew lines. Example 6.
Do skew lines exist in the world?
Since skew lines are found in three or more dimensions, our world will definitely contain skew lines. Here are some examples to help you better visualize skew lines:
Can you find skew lines in figures?
This makes skew lines unique – you can only find skew lines in figures with three or more dimensions.
What are Skew Lines?
Skew lines are lines that are in different planes, are not parallel, and do not intersect. Parallel lines, as you will recall, are lines that are in the same plane and do not intersect. Also, remember that in mathematics, lines extend forever in both directions.
How to tell if window shade lines are skew?
Try imagining pulling a window shade from one line to the other. If you have to twist the shade to line it up, then the lines are skew.
How to find the vector perpendicular to two lines?
Obtain the cross product vector of the direction vectors of the two lines. This vector will be the vector perpendicular on both lines. 2. Identify two parallel planes that contain the two skew lines by using an arbitrary point on each line and the vector obtained in 1. 3.
What happens if you draw a horizontal line on a wall?
If you draw another horizontal line on the wall to your right, the two lines will be parallel. If you draw any non-horizontal line on your right, then the left and right lines will be skew lines. The following is an illustration of this scenario of skew lines. Let's think about a larger example.
Do parallel lines intersect?
Parallel lines are in the same plane and do not intersect. Skew lines can only appear in 3-D diagrams, so try to imagine the diagram in a room instead of on a flat surface. Try imagining pulling a window shade from one line to the other. If you have to twist the shade to line it up, then the lines are skew.
Can FE be skew?
Any edges that intersect the line FE cannot be skew. Therefore, ED, EH, FG, and FA are not skew. Any edges that are parallel to line FE cannot be skew. Therefore, we can eliminate DG, BC, and AH. That leaves us with the lines DC, BG, HC, and AB, each of which is skew to line FE.
What are Skew Lines?
Skew lines are lines that are in different planes, they are never parallel, and they never intersect. On the other hand, parallel lines are lines that are in the same plane and never intersect.
How to find skew lines in elevator?
Inside the elevator, you realize you are looking at 12 edges (where planes intersect): Select any edge. Then select another edge that is: Do those two things, and you have found skew lines! The top, horizontal line of the elevator, for example, is skew to either rear, vertical line.
How to check if a straight edge is skew?
You can perform a quick check of suspected skew lines just with your straightedge. Align it on one line and physically move it to the other line. If you have to twist, turn, rotate or otherwise change the orientation of your straightedge to align with the second line, then the two lines are skew.
What if you wanted to hold rays or lines?
What if, though, you wanted to hold rays, or lines? No box exists that could hold either, because rays continue in one direction forever, and lines continue in two directions forever. Skew lines are what you would have if you tried to store lines in a big box.
How to tell if a bed sheet is skew?
Another way to test it is to think of hanging wet bed linens from one line to the other. If you can imagine hanging a bed sheet between the two lines so the bed sheet hangs completely flat (like a plane), the two lines are not skew. If the bed sheet has to twist, the two lines are skew.
Where is the line in an elevator?
Get more dramatic: a line from a top corner of the elevator to an opposite, bottom corner -- slicing right through the center space of the elevator (where you are standing) -- is skew to the two vertical wall corners untouched by the line.
Do parallel lines exist in two dimensions?
In other words, Parallel lines must exist in two dimensions; they are parallel within the same plane. Skew lines cannot exist in two dimensions and are always in different, non-intersecting planes.
What happens when three skew lines meet?
If three skew lines all meet three other skew lines, any transversal of the first set of three meets any transversal of the second set.
Which type of surface has two families of skew lines?
A third type of ruled surface is the hyperbo lic paraboloid. Like the hyperboloid of one sheet, the hyperbolic paraboloid has two families of skew lines; in each of the two families the lines are parallel to a common plane although not to each other.
What happens if you choose 4 points in a cube?
If four points are chosen at random uniformly within a unit cube, they will almost surely define a pair of skew lines. After the first three points have been chosen, the fourth point will define a non-skew line if, and only if, it is coplanar with the first three points. However, the plane through the first three points forms a subset of measure zero of the cube, and the probability that the fourth point lies on this plane is zero. If it does not, the lines defined by the points will be skew.
What is skew flat?
As with lines in 3-space, skew flats are those that are neither parallel nor intersect. In affine d -space, two flats of any dimension may be parallel. However, in projective space, parallelism does not exist; two flats must either intersect or be skew.
Why are the lines through segment AD and segment B 1 B skew lines?
Rectangular parallelepiped. The line through segment AD and the line through segment B 1 B are skew lines because they are not in the same plane.
Do lines in three dimensional space always form skew lines?
Therefore, any four points in general position always form skew lines.
Is the cross product of b and d perpendicular to the lines?
The cross product of b and d is perpendicular to the lines, as is the unit vector
What is skew line?
Answer: The skew lines are those lines which do not intersect, but also never lie on a similar plane. They look like they are running in similar directions and even look totally random.
What is the shortest distance between skew lines?
The shortest distance between skew lines is equal to the length of the perpendicular between the two lines. This lesson lets you understand the meaning of skew lines and how the shortest distance between them can be calculated. We will look at both, Vector and Cartesian equations in this topic. Let’s Begin!
What is the objective of skew lines?
The objective is to find out how to measure the distance between such skew lines. Note that in case the two skew lines are intersecting, the shortest distance between them must necessarily be zero. The other cases are that of parallel lines and skew lines. Skew Lines are basically, lines that neither intersect each other nor are they parallel ...
What is the difference between parallel lines and skew lines?
Answer: The most common difference between the parallel lines and the skew lines is that the parallel lines lie in a similar plane whereas the skew lines lie in dissimilar planes.
What is a line in 3D geometry?
One of the key elements of three-dimensional geometry is the straight line , also sometimes simply referred to as a line. There can be various ways in which two lines are related in the three-dimensional space.
Can skew lines be perpendicular?
Answer: A line is said to be perpendicular to the other line only if they are intersecting at a right angle, and we know that the skew lines never intersect or meet, so, the skew lines can never become a perpendicular.
