How do you find the side lengths of a 30 60 90 Triangle? Divide the hypotenuse by 2 to find the short side. Multiply this answer by the square root of 3 to find the long leg.
What is the formula for a 30 60 90 triangle?
In a 30-60-90 triangle, the ratio of the sides is always in the ratio of 1:√3: 2. This is also known as the 30-60-90 triangle formula for sides. y:y√3:2y. Let us learn the derivation of this ratio in the 30-60-90 triangle proof section. Consider some of the examples of a 30-60-90 degree triangle with these side lengths:
What are the 30 60 90 triangle rules?
What is the 30 60 90 triangle rule? In a 30°−60°−90° triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is √3 times the length of the shorter leg. To see why this is so, note that by the Converse of the Pythagorean Theorem, these values make the triangle a right triangle.
What are the properties of a 30 60 90 triangle?
The key characteristic of a 30-60-90 right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads). The sides of a 30-60-90 right triangle lie in the ratio 1:√3:2.
What is the ratio for a 30 60 90 triangle?
The ratio of the sides follow the 30-60-90 triangle ratio: 1 : 2 : √3 1 : 2 : 3. Short side (opposite the 30 30 degree angle) = x x. Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x. Long side (opposite the 60 60 degree angle) = x√3 x 3.
What are the side lengths of a 30 60 90?
30°-60°-90° Triangles There is a special relationship among the measures of the sides of a 30°−60°−90° triangle. A 30°−60°−90° triangle is commonly encountered right triangle whose sides are in the proportion 1:√3:2. The measures of the sides are x, x√3, and 2x.
How do you find the side lengths of a 30 60 90 triangle when given the hypotenuse?
0:372:44How to determine the legs of a 30 60 90 triangle when given ... - YouTubeYouTubeStart of suggested clipEnd of suggested clipYou multiply by two. So if you're given the hypotenuse to find the short leg you have to divide byMoreYou multiply by two. So if you're given the hypotenuse to find the short leg you have to divide by two. So guys all this is is 52 square root of three divided. By two 26 square root of 3..
How do you find the length of the hypotenuse of a 30 60 90 right triangle whose shorter leg is 8?
Find the lengths of the other two sides of the triangle given that one of its angles is 30 degrees. This is must be a 30°-60°-90° triangle. Therefore, we use the ratio of x: x√3:2x. Diagonal = hypotenuse = 8cm.
How do you find the missing side of a triangle?
0:1629:56How To Calculate The Missing Side Length of a Triangle - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd we have two sides of the right triangle to find the missing side we could use something calledMoreAnd we have two sides of the right triangle to find the missing side we could use something called the pythagorean theorem which states that a squared plus b squared is equal to c squared.
What is the ratio of a 30 60 90 triangle?
The most important rule to remember is that this special right triangle has one right angle and its sides are in an easy-to-remember consistent relationship with one another - the ratio is a : a√3 : 2a. Also, the unusual property of this 30 60 90 triangle is that it's the only right triangle with angles in an arithmetic progression.
What is the second leg length of a triangle?
Did you notice that our triangle of interest is simply a half of the equilateral triangle? If you remember the formula for the height of such a regular triangle, you have the answer what's the second leg length. It's equal to side times a square root of 3, divided by 2:
What is the red triangle?
Triangles (set square). The red one is the 30-60-90 degree angle triangle
How many triangle rules are there?
You read about 30 60 90 triangle rules. Now it's high time you practiced!
What is the area of a leg?
area is 34.9 in² - it's the result of multiplying the legs length and dividing by 2 area = a²√3 ≈ 34.9 in
Can you find the third side of a 30 60 90 triangle?
However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given.
What is the length of a 30-60 90 triangle?
Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5/√3 inches long.
What is the angle of an isosceles right triangle?
As these two angles are equal (the triangle being isoceles), each of the angle is 90o2=45o . Hence, an isosceles right triangle always a 45o−45o−90o triangle.
How to find the short side of a hypotenuse?
Divide the hypotenuse by 2 to find the short side. Multiply this answer by the square root of 3 to find the long leg. Type 3: You know the long leg (the side across from the 60-degree angle). Divide this side by the square root of 3 to find the short side.
What is 30-60 90?
What is a 30-60-90 Triangle? A 30-60-90 triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle). Because the angles are always in that ratio, the sides are also always in the same ratio to each other.
Which angle is the hypotenuse of a triangle always opposite?
The hypotenuse of the triangle is always opposite the right angle.
What is the sum of the squares of the two smaller sides of the triangle?
Pythagoras' theorem states that in a right triangle(or right-angled triangle) the sum of the squares of the two smaller sides of the triangleis equal to the square of the hypotenuse.
How to measure an angle with a protractor?
How to measure an angle with a protractor: Place the midpoint of the protractor on the VERTEX of the angle. Line up one side of the angle with the zero line of the protractor (where you see the number 0). Read the degrees where the other side crosses the number scale.
What is a 30-60 90 degree triangle?
A 30-60-90 degree triangle is a special right triangle, so it's side lengths are always consistent with each other. The ratio of the sides follow the 30-60-90 triangle ratio:
How many triangles are there in 50 inches?
Did you say 50 inches 50 i n c h e s? This is really two 30-60-90 triangles, which means hypotenuse M A M A is also 100 inches 100 i n c h e s, which means the shortest leg M H M H is 50 inches 50 i n c h e s.
What is the warning flag for 30-60-90 triangles?
Another warning flag with 30-60-90 triangles is that you can become so engrossed in the three properties that you lose sight of the triangle itself. It is still a triangle, so its interior angles must add to 180° 180 °, and its three sides must still adhere to the Pythagorean Theorem: a2 + b2 = c2 a 2 + b 2 = c 2.
What is the side opposite the right angle called?
In a right triangle, recall that the side opposite the right angle (the largest angle) is called the hypotenuse (the longest side, and the other two sides are called legs.
What is 30-60 90?
What is a 30-60-90 Triangle? A 30-60-90 triangle is a right triangle where the three interior angles measure 30° 30 °, 60° 60 °, and 90° 90 °. Right triangles with 30-60-90 interior angles are known as special right triangles. Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides.
What is the missing angle of a hypotenuse?
The missing angle measures 60° 60 °. It follows that the hypotenuse is 28 m 28 m , and the long leg is 14 m * √3 14 m * 3.
How long is a right triangle?
A right triangle has a short side with a length of 14 meters 14 m e t e r s with the opposite angle measuring 30° 30 °. What are the other two lengths?
30 60 90 right triangle theorem
We can define three fundamental properties and characteristics to understand the triangle theorem 30-60-90. These properties are also explicitly described for right triangles. The first property states that the longest side of a triangle called the hypotenuse in practice, always has a value twice as long as the shorter leg.
30 60 90 triangle ratio
When determining the 30-60-90 triangle theorem it is essential to know the ratio of the sides of the triangle 30-60-90. Since this is a particular type of right triangle, you must always align the lengths of the sides of the triangle, so the ratio of 30-60-90 triangles has the following appearance:
30 60 90 triangle formula
From the geometric point of view, the formula used for the calculation lies in the basics of trigonometry. If we want to calculate page lengths, we can use a sine angle of 30 degrees. According to the attached graph, we can calculate the value of the lengths of pages b and c using several formulas:
30 60 90 triangle rules and properties
When it comes to the rules you can apply in the 30-60-90 triangle, you will probably manipulate the values of the hypotenuse and the shorter legs of the triangle. The geometry is behind all these links and connections between all three sides of the triangle, and you can see what it looks like in the table below:
How do we solve a 30 60 90 triangle? – example
Let us give you more detailed explanations for the formulas for calculating each of the cases listed below, and then we will apply those same formulas to one case study.
What is a 30-60 90 triangle?
A 30-60-90 triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees. Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another.
How many degrees are there in a 30-60 90 triangle?
They're most definitely congruent. Now that we've proven the congruencies of the two new triangles, we can see that the top angles must each be equal to 30 degrees (because each triangle already has angles of 90° and 60° and must add up to 180°). This means we have made two 30-60-90 triangles.
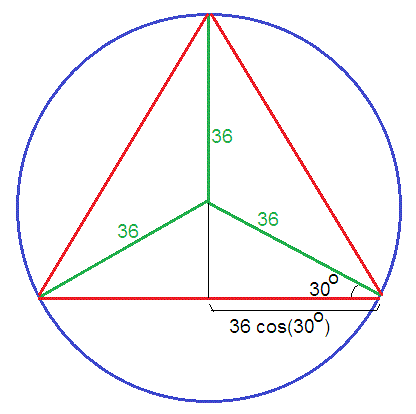
How many angles does an equilateral triangle have?
Because a triangle's interior angles always add up to 180° and. 180. 3. = 60, an equilateral triangle will always have three 60° angles. Now let's drop down a height from the topmost angle to the base of the triangle. We've now created two right angles and two congruent (equal) triangles.
What is the hypotenuse of a right triangle?
We can see that this is a right triangle in which the hypotenuse is twice the length of one of the legs. This means this must be a 30-60-90 triangle and the smaller given side is opposite the 30°. The longer leg must, therefore, be opposite the 60° angle and measure 6 * √ 3, or 6 √ 3.
How do we know if a triangle is equal?
How do we know they're equal triangles? Because we dropped a height from an equilateral triangle, we've split the base exactly in half. The new triangles also share one side length (the height), and they each have the same hypotenuse length. Because they share three side lengths in common (SSS), this means the triangles are congruent.
What are the different types of triangles?
Acute, obtuse, isosceles, equilateral …When it comes to triangles, there are many different varieties, but only a choice few that are "special.". These special triangles have sides and angles which are consistent and predictable and can be used to shortcut your way through your geometry or trigonometry problems.
What is the third measure of a hypotenuse?
Again, we are given two angle measurements (90° and 60°), so the third measure will be 30°. Because this is a 30-60-90 triangle and the hypotenuse is 30, the shortest leg will equal 15 and the longer leg will equal 15√3.