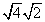
Simplifying Radical Expressions with Cube Root or Higher Root
- Determine the prime factors of the number under the root.
- Write the prime factors in groups.
- Simplify any multiplication and exponents.
- Simplify the radical until no further simplification can be done. The process of simplifying radical expressions with variables is similar to that of numbers.
How to simplify a radical to give an exact answer?
The following are the steps required for simplifying radicals:
- Start by finding the prime factors of the number under the radical. ...
- Determine the index of the radical. ...
- Move only variables that make groups of 2 or 3 from inside to outside radicals.
- Simplify the expressions both inside and outside the radical by multiplying.
- Simplify by multiplication of all variables both inside and outside the radical.
How do you solve radicals step by step?
- Original Equation: x = 2 x + 3 {\displaystyle {\sqrt {x}}=2x+3}
- Square both sides: ( x) 2 = ( 2 x + 3) 2 {\displaystyle ( {\sqrt {x}})^ {2}= (2x+3)^ {2}}
- Expand Expressions: x = 4 x 2 + 12 x + 9 {\displaystyle x=4x^ {2}+12x+9}
- The expression above was expanded through Polynomial Multiplication. ...
What are some ways to simplify radicals?
a. Simplify the fraction inside the radical first. Divide the like bases by subtracting the exponents. Simplify. b. Use the Quotient Property of exponents to simplify the fraction under the radical first. Simplify. Use the Quotient Property of exponents to simplify the fraction under the radical first.
How do you express in simplest radical form?
A radical expression is said to be in standard form if the following conditions hold:
- The radicand is positive.
- The radical index is as small as possible.
- The exponent of each factor of the radicand is a natural number less than the radical index.
- There are no fractions in the radicand.
- There are no radicals in the denominator of a fraction.
What are the parts of radical expressions?
A radical expression is composed of three parts: a radical symbol, a radicand, and an index. In this tutorial, the primary focus is on simplifying radical expressions with an index of 2. This type of radical is commonly known as the square root.
How to divide exponents?
Simply put, divide the exponent of that “something” by 2.
How to write the final answer?
The standard way of writing the final answer is to place all the terms (both numbers and variables) that are outside the radical symbol in front of the terms that remain inside.
What is the square root of the product of a and b?
This means that the square root of the product of a and b is equal to the product of their individual square roots.
How many is 400 in radicand?
For the number in the radicand, I see that 400 = 202.
Can you simplify a radicand with a perfect square factor?
It’s okay if ever you start with the smaller perfect square factors. You just need to make sure that you further simplify the leftover radicand (stuff inside the radical symbol). Repeat the process until such time when the radicand no longer has a perfect square factor.
Does radicand contain variables?
The radicand contains both numbers and variables. Let’s deal with them separately.
How to simplify fractions?
Rewrite the fraction as two radical expressions instead. Some people prefer this other method of solving problems like this. Rewrite the fraction so there is one root in the numerator and another in the denominator. Simplify each root separately, then simplify the fraction.
What exponents are left under the square root?
Since there are no other exponents left under the square root, you're all done!
What to do if you have any multiplication or exponents left?
Simplify if possible. If you have any multiplication or exponents left, calculate them so your final answer is in simplest form.
How to combine two terms into one expression?
Combine the terms using exponent rules . Once you've converted your terms to exponent form, follow the rules of exponents to combine them into a single expression.
How to make a variable positive?
Use the absolute value symbol to make a variable positive. Variables are tricky: we don't know whether they represent a positive or a negative number. Since the square root (or any even root) function must always give a positive answer, we make sure this happens by using the absolute value symbol around the answers, like this: |x|. This symbol just means "make this value positive."
How many square roots does 4 have?
both equal 4. That means that 4 (or any positive number) actually has two square roots: one positive number and one negative. But the square root symbol
Can you cancel out exponents and roots?
Cancel out exponents and roots just as you would with integers. Algebraic problems involve variables like
How to simplify radical expressions with variables?
The process of simplifying radical expressions with variables is similar to that of numbers. We factorize the variables along with the numbers. Let us consider an example of simplifying radical expressions with variables for a better understanding. Consider the radical expression √ (100x 4 y 6 z 3 ).
What is Simplifying Radical Expressions?
Simplifying radical expressions is a process of reducing the radical expressions to the simplest form and removing the radical completely, if possible. If a radical expression is present in the denominator of an algebraic expression, we multiply the numerator and denominator with the appropriate radical expression (for example, conjugate in case of a binomial, and the same radical in case of a monomial) for simplifying the radical expression.
What is the process of eliminating radicals?
Simplifying radical expressions is a process of eliminating radicals or reducing the expressions consisting of square roots, cube roots, or in general, nth root to simplest form.
What is the meaning of radical expressions in algebra?
Simplifying radical expressions in algebra is a concept in algebra where we simplify an expression with a radical into a simpler form and remove the radical, if possible . Let us now recall the meaning of radical expressions. Radical expressions are algebraic expressions involving radicals. The radical expressions consist of the root of an algebraic expression (number, variables, or combination of both). The root can be a square root, cube root, or in general, n th root. Simplifying radical expressions implies reducing the algebraic expressions to the simplest form and, if possible, completely eliminating the radicals from the expressions.
What are the mathematical concepts that simplify radical expressions?
All mathematical concepts including addition, subtraction, multiplication, and division are important in simplifying radical expressions along with the order of operations.
When to use absolute value in radical expressions?
The even power of any number is always positive, therefore any even-numbered root must be a positive number (otherwise it is imaginary), and hence the absolute value must be used when simplifying radical expressions with variables, which ensures the answer is positive. When working with radical expressions with odd radicals, this requirement does not apply because odd roots exist for negative numbers.
Is the square root of a negative number always non-negative?
Since the square of a negative number is the same as the square of the positive number with the same magnitude, therefore we need to remember that the square root of a number will always be non-negative. Hence we take the absolute value.
What is simplifying radicals?
Simplifying radicals is the process of manipulating a radical expression into a simpler or alternate form. Generally speaking, it is the process of simplifying expressions applied to radicals.
When multiplying radicals, do we make extensive use of the identity#N#a b?
When multiplying radicals, we make extensive use of the identity#N#a b = a × b#N#sqrt {ab}=sqrt {a}timessqrt {b} ab#N##N#= a#N##N#× b#N##N#. This means that two radicals, when multiplied together, might produce an integer rather than another radical.
When to use difference of two squares identity?
However, when the denominator is a binomial expression involving radicals, we can use the difference of two squares identity to produce a conjugate pair that will remove the radicals from the denominator. For example, if we want to remove the radicals from the expression. . . 1 + 5 2. − 1 + 5 2.
When are roots of higher degree simplified?
Similarly, roots of higher degree (cube roots, fourth roots, etc.) are simplified when they have no factors under the radical that are perfect powers of the same degree as the radical.
Can identity be applied to radical multiplication?
This will not always happen; however, the identity used above can be applied even to more complicated radical multiplication.
Can radicals be simplified?
Since they are exponents, radicals can be simplified using rules of exponents.
Can radicals be added together?
Since radicals are actually exponential expressions, they follow the rules of exponents and cannot be added together. In particular, you should avoid the common mistake shown below:
What is the simplest form of a radical?
Your radical is in the simplest form when the radicand cannot be divided evenly by a perfect square. Radicals ( or roots ) are the opposite of exponents. For instance, 3 squared equals 9, but if you take the square root of nine it is 3. For example. 4^2=16 and √16 =4. 2^3=8 and ∛8 = 2. 3^3= 27 and ∛27=3.
How to make a radical a square root?
Step 1 Create a factor tree. Step 2 When the radical is a square root any like pair of numbers escape from under the radical. In this example the pair of 5’s escape and the 3 remains under the radical. √ ( 5 5 3) the 5’s jailbreak and escape in a pair and the three remains under the radical. 5√3. Simplify √96. Step 1.
What is a radical symbol?
Radical symbol. The symbol that looks like a check mark. √ The bar tells you how much of the value to use. You can think of the bar as parenthesis. For example,
What is the check mark in a radicand?
The check mark √ is called the radical symbol and gives you three pieces of important information, the degree, the radical symbol, and the radicand.
How to simplify a square root?
In order to simplify a square root you take out anything that is a perfect square.
Is a degree of 3 a cube root?
A degree of 3 is a cube root , a 4 is the fourth root. Most times for a square root a degree will be missing, and it is assumed that it is a square root.
What is a radical in simplest form?
Fractional radicand. W E SAY THAT A SQUARE ROOT RADICAL is simplified, or in its simplest form, when the radicand has no square factors. A radical is also in simplest form when the radicand is not a fraction. Example 1. 33, for example, has no square factors.
Why does 42 have no square factors?
We now see that 42 has no square factors -- because no factor is repeated. Compare Example 1 and Problem 2 of the previous Lesson.
Can a radical be reduced?
The radical is in its simplest form. The fraction cannot be reduced.
Does the 7th equinox belong to any radical?
As for 7, it does not " belong" to any radical.
Is radicand simplified?
is now simplified. The radicand no longer has any square factors.
What is the property of radicals?
It says that the square root of a product is the same as the product of the square roots of each factor. When you write a radical, you want to make sure that the number under the square root sign doesn't have any factors that are perfect squares.
What are the rules for simplifying fractions?
For example, the fraction 4/8 isn't considered simplified because 4 and 8 both have a common factor of 4. You also wouldn't ever write a fraction as 0.5/6 because one of the rules about simplified fractions is that you can't have a decimal in the numerator or denominator.#N#There are rules that you need to follow when simplifying radicals as well. One rule is that you can't leave a square root in the denominator of a fraction. Another rule is that you can't leave a number under a square root if it has a factor that's a perfect square. If a number inside a square root has a factor of 4, 9, 16, 25, 36, 49, etc., you'll have to do some steps to simplify the radical. We'll show you how to do this next.
What is the second square root?
The second square root just has a 2 inside. 2 doesn't have any factors that are perfect squares other than 1, so that part we just leave as it is since it can't be simplified any more. Think about the factors of 63. Start with the smallest perfect square and work your way up.
Can you leave a square root in a fraction?
One rule is that you can't leave a square root in the denominator of a fraction. Another rule is that you can't leave a number under a square root if it has a factor that's a perfect square. If a number inside a square root has a factor of 4, 9, 16, 25, 36, 49, etc., you'll have to do some steps to simplify the radical.
Is 7 a radical?
7 doesn't have any factors that are perfect squares other than 1, so it's left under the radical sign. You can also simplify radicals with variables under the square root. You'll want to split up the number part of the radicand just like you did before, but you'll also split up the variables too.