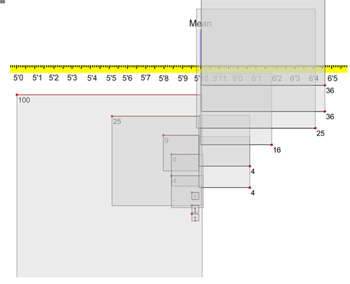
The more variable the population, the greater the uncertainty in our estimate. Similarly, the larger the sample size the more information we have and so our uncertainty reduces. Suppose that we want to estimate the proportion of adults who own a smartphone in the UK. We could take a sample of 100 people and ask them.
What happen to the variance if sample size increases?
What happens to the variance if sample size increases? The variance of the sample will remain about the same, but with some random variation. After all, it is an estimate of the variance of the population. Originally Answered: what happen to the variance If sample size increases ?
What is sampling variability?
This variation from sample to sample in the values of the sample statistic is called sampling variability . The previous lesson investigated the statistical question, “What is the typical time spent at the gym?” by selecting random samples from the population of 800 gym members.
Does sample size affect validity or reliability?
Does sample size affect reliability or validity? A small sample size affects the reliability of a survey's results because it leads to a higher variability, which may lead to bias. Because say you have a population and you are trying to find the different ages of a population, and a sample you take is totally random.
How do you find the variance of the sample mean?
If \sigma^2 is the variance of the population from where sampling is undertaken, then variance of the sample mean is \sigma^2/n where n is the sample size and sampling is with replacement. Hence the variance of the sample mean decreases as n increases and vice versa. What are the tricks that corporate America uses to get us to spend more money?

How can variability affect a sample?
Variability and Sample Sizes Increasing or decreasing sample sizes leads to changes in the variability of samples. For example, a sample size of 10 people taken from the same population of 1,000 will very likely give you a very different result than a sample size of 100.
Does bigger sample size mean more variability?
The mean of the sample means would be very close to μ, the mean for the population from which the samples were drawn. However, the variability in the sample means will depend on the size of the samples, since larger samples are more likely to give estimated means that are closer to the true mean of the population.
How does sample size affect bias and variability?
Increasing the sample size tends to reduce the sampling error; that is, it makes the sample statistic less variable. However, increasing sample size does not affect survey bias. A large sample size cannot correct for the methodological problems (undercoverage, nonresponse bias, etc.) that produce survey bias.
How does the variability in the population impact the sampling distribution?
Sampling variability will decrease as the sample size increases. A parameter is a fixed number that describes a population, such as a percentage, proportion, mean, or standard deviation. In reality, we do not know these numbers because we cannot examine the entire population.
Why is variability in sampling important?
– Variability measures how well an Variability measures how well an individual score (or group of scores) represents the entire distribution. This aspect of variability is very important for inferential statistics where relatively small samples are used to answer questions about populations populations.
Is there more variability in smaller samples?
If there is an increased probability of one small sample being unusual, that means that if we were to draw many small samples as when a sampling distribution is created (see the second lecture), unusual samples are more frequent. Consequently, there is greater sampling variability with small samples.
What is sample sample variability?
Sampling variability refers to the fact that the mean will vary from one sample to the next. For example, in one random sample of 30 turtles the sample mean may turn out to be 350 pounds. In another random sample, the sample mean may be 345 pounds. In yet another sample, the sample mean may be 355 pounds.
What happens when variance increases?
Standard Error is the square root of the variance. When the variance increases, so does the standard error. Since the standard error occurs in the denominator of the t statistic, when the standard error increases, the value of the t decreases.
What do you mean by variability?
What Is Variability? Variability, almost by definition, is the extent to which data points in a statistical distribution or data set diverge—vary—from the average value, as well as the extent to which these data points differ from each other.
Does population size affect variability?
Furthermore, if the population size is significantly larger than the sample size, then the size of the population will not affect the variability of the sampling distribution (i.e., a sample of size 100 from a population of size 100,000 will have the same variability as a sample of size 100 from a population of size ...
What is the variability in a sampling distribution?
The variability of a sampling distribution is measured by its variance or its standard deviation. The variability of a sampling distribution depends on three factors: N: The number of observations in the population. n: The number of observations in the sample.
How does variability affect data collection?
Variability (also called spread or dispersion) refers to how spread out a set of data is. Variability gives you a way to describe how much data sets vary and allows you to use statistics to compare your data to other sets of data.
Which sample has more variability?
Sample AAlthough the data follows a normal distribution, each sample has different spreads. Sample A has the largest variability while Sample C has the smallest variability.
What happens to mean when sample size increases?
Therefore, as a sample size increases, the sample mean and standard deviation will be closer in value to the population mean μ and standard deviation σ .
What is the effect of increasing sample size?
Because we have more data and therefore more information, our estimate is more precise. As our sample size increases, the confidence in our estimate increases, our uncertainty decreases and we have greater precision.
Why would we want a variability estimate based on a larger sample to count more to be more heavily weighted than one based on a smaller sample?
Why would we want the variability estimate based on a large sample to count more (to be more heavily weighted) than one based on a smaller sample? Variability estimated based on a larger sample would be more accurate and reliable than one based on a smaller sample which can vary more.
When is there less variability among samples?
In other words, there is less variability among sample means when the sample sizes are larger.
What is sampling variability?
Sampling variability refers to the fact that the mean will vary from one sample to the next.
How many samples are needed to estimate a population parameter?
In practice, we only collect one sample to estimate a population parameter. For example, we will only collect one sample of 30 sea turtles to estimate the mean weight for the entire population of turtles.
What is the property of standard deviation?
One interesting property of the standard deviation of the sample mean is that it naturally becomes smaller as we use larger and larger sample sizes.
What happens to the sample size as the sample size increases?
As a sample size increases, sample variance (variation between observations) increases but the variance of the sample mean (standard error) decreases and hence precision increases.
What is the variability that shrinks when N increases?
The variability that's shrinking when N increases is the variability of the sample mean , often expressed as standard error. Or, in other terms, the certainty of the veracity of the sample mean is increasing.
What is the variance of the mean?
This means that with n independent (or even just uncorrelated) variates with the same distribution, the variance of the mean is the variance of an individual divided by the sample size.
What is the variance of a sum of variables?
In fact, when you're dealing with uncorrelated random variables, we can say something more specific: the variance of a sum of variates is the sum of their variances. This means that with n independent (or even just uncorrelated) variates with the same distribution, the variance of the mean is the variance of an individual divided by the sample size.
Why is the bell shape narrower when each sample is large?
In other words, the bell shape will be narrower when each sample is large instead of small, because in that way each sample mean will be closer to the center of the bell. Share.
What is standard error in statistics?
That standard error is representing the variability of the means or effects in your calculations. The smaller it is, the more powerful your statistical test.
What should the average of the results obtained from a large number of trials be?
According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.
Is the variance of a sample the same?
The variance of the sample will remain about the same , but with some random variation. After all, it is an estimate of the variance of the population.
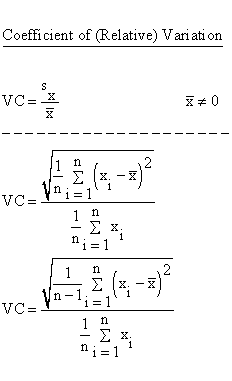
Is sqrt of variance equal to SD?
you know that sqrt of variance is equal to SD.
What happens to the power of the test when the sample size gets larger?
As the sample size gets larger, the z value increases therefore we will more likely to reject the null hypothesis ; less likely to fail to reject the null hypothesis, thus the power of the test increases.
When we conduct a two-sample t test for testing equal mean on both cases, would the statistic?
When we conduct a two-sample t test for testing equal mean on both cases, case 1’s test statistic would be much larger than case 2’s test statistic; we will have less type 2 error for case 1 thus the higher power.
What is the power of a statistical test?
It is to determine a sample size required to discover an effect size, a measure of a change or a difference that are being tested, with a given degree of confidence. That means that the power (1- a type II error) of a statistical test involves with a sample size, a type I error, and an effect size.
How is effect size related to power?
An effect size is closely related to a power of a statistical test because when “difference” of two groups is big, it is “easy” to reject the null hypothesis.
Is effect size a good measure of effectiveness?
It is a good measure of effectiveness of an intervention. For example, if we conduct a study about improving cholesterol levels for a group of people, we could calculate an effect size for before/after different methods like diet, different types of exercise etc. are applied.
Is the t statistic proportional to the standard error?
Now, we can see that the t-statistic is inversely proportional to the standard error/variance of the sample population ( σ / n ). Higher n leads to smaller standard error that gives higher t-value. Higher t-value means lower p-value infering that the difference between sample-mean ( X ¯) and population-mean ( μ) is significant (hence we reject the null hypothesis).
Is the sample from a population that has the same mean as the population it is being compared to?
but this is true only if the sample is from a population that has the same mean as the population it is being compared to. The word "population" is being used to refer to two different populations