Who was the creator of Pascal's triangle?
The triangle was first given the name, "Pascal's triangle," by a mathematician named Montmort in 1708. Montmort wrote the numbers in the form below known as the combinatorial triangle.
Who is the inventor of isosceles triangle?
In the world of geometry, there are many types of triangles besides isosceles:
- Right triangles are triangles that have one right angle equaling 90 degrees.
- Scalene triangles are triangles with no equal sides.
- Acute triangles are triangles where all three angles are less than 90 degrees.
- Obtuse triangles have one angle that is greater than 90 degrees.
- Equilateral triangles are triangles with three equal sides and angles.
Who invented the first triangles?
- … my period is <whenever>
- …I’m still lactating.
- … she's too pretty to have <sexually-transmitted disease>
Who invented the try square?
Who invented the try square? Albert J. Swanson invented the A Speed Square in 1925 as a carpenter's layout tool. He later founded Swanson Tool Company, Inc. to produce it.

How did Blaise Pascal invented Pascal's triangle?
The triangle is constructed by starting with a 1 in the upper left corner and each number in the triangle is a result of adding the number to its left to the number above it. Pascal used this triangle to conclude many results. One of these is his solution of the division problem.
Why was the Pascal's triangle created?
In 1653, a French mathematician-philosopher named Blaise Pascal described a triangular arrangement of numbers corresponding to the probabilities involved in flipping coins, or the number of ways to choose 'n' objects from a group of 'm' indistinguishable objects. Pascal's triangle has many uses in binomial expansions.
Did Blaise Pascal invent the triangle?
Pascal's Triangle is a special triangular arrangement of numbers used in many areas of mathematics. It is named after the famous 17 th century French mathematician Blaise Pascal because he developed so many of the triangle's properties.
How is Pascal's triangle used in real life?
The numbers we acquire in each stage are the sum of the two numbers above. Probability and combinations are two real-life applications of Pascal's Triangle. Architects, graphic designers, banking, and mapping are examples of where Pascal's Triangle is used.
Who invented Pascal?
Pascaline, also called Arithmetic Machine, the first calculator or adding machine to be produced in any quantity and actually used. The Pascaline was designed and built by the French mathematician-philosopher Blaise Pascal between 1642 and 1644.
What did Pascal invented?
Pascal's calculatorMechanical calculatorAdding machineBlaise Pascal/Inventions
Who invented the triangle?
Chinese mathematician Jia Xian devised a triangular representation for the coefficients in the 11th century. His triangle was further studied and popularized by Chinese mathematician Yang Hui in the 13th century, for which reason in China it is often called the Yanghui triangle.
How to make a triangle in Chinese?
The triangle can be constructed by first placing a 1 (Chinese “—”) along the left and right edges. Then the triangle can be filled out from the top by adding together the two numbers just above to the left and right of each position in the triangle.
Who discovered the old method?
It was included as an illustration in Chinese mathematician Zhu Shijie ’s Siyuan yujian (1303; “Precious Mirror of Four Elements”), where it was already called the “Old Method.”. The remarkable pattern of coefficients was also studied in the 11th century by Persian poet and astronomer Omar Khayyam. The triangle can be constructed by first placing ...
Who created the fractal?
Polish mathematician Wacław Sierpiński described the fractal that bears his name in 1915, although the design as an art motif dates at least to 13th-century Italy. Begin with a solid equilateral triangle, and remove the triangle formed by connecting the midpoints of each side.
What is the name of the treatise Pascal wrote on the triangle?
Pascal's Traité du triangle arithmétique ( Treatise on Arithmetical Triangle) was published posthumously in 1665. In this, Pascal collected several results then known about the triangle, and employed them to solve problems in probability theory.
What is the set of numbers that form Pascal's triangle?
The set of numbers that form Pascal's triangle were known before Pascal. However, Pascal developed many uses of it and was the first one to organize all the information together in his treatise, Traité du triangle arithmétique (1653). The numbers originally arose from Hindu studies of combinatorics and binomial numbers and the Greeks' study ...
When was the triangle of binomial coefficients first used?
The earliest explicit depictions of a triangle of binomial coefficients occur in the 10th century in commentaries on the Chandas Shastra, an Ancient Indian book on Sanskrit prosody written by Pingala in or before the 2nd century BC.
Who named the triangle?
The triangle was later named after Pascal by Pierre Raymond de Montmort (1708) who called it "Table de M. Pascal pour les combinaisons" (French: Table of Mr. Pascal for combinations) and Abraham de Moivre (1730) who called it "Triangulum Arithmeticum PASCALIANUM" (Latin: Pascal's Arithmetic Triangle), which became the modern Western name.
Who is the Italian mathematician who created the triangle?
In Italy, it is referred to as Tartaglia's triangle, named for the Italian algebraist Niccolò Fontana Tartaglia (1500–77). Tartaglia is credited with the general formula for solving cubic polynomials, (which may in fact be from Scipione del Ferro but was published by Gerolamo Cardano 1545).
Who was the first person to describe the Khayyam-Pascal triangle?
It was later repeated by the Persian poet-astronomer-mathematician Omar Khayyám (1048–1131); thus the triangle is referred to as the Khayyam-Pascal triangle or simply the Khayyam triangle in Iran.
Who created the arithmetic triangle?
The "Yang Hui's triangle" was known in China in the early 11th century by the Chinese mathematician Jia Xian (1010–1070).
Introduction
Mathematics is a world of numbers. We have different sets of numbers that can be arranged in different sequences and patterns. One such arrangement of numbers is the Pascal’s triangle. What is it and who invented it? Let us find out.
Definition
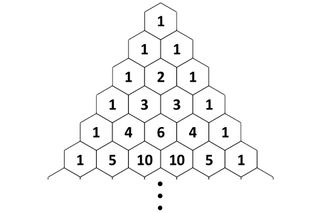
Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle. We can also say that Pascal’s triangle is an arrangement of binomial coefficients in triangular form.
Key Facts and Summary
Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle.
Recommended Worksheets
We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!
What does Pascal's triangle show?
Pascal's Triangle can show you how many ways heads and tails can combine. This can then show you the probability of any combination. For example, if you toss a coin three times, there is only one combination that will give you three heads (HHH), but there are three that will give two heads and one tail (HHT, HTH, THH), ...
What is the name of the little machine in Pascal's triangle?
The Quincunx. An amazing little machine created by Sir Francis Galton is a Pascal's Triangle made out of pegs. It is called The Quincunx . Balls are dropped onto the first peg and then bounce down to the bottom of the triangle where they collect in little bins.
What is the formula for a triangle?
In fact there is a formula from Combinations for working out the value at any place in Pascal's triangle: Notation: "n choose k" can also be written C (n,k), nCk or even nCk. The "! " is " factorial " and means to multiply a series of descending natural numbers.
How to build a triangle with numbers?
To build the triangle, start with "1" at the top, then continue placing numbers below it in a triangular pattern. Each number is the numbers directly above it added together.
What is the first diagonal?
Diagonals. The first diagonal is, of course, just "1"s. The next diagonal has the Counting Numbers (1,2,3, etc). The third diagonal has the triangular numbers. (The fourth diagonal, not highlighted, has the tetrahedral numbers .)
When was the triangle written?
It is from the front of Chu Shi-Chieh's book " Ssu Yuan Yü Chien" (Precious Mirror of the Four Elements), written in AD 1303 (over 700 years ago, and more than 300 years before Pascal!), and in the book it says the triangle was known about more than two centuries before that.
Does the formula work in Pascal's triangle?
Example: Row 4, term 2 in Pascal's Triangle is "6" ... ... let's see if the formula works: Yes, it works! Try another value for yourself. This can be very useful ... you can now work out any value in Pascal's Triangle directly (without calculating the whole triangle above it).
When was Pascal's triangle discovered?
History of Pascal’s Triangle. Blaise Pascal was born at Clermont-Ferrand, in the Auvergne region of France on June 19, 1623. In 1653 he wrote the Treatise on the Arithmetical Triangle which today is known as the Pascal’s Triangle. Although other mathematicians in Persia and China had independently discovered the triangle in the eleventh century, ...
How to explain Pascal's triangle?
Pascal’s Triangle Definition. Most people are introduced to Pascal’s triangle through an arbitrary-seeming set of rules. Begin with 1 on the top and with 1’s running down the two sides of a triangle. Each new number lies between two numbers and below them, and its value is the sum of the two numbers above it.
How to find Fibonacci numbers on a Pascal triangle?
There are various ways to show the Fibonacci numbers on the Pascal triangle. R. Knott was able to find the Fibonacci appearing as sums of “rows” in the Pascal tri angle. He moved all the rows over by one place and here the sums of the columns would represent the Fibonacci numbers.
What are the properties of Pascal's triangle?
Properties of Pascal’s Triangle 1 Each number is the sum of the two numbers above it. 2 The outside numbers are all 1. 3 The triangle is symmetric. 4 The first diagonal shows the counting numbers. 5 The sums of the rows give the powers of 2. 6 Each row gives the digits of the powers of 11. 7 Each entry is an appropriate “choose number.” 8 And those are the “binomial coefficients.”
What was Pascal's contribution to mathematics?
This triangle was among many of Pascal’s contributions to mathematics. He also came up with significant theorems in geometry, discovered the foundations of probability and calculus and also invented the Pascaline-calculator. Still, he is best known for his contributions to the Pascal triangle.
How to construct a triangle with no numbers?
The easiest way to construct the triangle is to start at row zero and write only the number one. From there , to obtain the numbers in the following rows, add the number directly above and to the left of the number with the number above and to the right of it. If there are no numbers on the left or right side, replace a zero for that missing number and proceed with the addition. Here is an illustration of rows zero to five.
How to describe a triangle?
A different way to describe the triangle is to view the first line is an infinite sequence of zeros except for a single 1. To obtain successive lines, add every adjacent pair of numbers and write the sum between and below them. The non-zero part is Pascal’s triangle.
Overview
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arise in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy.
The rows of Pascal's triangle are conventionally enumerated starting with row at the top (the 0th …
History
The pattern of numbers that forms Pascal's triangle was known well before Pascal's time. Pascal innovated many previously unattested uses of the triangle's numbers, uses he described comprehensively in the earliest known mathematical treatise to be specially devoted to the triangle, his Traité du triangle arithmétique (1654; published 1665).
Binomial expansions
Pascal's triangle determines the coefficients which arise in binomial expansions. For example, consider the expansion
.
The coefficients are the numbers in the second row of Pascal's triangle: , , .
In general, when a binomial like is raised to a positive integer power of , we have:
Combinations
A second useful application of Pascal's triangle is in the calculation of combinations. For example, the number of combinations of things taken at a time (called n choose k) can be found by the equation
.
But this is also the formula for a cell of Pascal's triangle. Rather than performing the calculation, …
Relation to binomial distribution and convolutions
When divided by , the th row of Pascal's triangle becomes the binomial distribution in the symmetric case where . By the central limit theorem, this distribution approaches the normal distribution as increases. This can also be seen by applying Stirling's formula to the factorials involved in the formula for combinations.
This is related to the operation of discrete convolution in two ways. First, polynomial multiplicatio…
Patterns and properties
Pascal's triangle has many properties and contains many patterns of numbers.
• The sum of the elements of a single row is twice the sum of the row preceding it. For example, row 0 (the topmost row) has a value of 1, row 1 has a value of 2, row 2 has a value of 4, and so forth. This is because every item in a row produces two items in the next row: one left and one right. The sum of the ele…
Extensions
Pascal's triangle has higher dimensional generalizations. The three-dimensional version is called Pascal's pyramid or Pascal's tetrahedron, while the general versions are called Pascal's simplices.
Pascal's triangle can be extended to negative row numbers.
First write the triangle in the following form:
See also
• Bean machine, Francis Galton's "quincunx"
• Bell triangle
• Bernoulli's triangle
• Binomial expansion
• Euler triangle
Introduction
- Mathematicsis a world of numbers. We have different sets of numbers that can be arranged in different sequences and patterns. One such arrangement of numbers is the Pascal’s triangle. What is it and who invented it? Let us find out.
Definition
- Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle. We can also say that Pascal’s triangle is an arrangement of binomial coefficients in triangular form. The numbers in Pascal’s triangle are placed in such a way that each number is t…
Who Invented Pascal’s Triangle?
- Blaise Pascal was born on June 19, 1623, at Clermont-Ferrand, in the Auvergne region of France. Pascal triangle as we know it today was originally written as the Treatise on the Arithmetical Triangle by Blaise Pascal in 1653. Although in the eleventh century mathematicians from Persia and China had independently discovered the triangle, most of the...
Construction of Pascal’s Triangle
- The following are the steps involved in the construction of Pascal’s triangle – 1. Starting with row zero and writing only the number one is the easiest way to construct a pascal Triangle. 2. The next step is to obtain the numbers in the subsequent rows. The pattern followed here is that we add the number directly above and to the left of the number with the number above and to the right o…
Properties of Pascal’s Triangle
- The following are the properties of a Pascal’s triangle – 1. Each digit in the Pascal’s triangle is actually the sum of the two numbers that lie above it. This number is placed between the above lying numbers in the next row. 2. The outside numbers of the Pascal’s triangle are all 1. 3. The Pascal’s triangle is symmetric in appearance due to the specific arrangement of digits. 4. The fir…
The Formula of Pascal’s Triangle
- How do we find out numbers placed on any sequence of the Pascal’s triangle? Is there any formula for it? Let us find out. Let the rows of a Pascal’s triangle be represented by “ n “ and the columns of a Pascal’s triangle be represented by “ k “. So, the formula to find the entry of an element in the nth row and kth column of a pascal’s triangle is given by – ( n k ) = ( n-1 k-1 ) + ( n …
Use of Pascal’s Triangle in Probability
- Pascal’s triangle finds its use in a number of applications in mathematics. For example, Pascal’s triangle is extensively used in Probability to find the possible number of outcomes of a given situation. For instance, the number of combinations of heads or tails that are possible from the number of process can be obtained using a Pascal’s Triangle. The below table demonstrates dif…
Pascal’s Triangle and Binomial Expansion
- The coefficients that appear in the binomials expansions can be defined by the Pascal’s triangle as well. This means the n th row of Pascal’s triangle comprises the coefficients of the expanded expression of the polynomial (x + y) n. We know that a binomial expansion is defined as – ( x + y) n = a 0 x n + a 1 x n – 1 y + a 2 x n – 2 y 2 + a 3 x n – 3 y 3 … + a n – 1 x y n – 1 + a n y n The coef…
Examples
- Example 1 Expand ( x + y )3using Pascal’s triangle. Solution Let us find the value of ( x + y )3using Pascal’s triangle. From the above we can see that the coefficient’s of the expansion ( x + y )3will be 1, 3, 3 1. Let us now verify the same using the formula of the binomial expansion. We know that – ( x + y) n = a 0 x n + a 1 x n – 1 y + a 2 x n – 2 y 2 + a 3 x n – 3 y 3 … + a n – 1 x y n – 1 + a n y n …
Key Facts and Summary
- Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle.
- Each digit in the Pascal’s triangle is actually the sum of the two numbers that lie above it. This number is placed between the above lying numbers in the next row.
- Pascal’s Triangle is the triangular arrangement of numbers that gives the coefficients in the expansion of any binomial expression. The numbers are so arranged that they reflect as a triangle.
- Each digit in the Pascal’s triangle is actually the sum of the two numbers that lie above it. This number is placed between the above lying numbers in the next row.
- The outside numbers of the Pascal’s triangle are all 1.
- The Pascal’s triangle is symmetric in appearance due to the specific arrangement of digits.