
What is the congruent angle of an isosceles right triangle?
An Isosceles Right Triangle is a right triangle that consists of two equal length legs. Since the two legs of the right triangle are equal in length, the corresponding angles would also be congruent. Thus, in an isosceles right triangle, two legs and the two acute angles are congruent.
What is the measure of 90 degrees in a right triangle?
Isosceles Right Triangle. A right triangle is a triangle in which exactly one angle measures 90 degrees. Since the sum of the measures of angles in a triangle has to be 180 degrees, it is evident that the sum of the remaining two angles would be another 90 degrees. The two perpendicular sides are called the legs of a right triangle, ...
How many degrees are there in an isosceles triangle?
Also, two congruent angles in isosceles right triangle measure 45 degrees each, and the isosceles right triangle is:
What is the perimeter of a triangle?
For a triangle, the perimeter would be the sum of all the sides of the triangle. Thus, the perimeter a triangle with side lengths a, b, and c, would be: In an isosceles right triangle, we know that two sides are congruent.
How long are congruent legs?
Therefore, the length of the congruent legs is 5√2 cm.
What is the angle between the legs of a right triangle?
Since it is a right triangle, the angle between the two legs would be 90 degrees, and the legs would obviously be perpendicular to each other.
Is a right triangle an equilateral triangle?
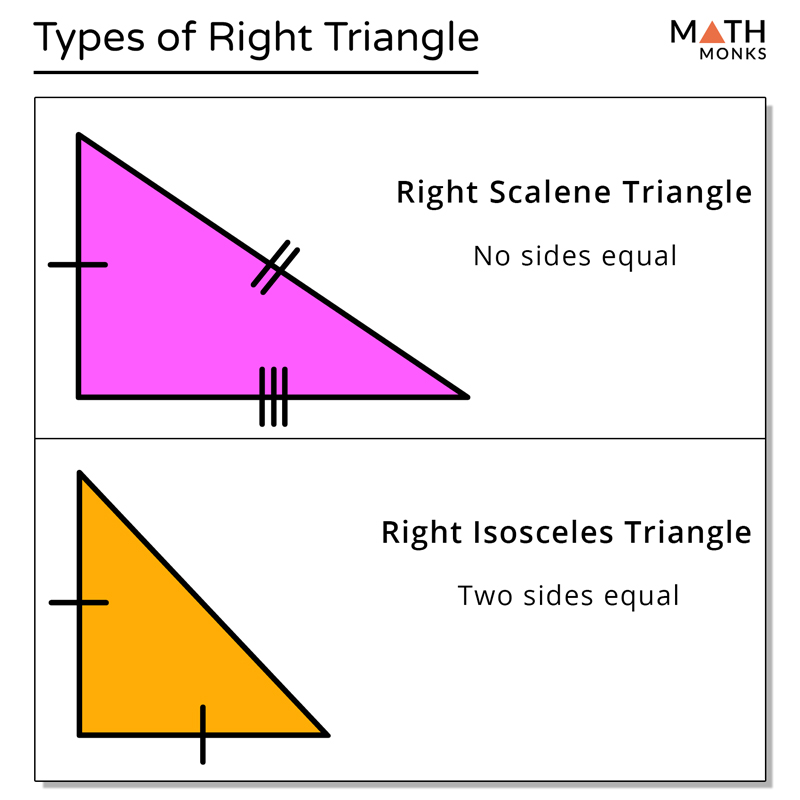
A right triangle can be scalene (having all three sides of different length) or isosceles (having exactly two sides of equal length). It can never be an equilateral triangle. In this article, you are going to study the definition, area, and perimeter of an isosceles right triangle in detail. Also, read:
What is the difference between a right triangle and an isosceles triangle?
An Isosceles triangle is a triangle with at lest two sides of the same length. A right triangle is a triangle with one right angle. It is possible to have an Isosceles-Right Triangle.
How to make a right triangle with two sides?
Here is how to answer this question yourself. Take two sticks, pencils, toothpicks of equal length. Then just place the pencils to make a square corner or right angle. Of course that is possible and easy to do. Then just join the other ends of the pencils to make the isosceles right triangle. Now you can see that this is always possible. In fact, it's the two adjacent sides of a square and the third side is a diagonal of the square. In fact, you can make a right triangle with two sides of ANY length. The length of third side or hypotenuse will always be the SQUARE ROOT OF THE SUM OF THE SQUARE
What is the isosceles triangle?
An isosceles triangle is a triangle that has 2 equal sides. A right triangle as a triangle with one angle being . I don’t know if you the converse of the isosceles triangle theorem [ 1] , which states that if the two angles of a triangle are congruent, then the sides opposite those angles are congruent. From the theorem, it is possible ...
How to draw a triangle?
_ (It does not matter if it looks like the sides are equal or not.) 2) Label the squarest of the angles of the triangle as being 90 degrees. _ (This is the right angle that makes your triangle a right triangle.) 3) How many degrees must the oth. Continue Reading.
What is the angle of a right angled triangle?
A right angled triangle is one with an angle 90 degrees. The other two angles of this triangle can be equal or not. But if the other two angles of a right angled triangle are equal (means 45 degrees each), then this triangle is isosceles, in addition to being right angled. In other words, it is an isosceles right angled triangle.
How to make isosceles right triangle?
Here is how to answer this question yourself. Take two sticks, pencils, toothpicks of equal length. Then just place the pencils to make a square corner or right angle. Of course that is possible and easy to do. Then just join the other ends of the pencils to make the isosceles right triangle.
How many sides does a right isosceles triangle have?
A right isosceles triangle has two equal sides, one on each side of and intersection at the 90 degree angle.
Isosceles Right Triangle Properties
Isosceles right triangle follows almost similar properties to an isosceles triangle. Let's look into the list of properties followed by the isosceles right triangle.
Isosceles Right Triangle Formula
Isosceles right triangle follows the Pythagoras theorem to give the relationship between the hypotenuse and the equal sides. Let's look into the diagram below to understand the isosceles right triangle formula.
Isosceles Right Triangle Examples
Example 1: The equal sides of a right isosceles triangle measures 8 units each. Find the area.
FAQs on Isosceles Right Triangle
An isosceles right triangle is defined as a triangle with two equal sides known as the legs, a right angle, and two acute angles which are congruent to each other.
What is the angle of an equilateral triangle called?
The angle included by the legs is called the vertex angle and the angles that have the base as one of their sides are called the base angles. The vertex opposite the base is called the apex. In the equilateral triangle case, since all sides are equal, any side can be called the base.
What is the difference between isosceles and equilateral triangles?
Terminology, classification, and examples. Euclid defined an isosceles triangle as a triangle with exactly two equal sides, but modern treatments prefer to define isosceles triangles as having at least two equal sides. The difference between these two definitions is that the modern version makes equilateral triangles (with three equal sides) ...
What are the sides of an isosceles triangle called?
The two equal sides are called the legs and the third side is called the base of the triangle. The other dimensions of the triangle, such as its height, area, and perimeter, can be calculated by simple formulas from the lengths of the legs and base. Every isosceles triangle has an axis of symmetry along the perpendicular bisector of its base. The two angles opposite the legs are equal and are always acute, so the classification of the triangle as acute, right, or obtuse depends only on the angle between its two legs.
How to tell if isosceles triangle is acute?
Whether an isosceles triangle is acute, right or obtuse depends only on the angle at its apex. In Euclidean geometry, the base angles can not be obtuse (greater than 90°) or right (equal to 90°) because their measures would sum to at least 180°, the total of all angles in any Euclidean triangle. Since a triangle is obtuse or right if and only if one of its angles is obtuse or right, respectively, an isosceles triangle is obtuse, right or acute if and only if its apex angle is respectively obtuse, right or acute. In Edwin Abbott 's book Flatland, this classification of shapes was used as a satire of social hierarchy: isosceles triangles represented the working class, with acute isosceles triangles higher in the hierarchy than right or obtuse isosceles triangles.
What is an isosceles triangle?
For other uses, see Isosceles (disambiguation). In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case .
How to partition an acute triangle?
Generalizing the partition of an acute triangle, any cyclic polygon that contains the center of its circumscribed circle can be partitioned into isosceles triangles by the radii of this circle through its vertices. The fact that all radii of a circle have equal length implies that all of these triangles are isosceles. This partition can be used to derive a formula for the area of the polygon as a function of its side lengths, even for cyclic polygons that do not contain their circumcenters. This formula generalizes Heron's formula for triangles and Brahmagupta's formula for cyclic quadrilaterals.
How many isosceles does a rhombus have?
Either diagonal of a rhombus divides it into two congruent isosceles triangles. Similarly, one of the two diagonals of a kite divides it into two isosceles triangles, which are not congruent except when the kite is a rhombus.
What are the equal sides of an isosceles triangle called?
The equal sides of an isosceles triangle are known as the ‘legs. ’
What is an isosceles triangle?
What is Isosceles Triangle? A triangle with two sides of equal length is an isosceles triangle. The two equal sides of an isosceles triangle are known as ‘legs’ whereas the third or unequal side is known as the ‘base’. Angles opposite to equal sides in an isosceles triangle are always of equal measure. In the given isosceles triangle, ...
Which angles are always equal?
The angles situated opposite to the equal sides of an isosceles triangle are always equal.
Which ancient civilizations knew how to calculate area?
Moreover, ancient Babylonian and Egyptian mathematics knew how to calculate ‘area’ long before the ancient Greek mathematicians studied the isosceles triangle. The isosceles shape of the buildings not only makes them attractive but also earthquake-resistant.
What is the measure of the vertex angle of a triangle?
Triangle XYZ is isosceles. The measure of the vertex angle, Y, is twice the measure of a base angle.
How many centimeters are in an isosceles triangle?
Isosceles triangle ABC has a perimeter of 96 centimeters. The base of the triangle is and measures 24 centimeters.
Which bisector creates two smaller isosceles triangles?
The perpendicular bisector of creates two smaller isosceles triangles.
What is the angle of M?
Angle M has a measure of 47°.
How many angles are congruent?
At least two of the angles are congruent.
Isosceles Triangle Shape
A = angle A a = side a B = angle B b = side b C = angle C c = side c A = C a = c h a = h c K = area P = perimeter See Diagram Below: h a = altitude of a h b = altitude of b h c = altitude of c
Calculator Use
An isosceles triangle is a special case of a triangle where 2 sides, a and c, are equal and 2 angles, A and C, are equal.
Overview
In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of
Terminology, classification, and examples
Euclid defined an isosceles triangle as a triangle with exactly two equal sides, but modern treatments prefer to define isosceles triangles as having at least two equal sides. The difference between these two definitions is that the modern version makes equilateral triangles (with three equal sides) a special case of isosceles triangles. A triangle that is not isosceles (having three unequ…
Formulas
For any isosceles triangle, the following six line segments coincide:
• the altitude, a line segment from the apex perpendicular to the base,
• the angle bisector from the apex to the base,
• the median from the apex to the midpoint of the base,
Isosceles subdivision of other shapes
For any integer , any triangle can be partitioned into isosceles triangles. In a right triangle, the median from the hypotenuse (that is, the line segment from the midpoint of the hypotenuse to the right-angled vertex) divides the right triangle into two isosceles triangles. This is because the midpoint of the hypotenuse is the center of the circumcircle of the right triangle, and each of the two triangles …
Applications
Isosceles triangles commonly appear in architecture as the shapes of gables and pediments. In ancient Greek architecture and its later imitations, the obtuse isosceles triangle was used; in Gothic architecture this was replaced by the acute isosceles triangle.
In the architecture of the Middle Ages, another isosceles triangle shape becam…
History and fallacies
Long before isosceles triangles were studied by the ancient Greek mathematicians, the practitioners of Ancient Egyptian mathematics and Babylonian mathematics knew how to calculate their area. Problems of this type are included in the Moscow Mathematical Papyrus and Rhind Mathematical Papyrus.
The theorem that the base angles of an isosceles triangle are equal appears as Proposition I.5 i…
Notes
1. ^ Heath (1956), p. 187, Definition 20.
2. ^ Stahl (2003), p. 37.
3. ^ Usiskin & Griffin (2008), p. 4.
4. ^ Usiskin & Griffin (2008), p. 41.
External links
• Weisstein, Eric W., "Isosceles triangle", MathWorld