So, for every x, identity function f(x) is differentiable. (ii) Given, constant function f(x) = c, where c is constant. Domain of function f(x) is set of real numbers (R). Let a be any arbitrary real number, then At x = a, Left hand derivative of f (x) So, for every x, identity function f(x) is differentiable.
Is identity function continuous?
Properties of Identity Function In topological space, this function is always continuous.
What is the derivative of identity function?
Let IX:X→X be the identity function. Then: I′X(x)=1. where I′X(x) denotes the derivative of IX with respect to x.
Which functions are differentiable?
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its domain.
How do you know if it is differentiable or not?
How to Prove a Function is Differentiable? A function can be proved differentiable if its left-hand limit is equal to the right-hand limit and the derivative exists at each interior point of the domain.
Why identity function is a real valued function?
An identity function is a real-valued function of the form g: R→R such that g(x) = x for any x ∈ R. R denotes the domain of the function g, which is a set of real numbers. Identity functions have the same domain and range. If the input is 5, the output will be 5 as well; if the input is 0, the output will be 0.
Why is it called identity function?
It is called an identity function because the image of an element in the domain is identical to the output in the range. Thus, an identity function maps each real number to itself. The output of an identity function is the same as its input.
What functions Cannot be differentiable?
A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at x = 0. Generally the most common forms of non-differentiable behavior involve a function going to infinity at x, or having a jump or cusp at x.
What functions are not differentiable?
A function is non-differentiable when there is a cusp or a corner point in its graph. For example consider the function f(x)=|x| , it has a cusp at x=0 hence it is not differentiable at x=0 .
What are the 2 conditions for differentiability?
Hence, differentiability is when the slope of the tangent line equals the limit of the function at a given point. This directly suggests that for a function to be differentiable, it must be continuous, and its derivative must be continuous as well.
Which equations are not differentiable?
A function is not differentiable at a if its graph has a vertical tangent line at a. The tangent line to the curve becomes steeper as x approaches a until it becomes a vertical line. Since the slope of a vertical line is undefined, the function is not differentiable in this case.
What function is continuous but not differentiable?
In mathematics, the Weierstrass function is an example of a real-valued function that is continuous everywhere but differentiable nowhere. It is an example of a fractal curve. It is named after its discoverer Karl Weierstrass.
How do you know if a function is differentiable but not continuous?
Relationship between Continuity and Differentiability: If a function is differentiable at a point, then it is continuous at that point. However if a function is continuous at a point, it is possible for it to not be differentiable.
What is the derivative of the identity matrix?
The identity function is given by F ( X ) = X . One would expect that the derivative of this function is the identity matrix, and of course we have D F ( X ) = I n q .
What is derivative of implicit function?
To differentiate an implicit function, we consider y as a function of x and then we use the chain rule to differentiate any term consisting of y. Now to differentiate the given function, we differentiate directly w.r.t. x the entire function. This step basically indicates the use of chain rule.
How do you derive identity matrix?
Identity MatricesA square matrix, I is an identity matrix if the product of I and any square matrix A is A. ... If the product of two square matrices, P and Q, is the identity matrix then Q is an inverse matrix of P and P is the inverse matrix of Q. ... AA-1 = A-1A = I.Since B is an inverse of A, we know that AB = I.
How do you find the derivative of a trigonometric identities?
2:164:49Finding the Derivative of Trig Functions - Derivatives CalculusYouTubeStart of suggested clipEnd of suggested clipAnd now we're going to multiply that by the first term sine of x. And now we can simplify this toMoreAnd now we're going to multiply that by the first term sine of x. And now we can simplify this to cosine squared x minus sine squared x. And this is actually a trig identity.
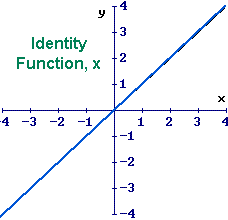
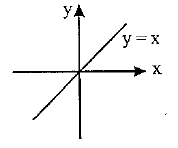
What is the slope of the identity function graph?
The slope of the identity function graph always remains as 1.
What is an identity function?
The identity function is an example of a polynomial function. It is a special type of linear function in which the output is the same as the input. The identity function is also known as an identity map or identity relation.
What is domain value?
The domain values are equal to the range values for an identity function. In this lesson, we will learn more about the identity function, its domain, range, graph, and properties with the help of examples.
When is a function considered an identity function?
A function is considered to be an identity function when it returns the same value as the output that was used as its input. That is, if g is an identity function, then the equality g (x) = x holds for all x.
Is the graph of an identity function and its inverse the same?
The graph of an identity function and its inverse are the same.
Is a function a constant?
A function is considered to be a constant function if it always returns the same constant value for every input value. For example g (x) =1 is a constant value as its output remains the same irrespective of what the input is. A function is considered to be an identity function when it returns the same output as the input. That is, if g is an identity function, then the equality g (x) = x holds for all x.
Is the co-domain and the range of an identity function equal sets?
The co-domain and the range of an identity function are equal sets. ⇒ The identity function is onto.
What is the difference between a differentiable function and a continuous function?
Hence the main difference between a differentiable and continuous function is that a differentiable function is always a continuous function but a continuous function may not be differentiable.
Why is the absolute value function not differentiable at 0?
The absolute value function is not differentiable at 0 because the graph of the function has a sharp corner at this point.
How to prove a function is differentiable?
A function can be proved differentiable if its left-hand limit is equal to the right-hand limit and the derivative exists at each interior point of the domain.
What is differentiation in calculus?
In calculus, differentiation of differentiable functions is a mathematical process of determining the rate of change of the functions with respect to the variable. Some common differentiability formulas that we use to solve various mathematical problems are:
Is a graph of a differentiable function continuous?
If a function is differentiable, then it is continuous. If a function is continuous, then it is not necessarily differentiable. The graph of a differentiable function does not have breaks, corners, or cusps.
Is a function always continuous?
We say that a function is continuous at a point if its graph is unbroken at that point. A differentiable function is always a continuous function but a continuous function is not necessarily differentiable.
When a function is differentiable, is it continuous?
If a function is differentiable, then it is continuous.
Why Bother?
Because when a function is differentiable we can use all the power of calculus when working with it.
Is floor and ceiling differentiable?
The Floor and Ceiling Functions are not differentiable at integer values, as there is a discontinuity at each jump. But they are differentiable elsewhere. At x=0 the derivative is undefined, so x (1/3) is not differentiable.
Can a function be continuous but not differentiable?
But a function can be continuous but not differentiable. For example the absolute value function is actually continuous (though not differentiable) at x=0.
Is x2 + 6x differentiable?
Derivative rules tell us the derivative of x 2 is 2x and the derivative of x is 1, so: Its derivative is 2x + 6. So yes! x 2 + 6x is differentiable. ... and it must exist for every value in the function's domain.
Does the limit exist at x=0?
The limits are different on either side, so the limit does not exist at x=0