What are all the irrational numbers?
The famous irrational numbers consist of Pi, Euler’s number, Golden ratio. Many square roots and cube roots numbers are also irrational, but not all of them. For example, √3 is an irrational number but √4 is a rational number. Because 4 is a perfect square, such as 4 = 2 x 2 and √4 = 2, which is a rational number.
Is 6 an irrational number?
Thus, the value obtained for the root of 6 satisfies the condition of being a non-terminating and non-repeating decimal number that keeps extending further after the decimal point which makes √6 an irrational number . Hence, √6 is an irrational number. Root 6 is most commonly used to term square root of 6.
What are some examples of irrational numbers?
What are some real life examples of irrational numbers?
- Pi, which begins with 3.14, is one of the most common irrational numbers.
- e, also known as Euler’s number, is another common irrational number.
- The Square Root of 2, written as √2, is also an irrational number.
Are irrational numbers real numbers?
Irrational numbers are the real numbers that cannot be represented as a simple fraction. It cannot be expressed in the form of a ratio, such as p/q, where p and q are integers, q≠0. It is a contradiction of rational numbers.
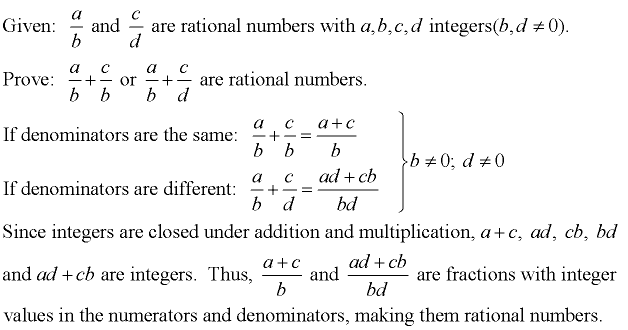
Why is the sum of a rational number and an irrational number is irrational?
Each time they assume the sum is rational; however, upon rearranging the terms of their equation, they get a contradiction (that an irrational number is equal to a rational number). Since the assumption that the sum of a rational and irrational number is rational leads to a contradiction, the sum must be irrational.
Is the sum of a rational and an irrational irrational examples?
Examples of Addition 4 + √3 is Irrational, as 4 is rational and √3 is irrational. 6 – √2 is Irrational, as 6 is rational and √2 is irrational. π – 2 is Irrational, as π is irrational and 2 is rational. √7 – 8 is Irrational, as √7 is irrational and 8 is rational.
Why is the sum of two rational numbers always rational?
"The sum of two rational numbers is rational." So, adding two rationals is the same as adding two such fractions, which will result in another fraction of this same form since integers are closed under addition and multiplication. Thus, adding two rational numbers produces another rational number.
What are the rules for rational and irrational numbers?
Properties of Rational and Irrational Numbers1: The sum of two rational numbers is also rational.2: The product of two rational numbers is rational.3: The sum of two irrational numbers is not always irrational.4: The product of two irrational numbers is not always irrational.
Is the sum of two irrational numbers always irrational example?
Sum of two irrational numbers is always irrational.
Is 0.575 a rational?
0.575 0.575 is rational. 5 5 is irrational.
Is the product of a rational number and an irrational number is irrational?
The product of any rational number and any irrational number will always be an irrational number.
Is the product of two irrational numbers always irrational example?
The product of two irrational numbers can be rational or irrational depending on the two numbers. For example, √3×√3 is 3 which is a rational number whereas √2×√4 is √8 which is an irrational number. As √3,√2,√4 are irrational. Hence, option D is correct.
Rational and Irrational Numbers
A rational number is any number that can be expressed as the fraction a/b, where a and b are integers. The set of rational numbers includes all whole numbers, proper and improper fractions (assuming the numerator and denominator are integers), terminating decimals, and repeating decimals. The following are examples of rational numbers:
What is the Sum of a Rational and Irrational Number?
The sum of a rational number and an irrational number will always be an irrational number. Proving this requires the use of an indirect proof. Using an indirect proof means to assume the opposite of what is being proven is true, and then find a contradiction that proves it is not true. Working through the proof will clarify this statement.
What is the sum/difference of rational numbers with the same denominator?
Now the sum/difference of rational numbers with the same denominator is simple the sum or difference of the numerators (thanks to the distributive proerty). Now if the denominato
What are integers closed under?
Now integers are also closed under addition, subtraction and multiplication.
Is the sum of a rational number and an irrational number always irrational?
The sum of a rational number and an irrational number is always irrational.
Can irrational numbers be even?
No it cannot. A (very) simple way to understand is to think that the irrational number is an odd number and the rational number is the even number. Adding them together will form an odd number, however large the numbers. Therefore, the same logic can be applied here.
Is x irrational in equation 3?
So from the above simple chain x in equation 3 must be a rational (it is the ratio of two integers) , so x cannot be irrational - regardless of what we claimed in statement a.
Is rational number a field?
The rational numbers are a field, so they are closed under addition of a finite number of elements:
Is sum and difference closed?
No. Sum and differences are closed over rational numbers, meaning the sum or difference of two rational numbers is always rational.
