
4.1: Extreme Values of Functions
- Absolute Extrema. Consider the function over the interval . ...
- Local Extrema and Critical Points. Consider the function shown in Figure . ...
- Locating Absolute Extrema. The extreme value theorem states that a continuous function over a closed, bounded interval has an absolute maximum and an absolute minimum.
Full Answer
How do you find the extreme value of a function?
4.1: Extreme Values of Functions Absolute Extrema. Consider the function over the interval . As .FN Therefore, the function does not have a largest value. Local Extrema and Critical Points. Consider the function shown in Figure . The graph can …
What are the extreme values of this function?
Finding Extreme Values In Exercises 53–68, find the extreme values (absolute and local) of the function and where they occur. 53. 54. 55. 56. 57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. Local Extrema and Critical Points In Exercises 69–76, find the critical points, domain endpoints, and ex-treme values (absolute and local) for each function. 69. 70. 71. 72. 73. 74.
How do you find extreme values?
The extreme values can be summarized as follows: f has a local and absolute minimum of 0 at 0. The value of f at x = -2 is approximately 1.587 and the value at x = 4 is approximately 2.520. Each is a local maximum... The absolute maximum value of f is approximately 2.520 at x = 4.
How to find extreme value?
An extreme value of a function is the largest or smallest value of the function in some interval. It can either be a maximum value, or a minimum value. We usually distinguish between local and global (or absolute) extreme values.
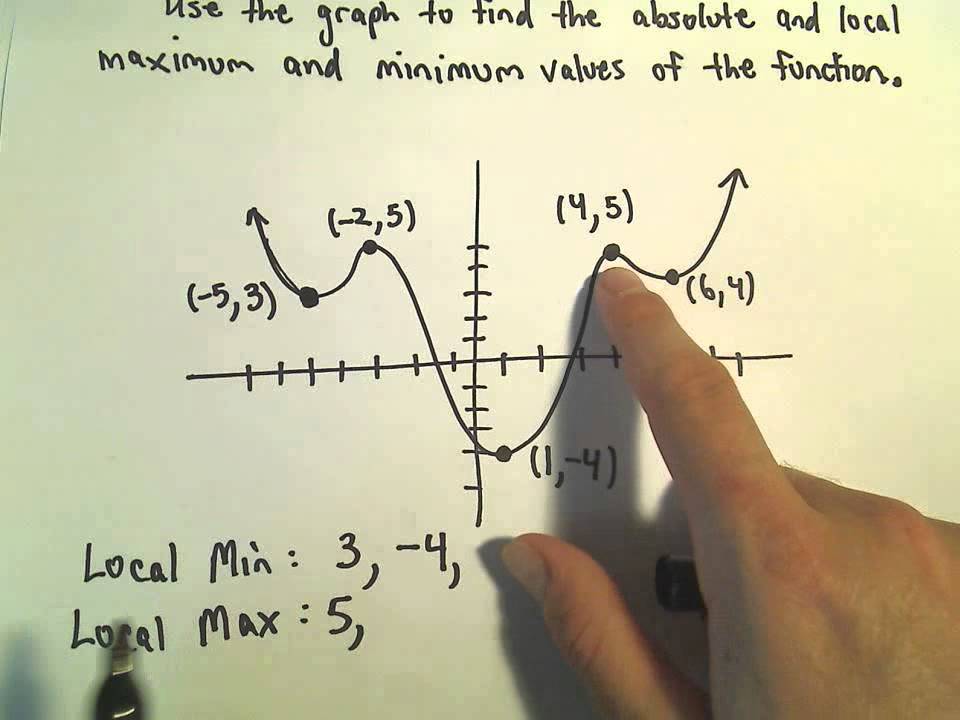
What are extreme values in a function?
The Extreme value theorem states that if a function is continuous on a closed interval [a,b], then the function must have a maximum and a minimum on the interval.
How do you find the extreme value of a function?
Explanation: To find extreme values of a function f , set f'(x)=0 and solve. This gives you the x-coordinates of the extreme values/ local maxs and mins. For example.Jul 5, 2018
What types of extreme values can a function have?
A function may have both an absolute maximum and an absolute minimum, have just one absolute extremum, or have no absolute maximum or absolute minimum. If a function has a local extremum, the point at which it occurs must be a critical point. However, a function need not have a local extremum at a critical point.Apr 27, 2019
What is meant by extreme values of a function of n variables?
An extreme value of f(x) subject to the condition g(x) = 0, is called a constrained extreme value and g(x)=0 is called the constraint. Definition 2.2. If f : Rn → R is a function of n variables, the Lagrangian function. of f subject to the constraint g(x1,...,xn) = 0 is the function of n + 1 variables.
How do you find extreme?
0:026:17Find the Extreme Value and Where it Occurs (Rational Function) - YouTubeYouTubeStart of suggested clipEnd of suggested clipRight now negative 1 I get negative 2x squared minus 1 subtract 1 from the power I get negative 2MoreRight now negative 1 I get negative 2x squared minus 1 subtract 1 from the power I get negative 2 but don't forget to multiply by the derivative of the inside and drew to the inside is going to be 2x.
Where do extreme values occur?
Since an absolute maximum must occur at a critical point or an endpoint, and x = 0 is the only such point, there cannot be an absolute maximum. A function's extreme points must occur at critical points or endpoints, however not every critical point or endpoint is an extreme point.
What are extreme values in a data set?
Extreme values (otherwise known as 'outliers') are data points that are sparsely distributed in the tails of a univariate or a multivariate distribution.
What is extreme values in statistics?
An extreme value is either very small or very large values in a probability distribution. These extreme values are found in the tails of a probability distribution (i.e. the distribution's extremities).Jan 8, 2022
What is the extreme value of a quadratic function?
The extreme value is the maximum or minimum value of a quadratic function.May 14, 2016
How do you find the extreme points of a function with two variables?
To find extrema of functions of two variables, first find the critical points, then calculate the discriminant and apply the second derivative test.Apr 27, 2019
How do you find the extreme value of a two variable function?
Two variable local extrema examplesFind the local extrema of f(x,y)=x3+x2y−y2−4y.The second solution for case 2 is when x=−4, which means y=−3x/2=6. Therefore, the point (−4,6) is a critical point.You should double check that Df(x,y)=[00] at each of these points.Identify the local extrama of f(x,y)=(x2+y2)e−y.
What is extreme point math?
An extreme point, in mathematics, is a point in a convex set which does not lie in any open line segment joining two points in the set. Extreme point or extremal point may also refer to: A point where some function attains its extremum.
What are the local extreme values of a function?
One of the most useful results of calculus is that the absolute extreme values of a function must come from a list of local extreme values , and those values are easily found using the first derivative of the function.
Why is the theorem important?
The theorem is important because it can guide our investigations when we search for absolute extreme values of a function. Theorem 1 If f is continuous on a closed interval [ a, b ], then f has both an absolute maximum value and an absolute minimum value on the interval. This theorem says that a continuous function that is defined on ...
Why is optimization important in differential calculus?
Optimization problems are one of the most important applications of differential calculus because we often want to know when the output of a function is at its maximum or minimum.
What is the extreme value theorem?
The extreme value theorem states that a function that is continuous over a closed interval is guaranteed to have a maximum or minimum value over a closed interval. The same cannot be said for functions that do not satisfy these conditions, although it is possible to find or construct such functions that have a maximum and minimum ...
Why don't continuous functions reach min/max?
There exist continuous functions on open intervals that don't reach min/max values, because they are unbounded in the interval (read: they can tend to -∞, ∞, or both on this open interval). If you are dealing with continuous functions on a closed interval, on the other hand, you know they reach max/minimums.
Does the Extreme Value Theorem require a closed interval?
No . The Extreme value theorem requires a closed interval. You cannot have a closed bound of ±∞ because ∞ is never a value that can actually be reached. Thus, a bound of infinity must be an open bound. So, it is (−∞, +∞), it cannot be [−∞, +∞].
Can you find the slope of a graph?
However, you can't find the slope if the graph is shaped funny, like a heart or a star, or happens to have a jump in it, like a set of steps. The heart and star may be continuous, but they are not differentiable, because they have a pointy edge at which you cannot calculate the slope.
Is graph continuous?
The fact that a graph is continuous makes a big difference when doing calculus. Let's say you had the function x^2. A, you know that function is something you can draw without lifting your pen, and b, you know that function's smooth and doesn't have any kinks or pointy edges in it.
