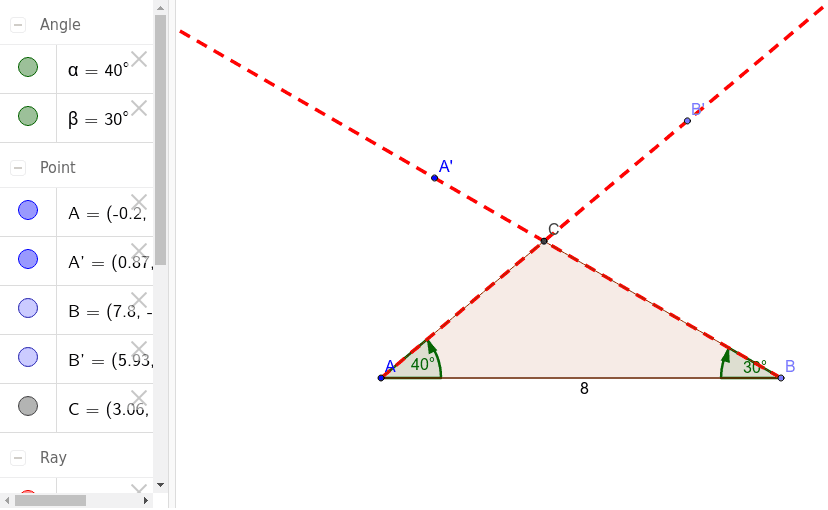
What is the difference between Asa and AAS?
The difference between ASA and AAS is that ASA refers to the angle opposite the side where the angle is adjacent to, while AAS refers to the angle opposite the side where it is acute. Both are used in geometry and trigonometry, but their meanings are different.
What are the differences of Asa congruence and SAS?
SAS (side-angle-side) Two sides and the angle between them are congruent. ASA (angle-side-angle) How do you use ASA in geometry? "ASA" is when we know two angles and a side between the angles. then use The Law of Sines to find each of the other two sides. Example 1. angle A = 76° angle B = 34° and c = 9.
How to solve Asa?
Solving ASA Triangles "ASA" means "Angle, Side, Angle" "ASA" is when we know two angles and a side between the angles. To solve an ASA Triangle. find the third angle using the three angles add to 180 ...
What is SSS, SAS, ASA, AAS in geometry?
What is SSS, AAS, SAS, and ASA?
- SSS refers to the equality of three sides between triangles.
- AAS refers to the equality between two sides and an angle between triangles.
- SAS refers to the equality between two sides and an angle (between the sides) between triangles.
- ASA refers to the equality between two angles and one side between triangles.
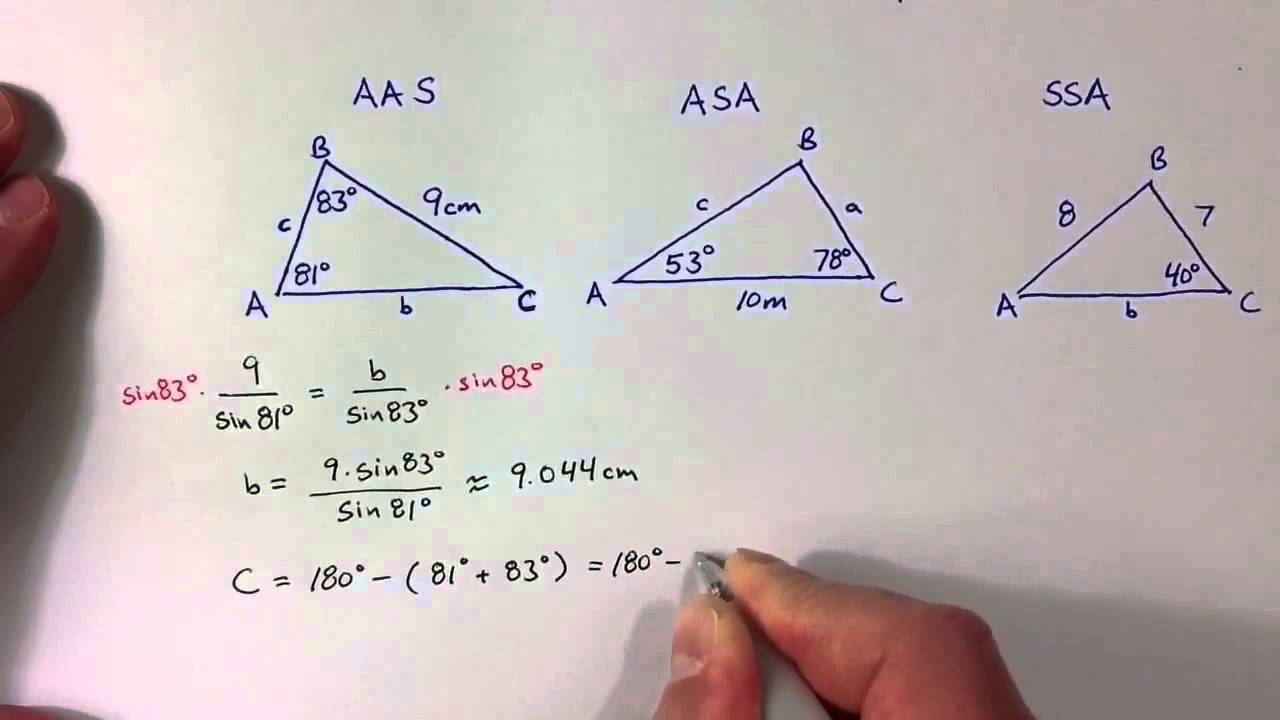
What does ASA in geometry mean?
Angle-Side- AngleASA (Angle-Side- Angle) If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.
What is ASA SAS SSS in geometry?
SAS stands for “side, angle, side” and means that we have two triangles where we know two sides and the included angle are equal. If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent. ASA (angle, side, angle)
What does AAS and ASA mean?
If two pairs of corresponding angles and the side between them are known to be congruent, the triangles are congruent. This shortcut is known as angle-side-angle (ASA). Another shortcut is angle-angle-side (AAS), where two pairs of angles and the non-included side are known to be congruent.
Is Asa same as AAS?
ASA stands for "angle, side, angle" and means that we have two triangles where we know two angles and the included side are equal. And AAS stands for "angle, angle, side" and means that we have two triangles where we know two angles and the non-included side are equal.
What is SSS SAS ASA AAS and HL?
SSS, or Side Side Side. SAS, or Side Angle Side. ASA, or Angle Side Side. AAS, or Angle Angle Side. HL, or Hypotenuse Leg, for right triangles only.
Is AAS same as SAA?
– ASA and AAS are two postulates that help us determine if two triangles are congruent. ASA stands for “Angle, Side, Angle”, while AAS means “Angle, Angle, Side”. Two figures are congruent if they are of the same shape and size. In other words, two congruent figures are one and the same figure, in two different places.
Are AAA triangles congruent?
Knowing only angle-angle-angle (AAA) does not work because it can produce similar but not congruent triangles. When you're trying to determine if two triangles are congruent, there are 4 shortcuts that will work. Because there are 6 corresponding parts 3 angles and 3 sides, you don't need to know all of them.
What is SSA in math?
SSA stands for side side angle postulate. In this postulate of congruence, we say that if two sides and an angle not included between them are respectively equal to two sides and an angle of the other triangle then the two triangles are equal.
What is the difference between ASA and AAS congruence rule?
Accoriding to ASA congruence rule when two angles and included side of one triangle is equal to two angles and included side of another side they the two triangles are congruent. But according to AAS, two angles and one side of a triangle are equal to two angles and one side of another triangle then they are congruent.
How do I know my SSS SAS ASA AAS?
1:068:40Triangle Congruence - SSS, SAS, ASA and AAS 128-2.16 - YouTubeYouTubeStart of suggested clipEnd of suggested clipIf we've got that situation where we've got three pairs of congruent sides then those two trianglesMoreIf we've got that situation where we've got three pairs of congruent sides then those two triangles are going to be congruent. So this is called side-side-side congruency.
What are the 5 congruence theorems?
Thus the five theorems of congruent triangles are SSS, SAS, AAS, HL, and ASA.SSS – side, side, and side. ... SAS – side, angle, and side. ... ASA – angle, side, and angle. ... AAS – angle, angle, and side. ... HL – hypotenuse and leg.
How do I know my SSS SAS ASA AAS?
1:068:40Triangle Congruence - SSS, SAS, ASA and AAS 128-2.16 - YouTubeYouTubeStart of suggested clipEnd of suggested clipIf we've got that situation where we've got three pairs of congruent sides then those two trianglesMoreIf we've got that situation where we've got three pairs of congruent sides then those two triangles are going to be congruent. So this is called side-side-side congruency.
What is the ASA formula?
ASA formula is one of the criteria used to determine congruence. ASA congruence criterion states that, "if two angles of one triangle, and the side contained between these two angles, are respectively equal to two angles of another triangle and the side contained between them, then the two triangles will be congruent".
What is AAS and SSA?
AAS - angle angle side. SSA - side side angle.
What is the difference between ASA and AAS?
ASA and AAS are two postulates that determine if two triangles are congruent. ASA stands for “Angle, Side, Angle”, that is, any two angles and the included side while AAS means “Angle, Angle, Side”, that is, the two corresponding angles and the non-included side
What is ASA Congruence Rule?
Under this rule, two triangles are said to be congruent if any two angles and the side included between them of one triangle are equal to the corresponding angles and the included side of the other triangle. Look at the image given below to determine if the two given triangles, Δ ABC and ΔXYZ are congruent by the ASA rule.
How to tell if two triangles are congruent?
We can identify if the two triangles are congruent by checking if the parts of one triangle are equal to the corresponding parts of the other triangle. As the name says, ASA can be identified in case the two angles and the included side of one triangle are equal to two angles and included side of another triangle.
How many sides and angles are congruent?
Two triangles are said to be congruent if the six elements (three sides and three angles) of one triangle are equal to the corresponding six elements of the other triangle.
What is the congruence rule of ASA?
The statement of ASA congruence rule is given as: "If two angles and the included side of one triangle are equal to two angles and included side of another triangle, then the triangles are congruent".
What is the ASA criterion for a side BC?
Under ASA criterion, Δ ABC ≅ ΔXYZ, as ∠B = ∠Y, ∠C = ∠Z, and the side BC = YZ. Since Δ ABC ≅ ΔXYZ, then the third angle ∠A and the other two sides of Δ ABC are bound to be equal to the corresponding angle ∠X and the sides of ΔXYZ.
What is the symbol for congruence?
The congruency is expressed using the symbol (≅).
Why are the third angles of a triangle congruent?
Because the triangles are congruent, the third angles (R and N) are also equal . Because the triangles are congruent, the remaining two sides are equal (PR=LN, and QR=MN) . But don't forget: Congruent triangles can be rotated and/or mirror images of each other (reflected). (See Congruent triangles.)
What is congruent triangle?
Congruent Triangles - Two angles and included side (ASA)
What is the ASA theorem?
ASA Theorem (Angle-Side-Angle) The Angle Side Angle Postulate (ASA) says triangles are congruent if any two angles and their included side are equal in the triangles. An included side is the side between two angles.
Which postulate says triangles are congruent?
Perhaps the easiest of the three postulates, Side Side Side Postulate (SSS) says triangles are congruent if three sides of one triangle are congruent to the corresponding sides of the other triangle. This is the only postulate that does not deal with angles.
What is the congruence of triangles?
Triangle Congruence Theorems (SSS, SAS, & ASA Postulates) Triangles can be similar or congruent. Similar triangles will have congruent angles but sides of different lengths. Congruent triangles will have completely matching angles and sides. Their interior angles and sides will be congruent.
How do you know if two triangles are congruent?
Two triangles are congruent if their corresponding sides are equal in length and their corresponding interior angles are equal in measure.
What are the three parts of a triangle that must be congruent?
For the two triangles to be congruent, those three parts -- a side, included angle, and adjacent side -- must be congruent to the same three parts -- the corresponding side, angle and side -- on the other triangle, △ Y AK △ Y A K.
Is the line segment SW or NA congruent?
You also know that line segments SW and NA are congruent, because they were part of the parallelogram (opposite sides are parallel and congruent). So now you have a side SA, an included angle ∠WSA, and a side SW of △ SW A △ S W A. You can compare those three triangle parts to the corresponding parts of △ SAN △ S A N:
Can you cut up a textbook to check two triangles?
You could cut up your textbook with scissors to check two triangles. That is not very helpful, and it ruins your textbook. If you are working with an online textbook, you cannot even do that. Geometricians prefer more elegant ways to prove congruence.
