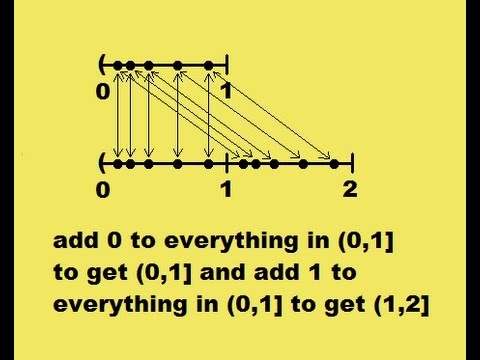
In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that a Cartesian
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular directed lines, measured in the same unit of length.
Full Answer
What is the axiom of choice in geometry?
The Axiom of Choice tells us that there is a set containing an element from each of the sets in the bag. Basically, this allows us to meaningfully extract elements from infinitely large collections of sets. In fact, it allows us to do this even if each set contains an infinite number of elements themselves!
What is the negation of the axiom of choice?
Axiom — For any set X of nonempty sets, there exists a choice function f that is defined on X and maps each set of X to an element of the set. Thus, the negation of the axiom of choice states that there exists a collection of nonempty sets that has no choice function. ( , so where is negation.)
What is an example of a weak axiom of choice?
There are several weaker statements that are not equivalent to the axiom of choice, but are closely related. One example is the axiom of dependent choice (DC). A still weaker example is the axiom of countable choice (AC ω or CC), which states that a choice function exists for any countable set of nonempty sets.
What is the proof requiring the axiom of choice?
A proof requiring the axiom of choice may establish the existence of an object without explicitly defining the object in the language of set theory.

What does the axiom of choice say?
The axiom of choice is an axiom in set theory with wide-reaching and sometimes counterintuitive consequences. It states that for any collection of sets, one can construct a new set containing an element from each set in the original collection. In other words, one can choose an element from each set in the collection.
What are axioms in simple terms?
In mathematics or logic, an axiom is an unprovable rule or first principle accepted as true because it is self-evident or particularly useful. “Nothing can both be and not be at the same time and in the same respect” is an example of an axiom.
What is axioms give example?
Axioms or Postulate is defined as a statement that is accepted as true and correct, called as a theorem in mathematics. Axioms present itself as self-evident on which you can base any arguments or inference. These are universally accepted and general truth. 0 is a natural number, is an example of axiom.
What is the problem with axiom of choice?
The axiom of choice has generated a large amount of controversy. While it guarantees that choice functions exist, it does not tell us how to construct those functions. All the other axioms that tell us that sets exist also tell us how to construct those sets. For example, the powerset operator is very well defined.
Does axiom mean truth?
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word ἀξίωμα (axíōma), meaning 'that which is thought worthy or fit' or 'that which commends itself as evident'.
What are the 3 axioms?
Axioms of Probability: Axiom 1: For any event A, P(A)≥0. Axiom 2: Probability of the sample space S is P(S)=1. Axiom 3: If A1,A2,A3,⋯ are disjoint events, then P(A1∪A2∪A3⋯)=P(A1)+P(A2)+P(A3)+⋯
Is axiom the same as truth?
Contents. In logic and mathematics, an axiom is not necessarily a self-evident truth, but rather a formal logical expression used in a deduction to yield further results.
Why do we use axioms?
Axioms are important to get right, because all of mathematics rests on them. If there are too few axioms, you can prove very little and mathematics would not be very interesting. If there are too many axioms, you can prove almost anything, and mathematics would also not be interesting.
What is the purpose of axioms?
Let look at this explanation: Any axiom is a statement that is so evident or well-established that it is accepted without controversy or question. It serves as a starting point from which other statements are logically derived.
What happens if you don't accept the axiom of choice?
If you remove the Axiom of Choice, then it is consistent that the real numbers can be written as a countable union of countable sets.
Who proved the axiom of choice?
1. Origins and Chronology of the Axiom of Choice. In 1904 Ernst Zermelo formulated the Axiom of Choice (abbreviated as AC throughout this article) in terms of what he called coverings (Zermelo 1904).
What is the axiom theory?
An axiomatic theory of truth is a deductive theory of truth as a primitive undefined predicate. Because of the liar and other paradoxes, the axioms and rules have to be chosen carefully in order to avoid inconsistency.
What is an axiom for kids?
An axiom is a concept in logic. It is a statement which is accepted without question, and which has no proof. The axiom is used as the premise or starting point for further reasoning or arguments, usually in logic or in mathematics.
What is another term of axiom?
Words related to axiom adage, aphorism, dictum, maxim, precept, proverb, theorem, apothegm, device, fundamental, law, moral, postulate, proposition, saying, truism, truth.
What is the purpose of axioms?
Let look at this explanation: Any axiom is a statement that is so evident or well-established that it is accepted without controversy or question. It serves as a starting point from which other statements are logically derived.
What does axiom mean in geometry?
An axiom, sometimes called postulate, is a mathematical statement that is regarded as “self-evident” and accepted without proof. It should be so simple that it is obviously and unquestionably true. Axioms form the foundation of mathematics and can be used to prove other, more complex results.
What axiom did Zermelo introduce?
1904/1908. Zermelo introduces axioms of set theory , explicitly formulates AC and uses it to prove the well-ordering theorem, thereby raising a storm of controversy. 1904. Russell recognizes AC as the multiplicative axiom: the product of arbitrary nonzero cardinal numbers is nonzero.
What is the original form of the axiom of choice?
Zermelo’ s original form of the Axiom of Choice, AC1, can be expressed as a scheme of sentences within a suitably strengthened version of (L). Accordingly we now suppose (L) to contain in addition predicate variables (X), (Y), (Z), … and second-order function variables (F), (G), (H), …. Here a second-order function variable (F) may be applied to a predicate variable (X) to yield an individual term (FX). The scheme of sentences
How did Fraenkel prove AC?
As stated above, in 1922 Fraenkel proved the independence of AC from a system of set theory containing “atoms”. Here by an atom is meant a pure individual, that is, an entity having no members and yet distinct from the empty set (so a fortiori an atom cannot be a set). In a system of set theory with atoms it is assumed that one is given an infinite set (A) of atoms. One can build a universe (V (A)) of sets over (A) by starting with (A), adding all the subsets of (A), adjoining all the subsets of the result, etc., and iterating transfinitely. (V (A)) is then a model of set theory with atoms. The kernel of Fraenkel’s method for proving the independence of AC is the observation that, since atoms cannot be set-theoretically distinguished, any permutation of the set (A) of atoms induces a structure-preserving permutation—an automorphism —of the universe (V (A)) of sets built from (A). This idea may be used to construct another model (Sym (V)) of set theory—a permutation or symmetric model —in which a set of mutually disjoint pairs of elements of (A) has no choice function.
What is choice function?
A choice function on A is thus a “choice” of an element of the variable set A at each stage; in other words, a choice function on A is a variable element of A. AC1 is then equivalent to the assertion. AC2: Any indexed collection of sets has a choice function.
What is the multiplicative axiom?
The Multiplicative Axiom (Russell 1906). The product of any set of non-zero cardinal numbers is non-zero.
What is AC2 in math?
Informally speaking, AC2 amounts to the assertion that a variable set with an element at each stage has a variable element.
Who created the axiom of choice?
Origins and Chronology of the Axiom of Choice. In 1904 Ernst Zermelo formulated the Axiom of Choice (abbreviated as AC throughout this article) in terms of what he called coverings (Zermelo 1904).
What is the axiom of choice?
The axiom of choice is an axiom in set theory with wide-reaching and sometimes counterintuitive consequences. It states that for any collection of sets, one can construct a new set containing an element from each set in the original collection. In other words, one can choose an element from each set in the collection.
Do mathematicians believe in the axiom of choice?
Nevertheless, there are mathematicians who either do not "believe in" the axiom of choice or who are interested in the logical repercussions of disallowing this a xiom in their set theory. For instance, some mathematicians identified as "constructivists" believe that mathematical objects only exist if they can be constructed explicitly, so the axiom of choice and its nonconstructive nature are unacceptable. The majority of (non-logician) mathematicians view acceptance of the axiom of choice at least partly as a matter of convenience; the theoretical tools that the axiom of choice makes available allow for a richer theory in many contexts where it applies. For instance, knowing that every vector space has a basis can be helpful for proofs and other constructions, even when no explicit basis can be constructed.
What is the point of the well-ordering theorem?
The point is that the necessary choice is given to us for free by the well-ordering theorem.
What is the upper bound of a chain?
X X which are all comparable to each other, an upper bound of a chain is an element that is comparable to and "greater than" all the elements of the chain, and a maximal element is an element. x ∈ X. xin X x ∈ X such that there is no.
Who introduced the axiom of choice?
The axiom of choice was initially introduced by Zermelo in order to prove the following theorem:
Is the well-ordering theorem equivalent to the axiom of choice?
It turns out that the well-ordering theorem is logically equivalent to the axiom of choice--that is, each one implies the other using only ZF set theory. Here is another equivalent statement that is often used in proofs:
Is the axiom of choice weaker than the axiom of choice?
There are quite a few statements which are weaker than the axiom of choice--the axiom of choice can be used to prove them, but the reverse implication is not true.
What does it do for us?
The hat puzzle is obviously a little contrived, but the axiom of choice has a lot of surprising and sometimes disconcerting implications that are relevant to other fields of math. Some of these consequences are apparent paradoxes; others are things we would very much like to be true, and make the axiom of choice extremely useful.
Why is the axiom of choice trivial?
One reason the axiom of choice can sound trivial is that there are a lot of superficially similar rules that are totally fine; the controversial bit is subtle. So here are a few things that don’t cause controversy:
Why do we choose axioms?
We choose axioms because they are USEFUL. Dealing with infinite quantities is weird and unintuitive (even without considering AC), but it is useful because it allows us to do things like approximate the physical world as continuous. The unsavory implications of AC all occur with truly infinite sizes so they never come up in practice. Therefore we should be comfortable accepting AC.
How to start a friendly fight in math?
One of the easiest ways to start a (friendly) fight in a group of mathematicians is to bring up the axiom of choice. This axiom has a really interesting place in the foundations of mathematics, and I wanted to see if I can explain what it means and why it’s controversial. As a bonus, we’ll get some insight into what an axiom is and how to think about them, and about how we use math to think about the actual world.
What is the axiom of choice?
Axiom of Choice: Given a collection of (non-empty) sets, we can choose one element from each set. 1
What is the philosophy of math that rejects the existence of infinite objects?
But we can also talk about Finitism, which is a philosophy of math that rejects the existence of infinite objects. (Or even ultrafinitism, which rejects the existence of large finite sets!)
What is the parallel postulate?
Parallel postulate: There is at most one line that can be drawn parallel to another given one through an external point.
What is the axiom of choice?
The theorem makes use of the Axiom of Choice (AC), which says that if you have a collection of sets then there is a way to select one element from each set. It has been proved that AC cannot be derived from the rest of set theory but must be introduced as an additional axiom. Since AC can be used to derive counterintuitive results such as the Banach-Tarski theorem, some mathematicians are very careful to specify when their arguments depend on AC.
What is the joke about the Banach Tarski theorem?
The joke is really about the Banach-Tarski theorem, which says that you can cut up a sphere into a finite number of pieces which when reassembled give you two spheres of the same size as the original sphere. This theorem is extremely counterintuitive since we seem to be doubling volume without adding any material or stretching the material that we have.
Why is the Banach-Tarski paradox counterintuitive?
The reason the Banach-Tarski paradox is counterintuitive is that we expect that if you split up a sphere into finitely many pieces, the total "mass" of all the pieces is still the same - so you shouldn't be able to put those pieces together again into something of twice the total "mass." The reason this reasoning doesn't apply is that the pieces in question don't have mass at all! This is not the same as saying that they have zero mass. It's something much more terrifying: the notion of "mass" (which to a mathematician generally means something precise called measure) can't be defined for these pieces (in a way that still preserves all the reasonable properties we want of our notion of mass).
What is existential instantiation?
This process, called existential instantiation, allows us to move from "the set is not empty" to "here is an element of the set". And this is, in effect, means that we [or rather the inference rule] chose some arbitrary element from S.
Is the Banach Tarski theorem right at the ZF axiom?
So, in the presence of the ZF axioms, there's really a range of axioms between the axiom of choice and nothing; somewhere in amongst that tumult is the Banach-Tarski theorem, and it is neither right at the top (read: equivalent to the axiom of choice) nor right at the bottom (read: equivalent to the empty condition.)
How many reputations do you need to answer a highly active question?
Highly active question. Earn 10 reputation (not counting the association bonus) in order to answer this question. The reputation requirement helps protect this question from spam and non-answer activity.
Can you use existential instantiation infinitely many times?
We cannot use existential instantiation infinitely many times . Remember that mathematics, formally, is always on its way to prove something. Proofs are finite in nature, so you can only apply the inference rule for finitely many of these S n 's.
Why (!!) the Axiom of Choice?
I start this section with a quote from an answer on MathOverflow, titled “ How I Learned to Stop Worrying and Love the Axiom of Choice”. See here.
Why is the axiom of choice important?
The short answer, not at all rigorous answer, is that the axiom of choice allows mathematicians to extract elements from an infinite number of infinitely large sets at once. This turns out to be very important, because mathematicians are very fond indeed of making infinite-sized things, and even more fond of being able to formalise their ...
How does the axiom of choice work?
The Axiom of Choice tells us that there is a set containing an element from each of the sets in the bag. Basically, this allows us to meaningfully extract elements from infinitely large collections of sets. In fact, it allows us to do this even if each set contains an infinite number of elements themselves! As those sets are often characterised by some property, the elements we get ‘chosen’ for us by the Axiom of Choice will often have structure we can exploit!
What would happen if there was no axiom of choice?
Without the Axiom of Choice, a lot of things fall apart, and rather quickly.
What does "more bags than sweets" mean?
What does this mean? It means that you can take a set, distribute all of its elements into different parts, and end up with more parts than you have elements. Imagine taking a set of different sweets, all of different colours, putting two in each bag, and ending up with more bags than sweets!
Is the axiom of choice consistent with the other axioms of set theory?
It has been proven that the Axiom of Choice is consistent with the other axioms of set theory, but so its negation. I.e. we don’t need to worry about it messing up our consistency with the apparatus we use for finite sets.
Do you need an axiom of choice?
dealing with finite numbers, finite graphs, a finite number of people, etc…), then you will never need the Axiom of Choice. That includes lots of interesting maths, from computer science to graph theory. And it probably includes everything in the real world.
Why is the axiom of determinacy contrary to the axiom of choice?
Another reason is that the axiom of choice results in things that are not constructive. It implies, among other things, that there is a well-ordering of the real numbers.
What is the supposed set of a set called?
The supposed set, often called the “choice set, ” has “chosen” an element from each of the nonempty disjoint sets. One thing that is important to note is that this is a non-constructive way to come up with a set. This axiom is assumed by most mathematicians today, but still encounters opposition by some.
Why is the axiom of choice controversial?
The Axiom of Choice is well known and controversial because some of its consequences, including (possibly) the well-ordering principle and (more likely) things like the Banach-Tarski paradox, leave some people uncomfortable that they could be “true”.
When did Zermelo propose the axiom of choice?
Mathematicians, at this point, were still uncertain on what exactly constituted a set. So in 1908 , Zermelo proposed the first set of axioms. However, there were some flaws with Zermelo’s axioms.
Is the axiom of countable sets true?
The axiom is uninterestingly true for finite sets, and for countable sets it is not particularly controversial. It is only counterintuitive and wrong for sets of size continuum or higher, that is for the set of all subsets of the integers (or larger) or, equivalently, the set of real numbers.
Who proposed the Zermelo-Fraenkel axioms?
In 1922, as a solution to these flaws, Abraham Fraenkel proposed other axioms which gave birth to the Zermelo-Fraenkel axioms, denoted by ZF. The Zermelo-Fraenkel axioms in addition to the Axiom of Choice is denoted as ZFC. Zermelo’s Axiom of Choice has many equivalent forms.

Easy Choices
What’s The Problem?
- The axiom of choice has weird effects precisely because it is so unlimited. It tells us that given any infinite collection of infinite sets, we can pick one option from each set, even if the sets are too big to really understand, and even if we don’t have any extra structure to guide us. We can see how this matters by looking at a classic logic puzzle, and then taking it to infinity. Imagine a gam…
What Does It Do For Us?
- The hat puzzle is obviously a little contrived, but the axiom of choice has a lot of surprising and sometimes disconcerting implications that are relevant to other fields of math. Some of these consequences are apparent paradoxes; others are things we would very much like to be true, and make the axiom of choice extremely useful. Zorn’s Lemma is probably the most common use of …
So…Is It True?
- The big question is: shouldwe believe any of these statements? That might be a surprising question. Isn’t the whole point of math to have definitive, objectively correct answers? Either we can prove a result is true, or we can’t. We don’t generally ask whether we feel like believing a theorem. We proved it; we’re stuck with it. But axiomsare a little different. We need to decide on …
Not as Crazy as It Seems
- This might feel like it’s dodging the question, though. If infinity is fake, why should we use axioms that only matter for infinity? And if we are going to say things about infinity, shouldn’t they make sense? Maybe it’s fine for a physicist to dismiss mathematical abstractions as unphysical and thus irrelevant. But math is about reasoning through the consequences of abstract hypothetical…
What’s The Point?
- The axiom of choice is logically independent of our axioms for set theory, so we can’t ever prove it true or false. And it says deeply strange things about deeply strange situations that can never really happen. So why does it matter? The answer is the same as the reason we use infinity at all. Everything we’ve ever seen is finite and discrete: objects are made out of atoms, and even if spa…
Just Relax
- If we’re trying to model the world, any infinite set we have to deal with will be a limit of finite sets. And any infinite family of infinite sets will be a limit of finite families of finite sets. And we know we have choice for finite sets of finite sets. So we can always get choice for these specific infinite sets, if we really need it—just by taking the limit of the elements we chose from our finite familie…