
Full Answer
How to solve problems using proportional reasoning?
set up proportions and use them to solve problems. write proportions as equations, in the form, y = kx, and use the equations to find other converted measurements. identify the constant of variation from different representations.
What is the definition of proportional in math?
What is a proportion in math definition? Proportion is an equation which defines that the two given ratios are equivalent to each other. In other words, the proportion states the equality of the two fractions or the ratios. When two ratios are equal in value, then they are said to be in proportion. What is proportion with example?
What is a non proportional equation?
If a relationship is nonlinear, it is non-proportional. If it is linear, it may be either proportional or non-proportional. When the graph of the linear relationship contains the origin, the relationship is proportional. Linear equations can be written in the form y = mx + b. When b ≠ 0, the relationship between x and y is non proportional.
What is approximate reasoning?
Approximate Reasoning is the process or processes by which a possible imprecise conclusion is deduced from a collection of imprecise premises. Fuzzy logic plays the major role in approximate reasoning. It has the ability to deal with different types of uncertainty.

What is the importance of proportional reasoning?
Proportional reasoning means that a student is flexible with numbers. When a student can break down numbers easily and see them in different ways, it helps the student solve problems with a variety of strategies and methods. Students need to have a toolkit of strategies to solve problems that they can quickly use.
How do you calculate proportional reasoning?
Proportional reasoning relies on ratios. A key idea is that every ratio can be written as a fraction, and every fraction can be thought of as a ratio. Example: I make just 2/3 as much as my husband – this is thinking about it as a fraction. Thinking about it as a ratio, I might say – I make $2 for every $3 he makes.
What is an example of a proportional relationship?
Now, we're going to consider an example of proportional relationship in our everyday life: When we put gas in our car, there is a relationship between the number of gallons of fuel that we put in the tank and the amount of money we will have to pay. In other words, the more gas we put in, the more money we'll pay.
What is proportional reasoning?
Proportional reasoning involves thinking about relationships and making comparisons of quantities or values. In the words of John Van de Walle, “Proportional reasoning is difficult to define. It is not something that you either can or cannot do but is developed over time through reasoning …
How do you use proportional reasoning to solve problems?
0:038:282.6 Math 7 - Apply Proportional Reasoning to Solve ProblemsYouTubeStart of suggested clipEnd of suggested clipBy 18. So that's why i put these extra boxes in here if i multiply by 18 i get 36. And here in orderMoreBy 18. So that's why i put these extra boxes in here if i multiply by 18 i get 36. And here in order to keep that ratio. Correct i'm going to multiply by 18. Here also when i multiply by 18.
How do you explain proportional relationships?
Proportional relationships are relationships between two variables where their ratios are equivalent. Another way to think about them is that, in a proportional relationship, one variable is always a constant value times the other. That constant is know as the "constant of proportionality".
What is a real life example of direct proportional?
For example, the weight of a person, the number of construction workers working, the number of bananas, the amount of dog food a dog eats, the distance between two towns or the speed of a horse at a full gallop.
What are the 3 kinds of proportion?
Types of ProportionsDirect Proportion.Inverse Proportion.
How does proportional reasoning solve real world problems?
We can use proportions to solve real-world problems by using the following steps: Use the information in the problem to set up two ratios comparing the same quantities. One of your ratios will contain the unknown. Set the ratios equal creating a proportion.
What is a proportional relationship 7th grade math?
A proportional relationship between two quantities is a collection of equivalent ratios, related to each other by a constant of proportionality. Proportional relationships can be represented in different, related ways, including a table, equation, graph, and written description.
What is an example of a relation in real life?
A person owns one dog, and the dog is owned by one person. In monogamous relationships, one person has one partner, who is only partnered with that person. One person owns one car, and the car is owned by one person. One child sleeps in one bed, and the bed is used by one child.
What is proportional thinking?
Proportional thinking is required in many activities of our daily lives, such as adjusting a cake recipe after realizing that one has only 200 g of flour instead of the required 300 g or splitting the cake among 12 people.
What is the importance of proportions in representation?
Although there is still an important aspect of representation involved, the focus on proportions also puts more weight on the mental operations that need to be performed on the representations, i.e., the mapping procedures. An example of this is the number line estimation task ( Siegler & Opfer, 2003 ). In this procedure, a number (e.g., 4) has to be placed on a line in a position that is determined by the values present at its extremities (for instance, toward the left of the midpoint if the extremes are 1 on the left and 9 on the right). This task has often been considered as directly revealing the underlying number representations. Specifically, the fact that children initially assign more space to the mapping of small numbers and compress larger numbers in the remaining space has been taken as evidence that mental number line representation develops from a nonlinear compressed representation to a linearized version. Contrary to this view, Newcombe et al. emphasize that the number line task is not necessarily a reflection of the number representation. Rather, it can demonstrate the ability of mapping discrete extensive to continuous intensive information. In the absence of an understanding of the continuous intensive properties of numbers (e.g., 3 is one quarter of 12), children resort to a counting-based strategy, in which they use extensive space for the small numbers and then have to “squeeze” the remaining larger numbers on the remaining part of the line. Hence, it would be the adequacy of the proportional reasoning processes that determines the accuracy of the mapping, without assuming anything about the nonlinearity or linearity of the underlying number representations ( Rouder & Geary, 2014 ).
How are numbers and space similar?
Crucially for the link between numbers and space, Newcombe et al. point to structural similarity between number tasks and spatial tasks. Both can be used in an extensive and an intensive way. Developmentally extensive precedes the intensive, so the development from extensive to intensive is necessary in both, and integration of and translation between extensive and intensive is required. Newcombe et al. not only point out that number and space are structurally similar in this respect but also discuss some results that show that spatial skill is predictive of mathematical skill, which suggests a mutually dependent codevelopment.
Why is fraction important?
The case of fractions is no doubt of crucial importance for understanding how a difficulty within the numerical domain can become problematic for everyday performance . Complementing the description by Newcombe et al., we note that the first study performed in adults ( Bonato, Fabbri, Umiltà, & Zorzi, 2007) suggests that university students, when presented with fractions inviting them to focus on the denominator (e.g., 1/3 is larger or smaller than 1/5), reliably present a whole number bias, which is not dissimilar from the one presented by kids. Strikingly, the same pattern of biased processing and difficulty in disengaging from the quantity expressed by the denominator has also been found when testing students of engineering and persists when using more complex ranges of stimuli. This means that, whatever be the reason for the difficulties in fraction processing, it is not abolished, but only circumvented, by formal mathematical training even after several years of formal schooling. In a way, this finding can be interpreted as supporting the idea that formal mathematical education can have “detrimental” effects in processing numbers, which are other than integers.
Why is scientific reasoning important?
The development of scientific reasoning is essential for success in the natural and physical sciences. However, it is also an important capacity for non-STEM students, especially as they engage in problem solving and decision-making across a variety of domains including efforts to evaluate new approaches to teaching and learning, devising alternative modes of mental health services, or evaluating policy information that is relevant to their voting and other forms of civic engagement ( Moore, 2012; Reif & Larkin, 1991 ). Research has shown that university and high school students who are not planning to enter a STEM field show less well-developed scientific reasoning than their STEM oriented peers ( Moore, 2012 ). What is more, estimates suggest that “only about 50 percent of those over 12 years of age who are presented with tests of formal operations perform in what would be considered a formal operational manner. This is true of college-educated adults as well as adolescents. In addition, even people who use formal operational skills on one task may not use them on another.” ( Day, 1981, p. 45; Good, Kronhout, & Mellon, 1979; Huitt & Hummel, 2003 ). Whereas Piaget suggested that the capacity for formal reasoning emerges in adolescence, the research shows that it is neither universally attained nor applied across problem areas. This has led to efforts in secondary and postsecondary education to implement teaching and learning strategies that are intended to enhance scientific reasoning.
How does discrete presentation affect counting?
Although discrete presentation seems to promote a counting strategy, a bias toward thinking extensively has even been observed with completely nonspatial and nonnumerical continuous quantities. In a study on how children combine intensive quantities, Jäger and Wilkening (2001) presented two glasses of colored liquids, one lighter and one darker, to children at the age of 6-, 8-, 10-, and 12 years. Children were asked to imagine the two liquids of equal volume being poured together and to judge the resulting color intensity on a rating scale. An adding rule was predominant in 8- and 10-year-olds, suggesting that children at this age treated color as an extensive quantity and thought that the resulting liquid would be darker than any of its components. Interestingly, 6- and 12-year-olds did not use additive rules nearly as often. This inverse U-shaped developmental trajectory for the adding rule supports the idea that when extensive thinking is emphasized at the beginning of elementary school, access to the continuous intensive system decreases but is slowly regained later, as evidenced by 12-year-olds’ usage of a correct averaging rule. In a second experiment, the authors, additionally, varied the volume of the to-be-combined liquids to investigate children’s and adults’ understanding of how extensive and intensive quantities are interrelated. Children and adults showed interesting misconceptions. For instance, many of them thought the resulting liquid would become darker if more of the same two liquids were mixed together at the same ratio. These findings suggested a persisting confusion when having to simultaneously deal with extensive and intensive quantities, even into adulthood.
Who administered the proportional analogy task to preschoolers?
Building on the idea that children have intuitive understanding of proportionality that is not dependent on formal instruction, Singer-Freeman and Goswami (2001) administered a proportional analogy task to preschool children.
What is proportional reasoning?
Proportional reasoning means that a student is flexible with numbers. When a student can break down numbers easily and see them in different ways, it helps the student solve problems with a variety of strategies and methods. Students need to have a toolkit of strategies to solve problems that they can quickly use.
What does fraction mean in middle school?
As a middle school teacher, another thing that blows students’ minds is the fact that fractions mean division. And teaching how to multiply with fractions, especially a fraction and a whole number is pretty hard, too.
Action Item
Be sure to view the discussion prompt below and engage in a reflection based on the prompts. Sharing your reflection by replying to the discussion prompt is a great way to solidify your new learning and ensure that it sticks instead of washing away like footprints in the sand.
Claim Your Achivement Badge
Once you’ve competed your action item below, be sure to download a copy of your Achievement Badge and be sure to show it off on Twitter, Facebook, Instagram or whatever YOUR favourite social media platform might be!
Are we missing a good definition for proportional reasoning? Don't keep it to yourself..
The ASL fingerspelling provided here is most commonly used for proper names of people and places; it is also used in some languages for concepts for which no sign is available at that moment.
Definitions & Translations
Get instant definitions for any word that hits you anywhere on the web!
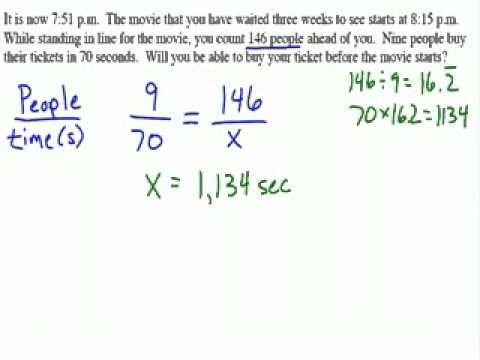
Overview
Reasoning based on relations of proportionality is one form of what in Piaget's theory of cognitive development is called "formal operational reasoning", which is acquired in the later stages of intellectual development. There are methods by which teachers can guide students in the correct application of proportional reasoning.
In mathematics and physics
In mathematics and in physics, proportionality is a mathematical relation between two quantities; it can be expressed as an equality of two ratios:
Functionally, proportionality can be a relationship between variables in a mathematical equation. For example, given the following equation for the force of gravity (according to Newton):
the force of gravity between two masses is directly proportional to the product of the two masse…
Intellectual development
In Piaget's model of intellectual development, the fourth and final stage is the formal operational stage. In the classic book “The Growth of Logical Thinking from Childhood to Adolescence” by Jean Piaget and Barbel Inhelder formal operational reasoning takes many forms, including propositional reasoning, deductive logic, separation and control of variables, combinatorial reasoning, and proportional reasoning. Robert Karplus, a science educator in the 1960s and 197…
Examples
Comparable reasoning patterns exist for inverse proportion.
Typical Solutions
Someone with knowledge about the area of triangles might reason: “Initially the area of the water forming the triangle is 12 since ½ * 4 * 6 = 12. The amount of water doesn’t change so the area won’t change. So the answer is 3 because ½ …
Teaching for Proportional Reasoning
As any experienced teacher will attest , it is not sufficient to simply tell a student his/her answer is incorrect and then instruct the student to use the correct solution. The incorrect strategy has not been “unwired in the brain” and would re-emerge after the current lesson has been completed.
Also the additive strategies noted above cannot simply be labeled as “incorrec…
Expanding Functional Reasoning
The four functional relations noted above, constant sum, constant difference, constant product, and constant ratio, are based on the four arithmetic operations students are most familiar with, namely, addition, subtraction, multiplication and division. Most relations in the real world do not fall into one of these categories. However, if students learn simple techniques such as thought experiments and plotting graphs, they will be able to apply these techniques to more complex sit…