
What does it mean to approach a limit?
To summarize: DEFINITION 2.2. The limit of a function of a variable. We say that a function f(x) approaches a limit L as x approaches c if the sequence of values of x, both from the left and from the right, causes the sequence of values of f(x) to satisfy the definition of "approaches a limit": Definition 2.1.
How do you define the limit of a function?
There are four possible limits to define here. We’ll do one of them and leave the other three to you to write down if you’d like to. Let f (x) f ( x) be a function defined on x > K x > K for some K K. Then we say that, lim x→∞f (x) = ∞ lim x → ∞
What's the difference between at and at in limits?
Just like , the limit of at is . That's because we can still get very very close to and the function's values will get very very close to . So the limit of at is equal to , but the value of at is undefined! They are not the same! That's the beauty of limits: they don't depend on the actual value of the function at the limit.
What is an example of a limit value in math?
Mathematicians have a special notation to indicate they are working with limit values. For example, the answer to Example 1 would be written like this: x x. What is lim x → 0 f ( x) = ? It is tempting to just plug in x = 0 to try to get an answer, but if we try 0 0 is undefined! (Division by zero)
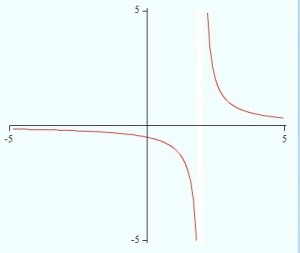
What do the plus and minus mean in limits?
The minus sign indicates "from the left", and the plus sign indicates "from the right". Since the limit of f(x) as x approaches 2 from the right is equal to f(2), f(x) is said to be continuous from the right at 2.
What does 0+ mean in limit?
limt→0+ indicates that the limit is meant to be taken only from the positive direction; it's a one-sided limit. Right hand Limit: limt→0+f(x)=limt→0f(x+|t|). Left Hand Limit: limt→0−f(x)=limt→0f(x−|t|)
What is the symbol for limit?
The symbol lim means we're taking a limit of something.
What does superscript mean in limits?
It means 'implies'. In English it would be: 0
Zero is the integer denoted 0 that, when used as a counting number, means that no objects are present. It is the only integer (and, in fact, the only real number) that is neither negative nor positive. A number which is not zero is said to be nonzero. A root of a function is also sometimes known as "a zero of ."
As a general rule, when you are taking a limit and the denominator equals zero, the limit will go to infinity or negative infinity (depending on the sign of the function).
In calculus and analysis, constants and variables are often reserved for key mathematical numbers and arbitrarily small quantities....Constants and Variables.Symbol NameExplanationExampleeEuler's number ee = 1 0 ! + 1 1 ! + ⋯π (Pi)Archimedes' constantπ 2 6 = 1 1 2 + 1 2 2 + 1 3 2 + 1 4 2 + ⋯9 more rows
Limit of a function means that f(x) can be made to be as close to L as desired, by making x sufficiently close to c. In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L".
partial derivativeThe symbol ∂ indicates a partial derivative, and is used when differentiating a function of two or more variables, u = u(x,t). For example means differentiate u(x,t) with respect to t, treating x as a constant.
A square number is a number multiplied by itself. This can also be called 'a number squared'. The symbol for squared is ².
Positive powersNamePowerNumberone01ten110hundred2100thousand31,00037 more rows
The small "n" is a subscript. When used in the context "Fn," it refers to a function evaluated for the value "n." The text n-1 and n-2 are also subscripts that define previous values of "n" in the sequence. In computer science, subscripts can be used to specify a number system.
The → symbol (right arrow) is used in math to describe a variable approaching another value in the limit operator. The right arrow symbol is typically used in an expression like this. x→nlimf(x) In plain language, this means take the limit of the expression f(x) as the variable x approaches the value n.
∞infinity, the concept of something that is unlimited, endless, without bound. The common symbol for infinity, ∞, was invented by the English mathematician John Wallis in 1655. Three main types of infinity may be distinguished: the mathematical, the physical, and the metaphysical.
The limit of a sum is equal to the sum of the limits. The limit of a difference is equal to the difference of the limits. The limit of a constant times a function is equal to the constant times the limit of the function. The limit of a product is equal to the product of the limits.
The left-hand limit of a function is the value of the function that approaches when the variable approaches its limit from the left. Mathematically it can be written as: lim x → a - f x = m ⇒ lim h → 0 f a - h = m.
For our final limit definition let’s look at limits at infinity that are also infinite in value. There are four possible limits to define here. We’ll do one of them and leave the other three to you to write down if you’d like to.
Note that with both of these definitions there are two ways to deal with the restriction on x x and the one in parenthesis is probably the easier to use, although the main one given more closely matches the definition of the normal limit above.
Definition 6 tells us is that no matter how close to L L we want to get, mathematically this is given by |f (x)−L| <ε | f ( x) − L | < ε for any chosen ε ε , we can find another number M M such that provided we take any x x bigger than M M, then the graph of the function for that x x will be closer to L L than either L−ε L − ε and L +ε L + ε . Or, in other words, the graph will be in the shaded region as shown in the sketch below.
In the previous examples we tried to show that our assumptions satisfied the left inequality by working with it directly. However, in this, the function and our assumption on x x that we’ve got actually will make this easier to start with the assumption on x x and show that we can get the left inequality out of that. Note that this is being done this way mostly because of the function that we’re working with and not because of the type of limit that we’ve got.
So, since continuity, as we previously defined it, is defined in terms of a limit we can also now give a more precise definition of continuity. Here it is,
Also, notice that as the definition points out we only need to make sure that the function is defined in some interval around x = a x = a but we don’t really care if it is defined at x =a x = a. Remember that limits do not care what is happening at the point, they only care what is happening around the point in question.
To consider the limit of a sum of difference, select the limits individually and put them back with the corresponding sign. This fact works regardless of number of functions we seperated by “+” or “-”.
Limits are important in calculus and mathematical analysis and used to define integrals, derivatives, and continuity. It is used in the analysis process, and it always concerns about the behaviour of the function at a particular point. The limit of a sequence is further generalized in the concept of the limit of a topological net and related to ...
If it were zero, it ends up with a division by zero error.
So, what have we learned about limits? Limits are asking what the function is doing around x =a x = a and are not concerned with what the function is actually doing at x = a x = a. This is a good thing as many of the functions that we’ll be looking at won’t even exist at x = a x = a as we saw in our last example.
It is important however, to not get excited about things when the function and the limit do not take the same value at a point.
Likewise, even if a function exists at a point there is no reason (at this point) to think that the limit will have the same value as the function at that point. Sometimes the limit and the function will have the same value at a point and other times they won’t have the same value.
So, while graphs of functions can, on occasion, make your life easier in guessing values of limits they are again probably not the best way to get values of limits. They are only going to be useful if you can get your hands on it and the value of the limit is a “nice” number.
The limit of a function is the value that f ( x) gets closer to as x approaches some number.
Just like the tables, the graph shows that as we get closer to x = 0, the y -value appears to be getting closer to 1 !
There are ways of determining limit values precisely, but those techniques are covered in later lessons. For now, it is important to remember that, when using tables or graphs, the best we can do is estimate.
Thus for the limit of a function to exist as the independent variable approaches c , the left-hand and right-hand limits -- those numbers -- must be equal.
DEFINITION 2.1. The limit of a variable . We say that a sequence of values of a variable v approaches a number l as a limit (a number not a term in the sequence), if, beginning with a certain term vn, and for any subsequent term we might name, the absolute value of vn − l is less than any positive number we name, however small.
The most important limit -- the limit that differential calculus is about -- is called the derivative. All the other limits studied in Calculus I are logical fun and games, never to be heard from again.
DEFINITION 2.2. The limit of a function of a variable.
That sequence also will approach 4. Therefore, the limit of x2 as x approaches 2 both from the right and from the left is the same number. Therefore we can drop the + or − signs and simply write:
We speak of a sequence being infinite, which, in analogy with the sequence of natural numbers, is a brief way of saying that, because of a rule or a pattern or a procedure, there is no limit to the number of terms we coulld name.
We have defined the limit of a variable, but what we often have is a function of a variable -- which is itself a variable. For example,
What does 0+ mean in math?
Can a limit be negative?
What are the symbols in calculus?
How do you read a LIM function?
What does ∂ mean in math?
What is the little 2 above a number called?
What is 1 as a power of 10?
What does a superscript N mean?
What does the arrow in limit mean?
What is the math symbol to represent the infinite?
What are the limit rules?
What is left hand limit?
How many limits are there to infinity?
Which is easier to use: parenthesis or normal limit?
What does definition 6 tell us?
Can assumptions satisfy left inequality?
Is continuity defined in terms of a limit?
Do limits care what is happening at the point?
How to consider the limit of a sum of difference?
Why are limits important in calculus?
What happens if the limit of the denominator is zero?
What have we learned about limits?
Do function and limit take the same value?
Can a function have the same value at a point?
Can graphs of functions be used to get limits?
What is the limit of a function?
What happens when you get closer to x in a graph?
Can you estimate limit values?
Which limits must be equal?
What is the limit of a variable?
What is the most important limit in differential calculus?
What is the definition of 2.2?
Is the limit of x2 as x approaches 2 the same number?
Is a sequence infinite?
Is the limit of a variable a function?

Popular Posts: