Combined variation describes a situation where a variable depends on two (or more) other variables, and varies directly with some of them and varies inversely with others (when the rest of the variables are held constant). For example, if z varies directly as x and inversely as y , we have the following combined variation equation: z = k ( x y)
What is the formula for joint variation?
Solution:
- First set up the equation. a varies jointly with b and c. ...
- Find the value of the constant, k. Given that a = 12 when b = 1 and c = 6
- Rewrite the equation using the value of the constant 'k'
- Using the new equation, find the missing value.
- So, when a varies jointly with b and c and If b = 2 and c = 3, then the value of a is 12.
What is the difference between joint and combined variation?
Joint variation is direct variation to more than one variable (for example, d = (r) (t)). With combined variation, we have both direct variation and indirect variation. joint variation combined variation. Sometimes there are equations or circumstances where you actually have things that vary in more than one element so example of that is in ...
What is joint variation formula?
Joint variation is a more complex relationship between three variables, where one variable varies directly as one variable and inversely as another. The equations expressing combined variation take the form x = ky/z.
How do you calculate the constant of variation?
The direct variation calculator determines:
- Constant of proportionality
- Equation of variation
- Step by step calculations
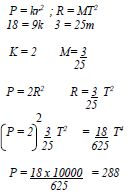
What is combined variation and example?
Example: If x varies directly as y and inversely as z , and x=10 when y=5 and z=3 , for what value of z will x=3 and y=4 ?
What is the variation equation?
A variation is a relation between a set of values of one variable and a set of values of other variables. Direct variation. In the equation y = mx + b, if m is a nonzero constant and b = 0, then you have the function y = mx (often written y = kx), which is called a direct variation.
How do you solve a variation equation?
0:473:54Direct Variation - MathHelp.com - Algebra Help - YouTubeYouTubeStart of suggested clipEnd of suggested clipIf Y varies directly as X and y equals 6 when x equals 4 find K the constant of variation. We knowMoreIf Y varies directly as X and y equals 6 when x equals 4 find K the constant of variation. We know that if Y varies directly as X then we can use the formula y equals KX.
What does K stand for in Y KX?
y=kx is the general form for writing a direct variation. 'y' and 'x' are variables, while 'k' stands for a constant.
What is Joint Variation or Combined Variation?
Joint Variation or Combined Variation is when one quantity varies directly as the product of at least two other quantities.
What is joint variation in algebra?
In Algebra, sometimes we have functions that vary in more than one element. When this happens, we say that the functions have joint variation or combined variation. Joint variation is direct variation to more than one variable (for example, d = (r) (t)). With combined variation, we have both direct variation and indirect variation.
What are some examples of solving variation equations?
Since this is direct variation, the formula is " y = kx2 ".The reason they've given me the data point (x, y) = (2, 8) is that I have to be able to find the value of " k ". So I'll plug in the information they've given me, and solve for k:
What is joint variation?
The other case of variation is "jointly". "Joint variation" means "directly, but with two or more variables". An example would be the formula for the area of a triangle with base " b " and height " h ":
What is inverse variation?
On the other hand, "inverse variation" means that the variable is underneath, in the bottom of a fraction. Suppose, for instance, that you inherit a money market account containing $100,000, and you wonder how much money your rich uncle initially invested eight years ago.
What does "and" mean in math?
Almost always, when you translate word problems from English into math, "and" means "plus" or "added to". But in joint variation, "and" just means "both of these are together on the same side of the fraction" (usually on top), and you multiply.
Is it hard to learn a variation problem?
Variation problems aren't hard once you get the hang of the lingo. The only real difficulty is learning the somewhat specialized vocabulary and the techniques for this classification of problems. Variation problems involve fairly simple relationships or formulas, involving one variable being equal to one term.
Is translating variation problems bad?
Translating variation problems isn't so bad, once you get the hang of it. But then they want you to move on to setting up and solving word problems. These generally fall into two categories: the ones where they want you to find the value of " k ", and the ones where they want you to find some other value, but only after you've found " k " first. Here are some examples:
Can a variation equation have two terms?
So variation equations may have complicated expressions, but they'll only ever have the one term. Their equations will never have two or more terms added together. For instance, y = 3x is a variation equation, but y = 3x + 2 is not. An example of a variation equation would be the formula for the area of the circle: