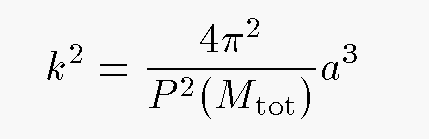
What did Kepler say in his third law?
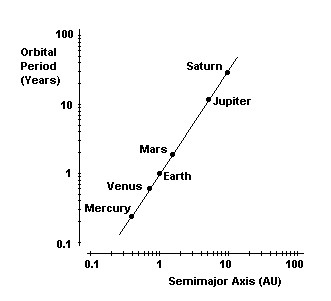
Kepler's third law states that the distance a planet is from the sun, cubed, is directly proportional to the time it takes to complete the orbit, squared. More simply, Kepler found that the distance a planet was located from the sun directly determined the time it took that planet to revolve around the sun.
What are Kepler's 3 laws?
What are Kepler's three laws?
- First law. According to Kepler’s first law, every planet revolves around the sun in an elliptical orbit with the Sun at one focus.
- Second Law. An orbit sweeps an equal area in an equal interval of time.
- Third law. The square of the period of revolution of the planet is proportional to the cube of the semi-major axis of the elliptical orbit.
What are Kepler 3 laws?
Kepler’s Laws of Planetary Motion
- Kepler first law – The law of orbits
- Kepler’s second law – The law of equal areas
- Kepler’s third law – The law of periods
Can someone explain Kepler's third law?
Kepler 's third law - sometimes referred to as the law of harmonies - compares the orbital period and radius of orbit of a planet to those of other planets. Unlike Kepler's first and second laws that describe the motion characteristics of a single planet, the third law makes a comparison between the motion characteristics of different planets.
What is Kepler's law formula?
T = 2 π r 3 G M E . T = 2 π r 3 G M E . For an ellipse, recall that the semi-major axis is one-half the sum of the perihelion and the aphelion. For a circular orbit, the semi-major axis (a) is the same as the radius for the orbit.
What is Kepler's 3rd law in simple terms?
Kepler's Third Law: the squares of the orbital periods of the planets are directly proportional to the cubes of the semi-major axes of their orbits. Kepler's Third Law implies that the period for a planet to orbit the Sun increases rapidly with the radius of its orbit.
Is Kepler's third law correct?
Validity of Kepler's Original Law Kepler's third law in Kepler's original form is approximately valid for the Solar System because the Sun is much more massive than any of the planets and therefore Newton's correction is small.
How do you verify Kepler's third law?
1:064:46Verifying Kepler's Third Law - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo the radius i'll call r from here to here is proportional to t to the power of 2 where it is beingMoreSo the radius i'll call r from here to here is proportional to t to the power of 2 where it is being cubed and the proportional constant between these two variables will be represented as k.
What units is Kepler's third law?
The equation for Kepler's Third Law is P² = a³, so the period of a planet's orbit (P) squared is equal to the size semi-major axis of the orbit (a) cubed when it is expressed in astronomical units.
Why is Kepler's 3rd Law important?
Kepler's third law provides an accurate description of the period and distance for a planet's orbits about the sun.
Johannes Kepler
The first seeds of Kepler’s laws were planted before his 1571 birth in the Free Imperial City of Weil der Stadt, which is now part of the Stuttgart Region in the German state of Baden-Württemberg to father Heinrich Kepler and mother Katharina Guldenmann.
Properties of ellipses laws one and two
One of the keys to understanding Kepler’s laws of planetary motion lies in the properties of ellipses.
What is Kepler's 3rd law?
Kepler's third law provides an accurate description of the period and distance for a planet's orbits about the sun. Additionally, the same law that describes the T 2 /R 3 ratio for the planets' orbits about the sun also accurately describes the T 2 /R 3 ratio for any satellite (whether a moon or a man-made satellite) about any planet. There is something much deeper to be found in this T 2 /R 3 ratio - something that must relate to basic fundamental principles of motion. In the next part of Lesson 4, these principles will be investigated as we draw a connection between the circular motion principles discussed in Lesson 1 and the motion of a satellite.
What were Johannes Kepler's three laws?
Kepler's Three Laws. In the early 1600s, Johannes Kepler proposed three laws of planetary motion. Kepler was able to summarize the carefully collected data of his mentor - Tycho Brahe - with three statements that described the motion of planets in a sun-centered solar system. Kepler's efforts to explain the underlying reasons for such motions are ...
How did Newton Extend His Notion of Gravity to Explain Planetary Motion?
Establishing gravity as the cause of the moon's orbit does not necessarily establish that gravity is the cause of the planet's orbits. How then did Newton provide credible evidence that the force of gravity is meets the centripetal force requirement for the elliptical motion of planets?
How to make an ellipse?
An ellipse can easily be constructed using a pencil, two tacks, a string, a sheet of paper and a piece of cardboard. Tack the sheet of paper to the cardboard using the two tacks. Then tie the string into a loop and wrap the loop around the two tacks. Take your pencil and pull the string until the pencil and two tacks make a triangle (see diagram at the right). Then begin to trace out a path with the pencil, keeping the string wrapped tightly around the tacks. The resulting shape will be an ellipse. An ellipse is a special curve in which the sum of the distances from every point on the curve to two other points is a constant. The two other points (represented here by the tack locations) are known as the foci of the ellipse. The closer together that these points are, the more closely that the ellipse resembles the shape of a circle. In fact, a circle is the special case of an ellipse in which the two foci are at the same location. Kepler's first law is rather simple - all planets orbit the sun in a path that resembles an ellipse, with the sun being located at one of the foci of that ellipse.
What is the special case of an ellipse in which the two foci are at the same location?
In fact, a circle is the special case of an ellipse in which the two foci are at the same location. Kepler's first law is rather simple - all planets orbit the sun in a path that resembles an ellipse, with the sun being located at one of the foci of that ellipse.
What is the third law of harmonies?
Kepler's third law - sometimes referred to as the law of harmonies - compares the orbital period and radius of orbit of a planet to those of other planets. Unlike Kepler's first and second laws that describe the motion characteristics of a single planet, the third law makes a comparison between the motion characteristics of different planets. The comparison being made is that the ratio of the squares of the periods to the cubes of their average distances from the sun is the same for every one of the planets. As an illustration, consider the orbital period and average distance from sun (orbital radius) for Earth and mars as given in the table below.
What are Kepler's laws of motion?
Kepler's three laws of planetary motion can be described as follows: 1 The path of the planets about the sun is elliptical in shape, with the center of the sun being located at one focus. (The Law of Ellipses) 2 An imaginary line drawn from the center of the sun to the center of the planet will sweep out equal areas in equal intervals of time. (The Law of Equal Areas) 3 The ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of their average distances from the sun. (The Law of Harmonies)
What is the equation of Kepler's 3rd law?
The equation of Kepler’s 3rd law is T^2=4pi^2 r^3/GM1. For the full derivatation and more details about Kepler’s 3rd law, watch this:
How did Kepler get his third law?
Kepler, of course, didn’t know any of that. Kepler obtained his third law by carefully doing hand calculations using books of tabulated angular data from Tycho Brahe’s decades of observations of the known planets in the late sixteenth century!
How to find the centripetal force?
Nowadays, you can derive it after the fact for the assumption of CIRCULAR orbits fairly easily. Set the gravitational force from the universal law of gravitation… F = G M m / r 2 … equal to the centripetal force F = m v 2 / r … cancel the “m”… and replace the velocity with distance over the period (2πr/T). Solve for T and you’ll get a relationship between T and r that corresponds to KIII.
Why is the constant of proportionality only approximately the same for each body in the table?
This is because the law itself is a good approximation rather than something absolutely exact.
How many laws of motion are there?
There are three laws of planetary motion given by Johannes Kepler. These laws describe the motion of planets around the Sun.
Which law relates the period of a planetary orbit to the elliptical orbit's semi-?
I’m not sure what the question is actually asking. Kepler’s third law simply relates the period of a planetary orbit to the elliptical orbit’s semi-major axis - that is, that the square of the period is proportional to the cube of the semi-major axis.
Which law states that the orbit of a planet is an ellipse with the Sun at one of the?
First law: The orbit of a planet is an ellipse with the Sun at one of the two foci.
When was Kepler's third law published?
Kepler published his first two laws about planetary motion in 1609, having found them by analyzing the astronomical observations of Tycho Brahe. Kepler's third law was published in 1619. Kepler had believed in the Copernican model of the Solar System, which called for circular orbits, but he could not reconcile Brahe's highly precise observations with a circular fit to Mars' orbit – Mars coincidentally having the highest eccentricity of all planets except Mercury. His first law reflected this discovery.
What is the second law of Kepler?
Kepler had two versions, related in a qualitative sense: the "distance law" and the "area law". The "area law" is what became the Second Law in the set of three; but Kepler did himself not privilege it in that way.
What are the laws of the planets?
The three laws state that: The orbit of a planet is an ellipse with the Sun at one of the two foci. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
What is Kepler's method?
His method involves the solution of a transcendental equation called Kepler's equation .
How many laws did Kepler have?
Figure 1: Illustration of Kepler's three laws with two planetary orbits.
What is the third law?
The third law expresses that the farther a planet is from the Sun, the slower its orbital speed, and vice versa. Isaac Newton showed in 1687 that relationships like Kepler's would apply in the Solar System as a consequence of his own laws of motion and law of universal gravitation .
Which law applies to the brightest moons of Jupiter?
In 1621, Kepler noted that his third law applies to the four brightest moons of Jupiter. Godefroy Wendelin also made this observation in 1643. The second law, in the "area law" form, was contested by Nicolaus Mercator in a book from 1664, but by 1670 his Philosophical Transactions were in its favour. As the century proceeded it became more widely accepted. The reception in Germany changed noticeably between 1688, the year in which Newton's Principia was published and was taken to be basically Copernican, and 1690, by which time work of Gottfried Leibniz on Kepler had been published.
