
How do you simulate from a Markov chain?
One can simulate from a Markov chain by noting that the collection of moves from any given state (the corresponding row in the probability matrix) form a multinomial distribution. One can thus simulate from a Markov Chain by simulating from a multinomial distribution.
What is Markov chain Monte Carlo simulation?
Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability distributions, and have found extensive application in Bayesian statistics.
What is Markov chain in machine learning?
A Markov chain is a discrete-time stochastic process that progresses from one state to another with certain probabilities that can be represented by a graph and state transition matrix P as indicated below:
What is a Markov model?
Markov models are used to model changing systems. There are 4 main types of models, that generalize Markov chains depending on whether every sequential state is observable or not, and whether the system is to be adjusted on the basis of observations made:
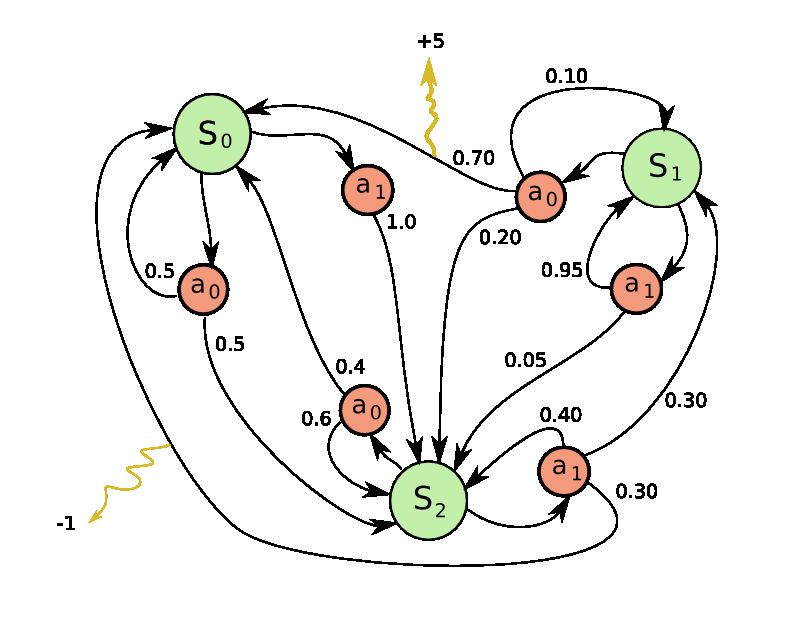
What is Markov chain used for?
Markov Chains are exceptionally useful in order to model a discrete-time, discrete space Stochastic Process of various domains like Finance (stock price movement), NLP Algorithms (Finite State Transducers, Hidden Markov Model for POS Tagging), or even in Engineering Physics (Brownian motion).
What is Markov chain in simple words?
In summation, a Markov chain is a stochastic model which outlines a probability associated with a sequence of events occurring based on the state in the previous event. The two key components to creating a Markov chain are the transition matrix and the initial state vector.
What is Markov chain algorithm?
Markov chain is a systematic method for generating a sequence of random variables where the current value is probabilistically dependent on the value of the prior variable. Specifically, selecting the next variable is only dependent upon the last variable in the chain.
What do you mean by Markov chain analysis?
Markov analysis is a method used to forecast the value of a variable whose predicted value is influenced only by its current state, and not by any prior activity. In essence, it predicts a random variable based solely upon the current circumstances surrounding the variable.
What is Markov chain example?
A game of snakes and ladders or any other game whose moves are determined entirely by dice is a Markov chain, indeed, an absorbing Markov chain. This is in contrast to card games such as blackjack, where the cards represent a 'memory' of the past moves.
What is the importance of Markov chains in data science?
Application of Markov Chains Since Markov chains can be designed to model many real-world processes, they are used in a wide variety of situations. These fields range from the mapping of animal life populations to search engine algorithms, music composition and speech recognition.
Why is it called a Markov chain?
A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov.
What is Markov model in machine learning?
A Hidden Markov Model (HMM) is a statistical model which is also used in machine learning. It can be used to describe the evolution of observable events that depend on internal factors, which are not directly observable.
What is the main application of Markov analysis?
Markov analysis can be used to analyze a number of different decision situations; however, one of its more popular applications has been the analysis of customer brand switching. This is basically a marketing application that focuses on the loyalty of customers to a par- ticular product brand, store, or supplier.
Why is Markov chain used in wind forecasting?
In this case, Markov chain is utilised to predict the probability distribution of wind power or speed in the future based on the current state . It is often reliable for short-term wind forecasting.
When was the network model first used?
Network models as an analog for porous media was first reported 60 years ago ( Fatt, 1956 ), and have gained significant momentum during the last ten years. For the purpose of simulating gas flow in unconventional reservoirs, efforts have been focused on advancing the representativeness and verisimilitude of pore network models to the real pore structures as well as incorporating more flow mechanisms that are beyond viscous flow into the gas flow models.
What are the two classification methods?
Classification methods can be divided into two categories, namely, eager and lazy learners . Given a training set of objects, eager learners establish a general classification model before receiving new objects. If we consider a learning process from the seen to the unseen world, using eager learners trained in the seen world are also ready for recognizing the unseen world and eager to classify new objects (i.e., suppliers). Eager learners include decision tree (DT), Bayesian network (BN), neural networks (NN), AR, and SVM. By contrast, a lazy learner algorithm simply stores the training object or conducts minor processing in the seen world and waits until a new object is given. Lazy learners require an efficient storage technique and can be computationally expensive. CBR classifier is a typical lazy learner. KNN is close to CBR classifier, where the training tuples are stored as points in Euclidean space rather than as cases. On the basis of our review, four classification methods are reported for SS, including DT, BN, NN, and SVM, which are reviewed in Sections 4.3.1.1–4.3.1.4, respectively. In Section 4.3.1.5, we capture three potential classification methods, namely, AR, CBR, and KNN, which have only been reported for SS recently and show potential for future SS applications.
How to simulate a Markov chain?
One can simulate from a Markov chain by noting that the collection of moves from any given state (the corresponding row in the probability matrix) form a multinomial distribution. One can thus simulate from a Markov Chain by simulating from a multinomial distribution.
What is a Markov chain?
A Markov chain is a discrete-time stochastic process that progresses from one state to another with certain probabilities that can be represented by a graph and state transition matrix P as indicated below:
What is a Markov chain?
Markov chains, named after Andrey Markov, are mathematical systems that hop from one "state" (a situation or set of values) to another. For example, if you made a Markov chain model of a baby's behavior, you might include "playing," "eating", "sleeping," and "crying" as states, which together with other behaviors could form a 'state space': ...
How powerful is Markov chain?
In the hands of metereologists, ecologists, computer scientists, financial engineers and other people who need to model big phenomena, Markov chains can get to be quite large and powerful . For example, the algorithm Google uses to determine the order of search results, called PageRank, is a type of Markov chain.
Monte Carlo Markov Chain (MCMC), Explained
MCMC has been one of the most important and popular concepts in Bayesian Statistics, especially while doing inference.
Monte Carlo Sampling
Monte Carlo method derives its name from a Monte Carlo casino in Monaco.
Markov Chains
Before getting into Markov chains, let us have a look over useful property that defines it —
Markov Chains Monte Carlo (MCMC)
MCMC can be used to sample from any probability distribution. Mostly we use it to sample from the intractable posterior distribution for the purpose of Inference.
What is a Markov chain?
A Markov Chain is a mathematical process that undergoes transitions from one state to another. Key properties of a Markov process are that it is random and that each step in the process is “memoryless;” in other words, the future state depends only on the current state of the process and not the past.
Where did the Metropolis algorithm come from?
The name supposedly derives from the musings of mathematician Stan Ulam on the successful outcome of a game of cards he was playing, and from the Monte Carlo Casino in Las Vegas. A Metropolis Algorithm (named after Nicholas Metropolis, a poker buddy of Dr. Ulam) is a commonly used MCMC process.
Why are MCMC methods better than generic Monte Carlo?
While MCMC methods were created to address multi-dimensional problems better than generic Monte Carlo algorithms, when the number of dimensions rises they too tend to suffer the curse of dimensionality: regions of higher probability tend to stretch and get lost in an increasing volume of space that contributes little to the integral. One way to address this problem could be shortening the steps of the walker, so that it doesn't continuously try to exit the highest probability region, though this way the process would be highly autocorrelated and expensive (i.e. many steps would be required for an accurate result). More sophisticated methods such as Hamiltonian Monte Carlo and the Wang and Landau algorithm use various ways of reducing this autocorrelation, while managing to keep the process in the regions that give a higher contribution to the integral. These algorithms usually rely on a more complicated theory and are harder to implement, but they usually converge faster.
What is MCMC in statistics?
In statistics, Markov chain Monte Carlo ( MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by recording states from the chain. The more steps are included, the more closely the distribution of the sample matches the actual desired distribution. Various algorithms exist for constructing chains, including the Metropolis–Hastings algorithm .
Illustrative Example
In this note, we will describe a simple algorithm for simulating Markov chains. We first settle on notation and describe the algorithm in words.
General Algorithm
Here we present a general algorithm for simulating a discrete Markov chain assuming we have S possible states.

Overview
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov.
Introduction
A Markov process is a stochastic process that satisfies the Markov property (sometimes characterized as "memorylessness"). In simpler terms, it is a process for which predictions can be made regarding future outcomes based solely on its present state and—most importantly—such predictions are just as good as the ones that could be made knowing the process's full history. In oth…
History
Markov studied Markov processes in the early 20th century, publishing his first paper on the topic in 1906. Markov processes in continuous time were discovered long before Andrey Markov's work in the early 20th century in the form of the Poisson process. Markov was interested in studying an extension of independent random sequences, motivated by a disagreement with Pavel Nekrasov who claimed independence was necessary for the weak law of large numbers to hold. In his first …
Examples
• Random walks based on integers and the gambler's ruin problem are examples of Markov processes. Some variations of these processes were studied hundreds of years earlier in the context of independent variables. Two important examples of Markov processes are the Wiener process, also known as the Brownian motion process, and the Poisson process, which are considered the most important and central stochastic processes in the theory of stochastic pro…
Formal definition
A discrete-time Markov chain is a sequence of random variables X1, X2, X3, ... with the Markov property, namely that the probability of moving to the next state depends only on the present state and not on the previous states:
if both conditional probabilities are well defined, that is, if
The possible values of Xi form a countable set S called the state space of the c…
Properties
Two states communicate with each other if both are reachable from one another by a sequence of transitions that have positive probability. This is an equivalence relation which yields a set of communicating classes. A class is closed if the probability of leaving the class is zero. A Markov chain is irreducible if there is one communicating class, the state space.
A state i has period if is the greatest common divisor of the number of transitions by which i can b…
Special types of Markov chains
Markov models are used to model changing systems. There are 4 main types of models, that generalize Markov chains depending on whether every sequential state is observable or not, and whether the system is to be adjusted on the basis of observations made:
A Bernoulli scheme is a special case of a Markov chain where the transition probability matrix has identical rows, which means that the next state is independent of even the current state (in addit…
Applications
Research has reported the application and usefulness of Markov chains in a wide range of topics such as physics, chemistry, biology, medicine, music, game theory and sports.
Markovian systems appear extensively in thermodynamics and statistical mechanics, whenever probabilities are used to represent unknown or unmodel…