
Summary.
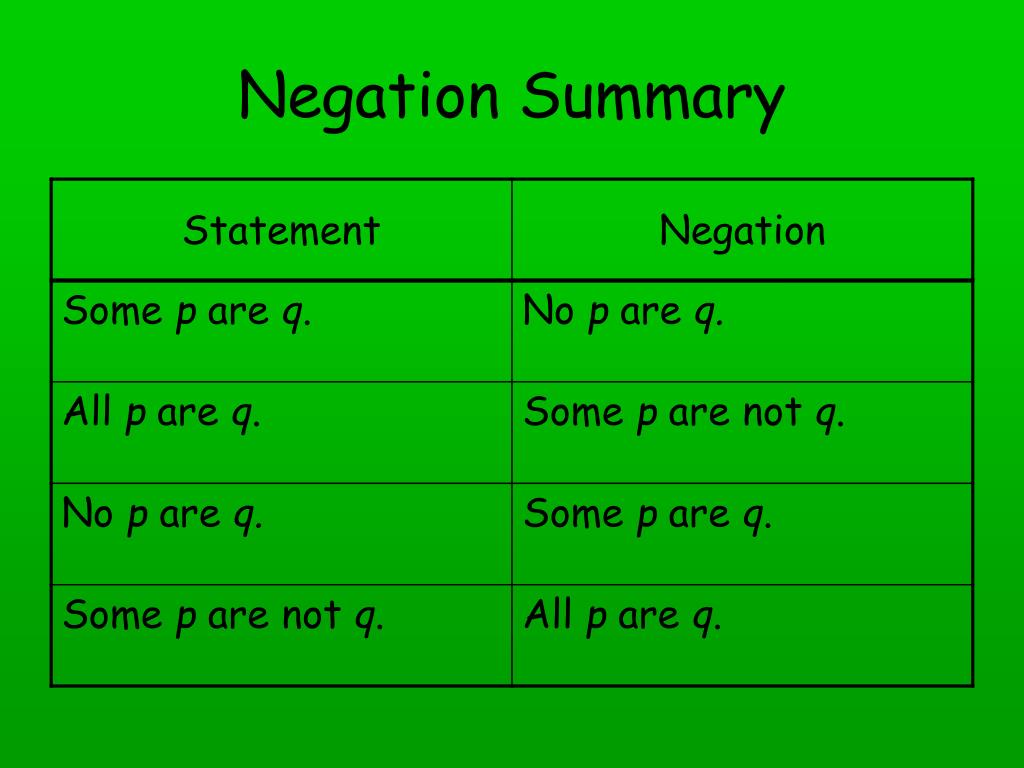
| Statement | Negation |
| "A and B" | "not A or not B" |
| "if A, then B" | "A and not B" |
| "For all x, A (x)" | "There exist x such that not A (x)" |
| "There exists x such that A (x)" | "For every x, not A (x)" |
What is the negation of ∃?
The symbol ∃! means "there exists a unique", and is not really a unit, it carries two conditions: existence and uniqueness. The negation of A and B is not A or not B, in symbols: The negation of "there exists" is "there does not exist". The uniqueness assumes existence, and its negation is plurality.
What is the negation of the square of a number?
The negation of this is that the set of such numbers is empty, i.e. there does not exist a number equal to its square. There exists a number equal to its square (1) and there exists a number not equal to its square (2). Since both these statements are true, they can't be negations of each other.
Is the negation of a statement true?
One thing to keep in mind is that if a statement is true, then its negation is false (and if a statement is false, then its negation is true). Let's take a look at some of the most common negations.
What is the negation of -3 < f(z) ≤ 0?
The negation of a statement is the opposite of the statement. The given statement is "There exists a negative real number z such that − 3 < f ( z) ≤ 0 ." The negation of the quantifier "There exist" is "For every". Also negation of − 3 < f ( z) ≤ 0 is f ( z) ≤ − 3 or f ( z) > 0.
How do you find the negation?
The symbols used to represent the negation of a statement are “~” or “¬”. For example, the given sentence is “Arjun's dog has a black tail”. Then, the negation of the given statement is “Arjun's dog does not have a black tail”. Thus, if the given statement is true, then the negation of the given statement is false.
What is the negation example?
A negation is a statement that cancels out or denies another statement or action. "I didn't kill the butler" could be a negation, along with "I don't know where the treasure is." The act of saying one of these statements is also a negation.
What is the negation of a sentence?
In grammar, negation is when certain words or entire sentences are nullified or shown to be untrue by adding a special type of word called a negative. The most common example is the negative adverb not, used with auxiliary verbs like do or be to negate the original meaning of a sentence.
Is for some the same as there exists?
Yes, they are the same, just as "for all" and "for every" and "for each" mean ∀. They are logically equivalent, but the English language creates a difference, namely that "there exists" is followed by "such that", while "for some" isn't.
What is simple negation give 5 examples?
The most common negative words are no and not. Other negative words include: neither, never, no one, nobody, none, nor, nothing, nowhere: She's never been abroad.
What are 10 examples of negative sentences?
List of Negative SentencesI am not flying to England.That isn't the way to Nashville.They are not from Ecuador.He wasn't eating white rice.We were not sad when he moved away.They don't practice yoga.She did not like Bikhram yoga.He doesn't have to commute to work.More items...
What are the different types of negation?
Types of Sentence Negation "It is usual to distinguish between two types of non-affixal sentence negation in English: firstly, negation with not or -n't; and secondly, negation with the negative words never, neither, nobody, no, none, nor, nothing and nowhere.
What is the negation of at least?
NEGATIONS OF QUANTIFIED STATEMENTS Fact: "None" is the opposite of "at least one." For example: The negation of "Some dogs are poodles" is "No dogs are poodles."
What is the negation of P → Q?
p∨(∼q)
Is there exist correct?
"There exists" works exactly like the more common "there is." Although we use "it" as a subject for verbs describing the weather ("it is raining"; "it is cold"), we usually use "there is" as an introductory statement, and never "it is." There is no reason to doubt this phenomenon.
What is the symbol for there exists?
symbol ∃The symbol ∃ means “there exists”. Finally we abbreviate the phrases “such that” and “so that” by the symbol or simply “s.t.”.
What does there exists mean in math?
The ∃ (there exists) symbol is used in math to express the existence of a variable. For example, the symbol is usually used in an expression like this. ∃x∈N:x is even. In plain language, this expression means there exists a variable x belonging to the set of natural numbers such that x is even.
What is the negation of P → Q?
p∨(∼q)
What do we mean by negation?
Definition of negation 1a : the action or logical operation of negating or making negative. b : a negative statement, judgment, or doctrine especially : a logical proposition formed by asserting the falsity of a given proposition — see Truth Table. 2a : something that is the absence of something actual : nonentity.
What is a negation symbol?
What is the logical negation symbol (¬)? The logical negation symbol is used in Boolean algebra to indicate that the truth value of the statement that follows is reversed. The symbol (¬) resembles a dash with a tail or the upper half of a rectangle.
What is the negation of A and B?
1. The negation of “A or B” is “not(A) and not(B).” 2. The negation of “A and B” is “not(A) or not(B).” 3.
What is negation in math?
Negation. Sometimes in mathematics it's important to determine what the opposite of a given mathematical statement is . This is usually referred to as "negating" a statement. One thing to keep in mind is that if a statement is true, then its negation is false (and if a statement is false, then its negation is true).
What is the negation of the statement "If A, then B"?
The negation of the statement B is "There exists a poor person who is not sad."
How to negate a statement of the form "If A, then B"?
To negate a statement of the form "If A, then B" we should replace it with the statement " A and Not B " . This might seem confusing at first, so let's take a look at a simple example to help understand why this is the right thing to do.
