
What is the formula for the chain rule?
The Chain Rule – At a Glance
- The chain rule allows the users to differentiate two or more composite functions. ...
- The chain rule can be used along with the other rules to derive formulas in certain conditions.
- A new rule can be formed by combining the chain rule with the power rule. ...
What is the function of the chain rule?
Chain rule
- Intuitive explanation. Intuitively, the chain rule states that knowing the instantaneous rate of change of z relative to y and that of y relative to x allows one to calculate ...
- History. ...
- Statement. ...
- Applications. ...
- Higher derivatives. ...
- Proofs. ...
- Multivariable case. ...
- Further generalizations. ...
- See also. ...
- References. ...
How to use the chain rule?
Rule is known as the chain rule because we use it to take derivatives of composites of functions by chaining together their derivatives. The chain rule can be said as taking the derivative of the outer function (which is applied to the inner function) and multiplying it by times the derivative of the inner function. The product rule generally is used if the two ‘parts’ of the function are ...
Do I correctly understand the formula of the chain rule?
Therefore, the chain rule is providing the formula to calculate the derivative of a composition of functions. Let us suppose that f and g are the functions, then the chain rule will express the derivative of their composition. y = f (x) i.e. y is a function of x and y = f (u) i.e. y is a function of u
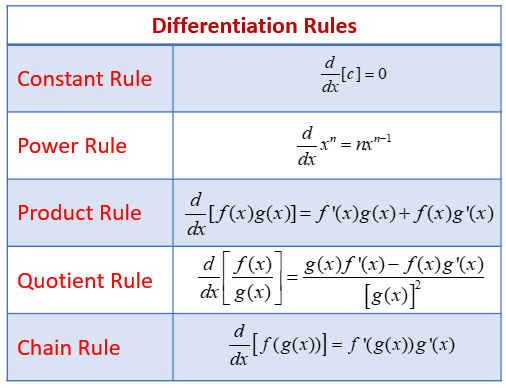
What is the chain rule in simple terms?
The chain rule states that the derivative of f(g(x)) is f'(g(x))⋅g'(x). In other words, it helps us differentiate *composite functions*. For example, sin(x²) is a composite function because it can be constructed as f(g(x)) for f(x)=sin(x) and g(x)=x².
What is the power rule in calculus?
The power rule in calculus is a fairly simple rule that helps you find the derivative of a variable raised to a power, such as: x^5, 2x^8, 3x^(-3) or 5x^(1/2). All you do is take the exponent, multiply it by the coefficient (the number in front of the x), and decrease the exponent by 1. 4:02.
How do you know when to use the power rule or the chain rule?
0:394:17Differences Between the Power Rule & the Chain Rule in CalculusYouTubeStart of suggested clipEnd of suggested clipYes there is that the power rule can only be used with polynomial terms so here is where we'll applyMoreYes there is that the power rule can only be used with polynomial terms so here is where we'll apply the power rule. Okay the original constant in front three. Times the original exponent.
How do you do the chain rule step by step?
Chain RuleStep 1: Identify the inner function and rewrite the outer function replacing the inner function by the variable u. ... Step 2: Take the derivative of both functions. ... Step 3: Substitute the derivatives and the original expression for the variable u into the Chain Rule and simplify. ... Step 1: Simplify.More items...
How do you solve a power rule problem?
0:2512:00The Power Rule For Derivatives - YouTubeYouTubeStart of suggested clipEnd of suggested clipIt's going to equal n times x raised to the n minus one. So let's say for example if f of x is equalMoreIt's going to equal n times x raised to the n minus one. So let's say for example if f of x is equal to x squared. Then the first derivative. We're going to take this constant move it to the front.
Why do we use the chain rule?
The chain rule gives us a way to calculate the derivative of a composition of functions, such as the composition f(g(x)) of the functions f and g.
How do you use the chain rule example?
0:559:24Chain Rule Examples - YouTubeYouTubeStart of suggested clipEnd of suggested clipWe don't write it down so negative 2 times negative 1 is plus 2 x to the and then we decrease theMoreWe don't write it down so negative 2 times negative 1 is plus 2 x to the and then we decrease the exponent by one so it's x to the negative.
How do you do chain rule with exponents?
0:002:22Exponential Functions and the Chain Rule - YouTubeYouTubeStart of suggested clipEnd of suggested clipBut if Y is equal to e to the U where u itself is a function of X then the derivative of Y withMoreBut if Y is equal to e to the U where u itself is a function of X then the derivative of Y with respect to X is e to the U. Times.
How the power rule is formulated?
The power rule for derivatives is that if the original function is xn, then the derivative of that function is nxn−1. To prove this, you use the limit definition of derivatives as h approaches 0 into the function f(x+h)−f(x)h, which is equal to (x+h)n−xnh.
What is the chain rule calculator?
Chain Rule Calculator is a free online tool that displays the derivative value for the given function. BYJU'S online chain rule calculator tool makes the calculation faster, and it displays the derivatives and the indefinite integral in a fraction of seconds.
Is the chain rule difficult?
The difficulty in using the chain rule: Implementing the chain rule is usually not difficult. The problem that many students have trouble with is trying to figure out which parts of the function are within other functions (i.e., in the above example, which part if g(x) and which part is h(x).
What is the power rule?
The general power rule is a special case of the chain rule. It is useful when finding the derivative of a function that is raised to the nth power. The general power rule states that this derivative is n times the function raised to the (n-1)th power times the derivative of the function. chain rule composite functions power functions power rule ...
What is the chain rule in calculus?
The chain rule is one of the toughest topics in Calculus and so don't feel bad if you're having trouble with it. Because it's so tough I've divided up the chain rule to a bunch of sort of sub-topics and I want to deal with a bunch of special cases of the chain rule, and this one is going to be called the general power rule.
What is the chain rule?
Chain rule lets us calculate derivatives of equations made up of nested functions, where one function is the “outside” function and one function is the “inside function.
What is the chain rule in calculus?
Chain rule lets us calculate derivatives of equations made up of nested functions, where one function is ...
How many steps are required to apply the chain rule?
So applying the chain rule requires just two simple steps.
What is the chain rule?
Chain rule. The chain rule tells us how to find the derivative of a composite function. Brush up on your knowledge of composite functions, and learn how to apply the chain rule correctly. It tells us how to differentiate composite functions.
What is the chain rule for composite function?
Notice that is a composite function: Because is composite, we can differentiate it using the chain rule: Described verbally, the rule says that the derivative of the composite function is the inner function within the derivative of the outer function , multiplied by the derivative of the inner function . Before applying the rule, let's find the ...
Does Khan Academy keep 100% of donations?
Yes, I'll generously add $0.25 each month to cover the transaction fees so Khan Academy can keep 100% of my donation. To defend against fraud, we use Google reCAPTCHA, which could not be loaded. To donate, you may need to temporarily disable your adblocker and restart your browser.
What is the chain rule?
As the name suggests, chain rule means differentiating the terms one by one in a chain form, starting from the outermost function to the innermost function. Let us illustrate this rule with the help of an example:
What is chain rule in differential calculus?
Similarly, in differential calculus, chain rule is a formula used to find the derivative of a composite function. So before starting the formula of chain rule, let us understand the meaning of composite function and how it can be differentiated.
What is the chain rule for total derivatives?
The chain rule for total derivatives implies a chain rule for partial derivatives. We know that the partial derivative in the ith coordinate direction can be evaluated by multiplying the ith basis vector’s Jacobian matrix when the total derivative exists. Hence, the chain rule for the function y = f (u) = (f1(u), …, fk(u)) and u = g (x) = (g1(x), …, gm(x)) can be written for partial derivatives as:
What is the rule for finding the derivative of composition of function?
The rule applied for finding the derivative of composition of function is basically known as the chain rule. Let f represent a real valued function which is a composition of two functions u and v such that:
What is the Chain Rule?
The chain rule is used to calculate the derivative of a composite function. The chain rule formula states that dy/dx = dy/du × du/dx. In words, differentiate the outer function while keeping the inner function the same then multiply this by the derivative of the inner function.
How to Do the Chain Rule
Differentiate the outer function, keeping the inner function the same.
The Chain Rule with Trigonometry
The chain rule is used to differentiate trigonometric functions containing another function. Differentiate the trigonometric function, keeping the inner function the same and then multiply this by the derivative of the inner function.
The Chain Rule with Exponential Functions
The derivative of y = e𝑥 is dy/d𝑥 = e𝑥 and so using the chain rule, the derivative of y = ef(𝑥) is dy/d𝑥 = f' (𝑥 ). ef(𝑥). Simply differentiate the power of e and multiply this by the original function.
Applying the Chain Rule with Three Functions
The chain rule can be applied to the composition of three functions. If y (𝑥) = h (g (f (x))), then y' (𝑥) = f' (𝑥) . g' (f (𝑥)) . h' (g (f (𝑥))). However, it is easier to apply the chain rule twice to differentiate three functions.
Chain Rule Examples with Solutions
Here are some examples of using the chain rule to differentiate a variety of functions:
When to Use the Chain Rule
The chain rule is used to differentiate any composite function of the form y = f (g (𝑥)). That is a function that has an inner function with an outer function applied to it. For example y = (3𝑥 + 2)5 is made of the functions g (𝑥) = 3𝑥 + 2 and f (𝑥) = 𝑥5.
