What is De Morgan’s law?
De Morgan’s Law states that the complement of the union of two sets is the intersection of their complements, and also, the complement of intersection of two sets is the union of their complements. These laws are named after the Greek Mathematician “De Morgan”. What is De Morgan’s Law?
What are De Morgan’s laws of set theory?
In set theory, these laws relate the intersection and union of sets by complements. De Morgan’s Laws Statement and Proof A well-defined collection of objects or elements is known as a set. Various operations like complement of a set, union and intersection can be performed on two sets.
What is De Morgan’s first law of complement?
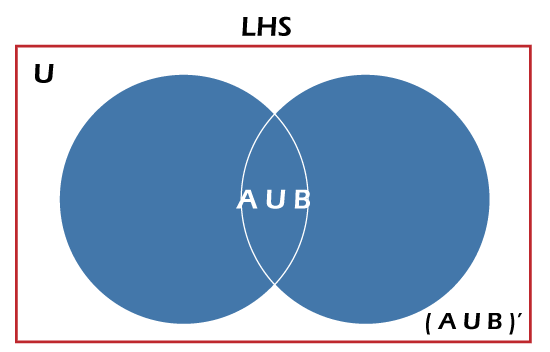
According to De Morgan’s first law, the complement of the union of two sets A and B is equal to the intersection of the complement of the sets A and B. Where A’ denotes the complement.
Why is John De Morgan so important?
Still, De Morgan is given credit for stating the laws in the terms of modern formal logic, and incorporating them into the language of logic. De Morgan's laws can be proved easily, and may even seem trivial.

What is the purpose of De Morgan Theorem?
De Morgan's Theorem, T12, is a particularly powerful tool in digital design. The theorem explains that the complement of the product of all the terms is equal to the sum of the complement of each term. Likewise, the complement of the sum of all the terms is equal to the product of the complement of each term.
What is the statement of De Morgan law?
According to De Morgan's first law, the complement of the union of two sets A and B is equal to the intersection of the complement of the sets A and B. Where A' denotes the complement. This law can be easily visualized using Venn Diagrams.
What is De Morgan's theorem explain with an example?
Explain De Morgan's theorem It is used to solve Boolean Algebra expressions. It perfomes gate operation like NAND gate and NOR gate. Example: If A and B are the inputs then, A.B = Aˉ + Bˉ Here the result of OR'ing variables A and B together is equivalent to AND'ing the complements of the individual variables A and B.
What is De Morgan first law?
In algebra, De Morgan's First Law or First Condition states that the complement of the product of two variables is corresponding to the sum of the complement of each variable. In other words, according to De-Morgan's first Laws or first theorem if 'A' and 'B' are the two variables or Boolean numbers.
What is De Morgan's first law?
It states that the complement of the union of any two sets is equal to the intersection of the complement of that sets.
What is De Morgan's Second law?
It states that the complement of the intersection of any two sets is equal to the union of the complement of that sets.
Why De Morgan's law is used?
De Morgan's law is used for a better understanding of the multiple set operations and their inter-relationship in set theory.
What are the fundamental operations of the set used for De Morgan's law?
The fundamental operations like the union of sets, the intersection of sets and the complement of sets are used in De Morgan's law.
What are De Morgan's laws?
The De Morgans' Laws are: 1. ({(AUB)^prime } = {A^prime } cap {B^prime }) 2. ({(AUB)^prime } = {A^prime } cap {B^prime }.)
What does De Morgan’s first law state?
De Morgan’s first law states that the complement of the union of two sets A and B is equal to the intersection of the complement of the sets A and B.
How to express De Morgan’s first law?
If A and B are the two sets, then De Morgan’s first law is expressed as (AUB)’= A’∩B’.
What is De Morgan’s first law in boolean algebra?
In boolean algebra, De Morgan’s first law states that “if two (or more) input variables are AND’ed and negated, it should be equivalent to the OR o...
What is De Morgan's law?
Still, De Morgan is given credit for stating the laws in the terms of modern formal logic, and incorporating them into the language of logic. De Morgan's laws can be proved easily, and may even seem trivial. Nonetheless, these laws are helpful in making valid inferences in proofs and deductive arguments.
What is the resultant set of De Morgan's laws?
De Morgan's laws represented with Venn diagrams. In each case, the resultant set is the set of all points in any shade of blue.
Which theorem is applied to the negation of a disjunction or the negation of a?
De Morgan's theorem may be applied to the negation of a disjunction or the negation of a conjunction in all or part of a formula.
What is the mnemonic for De Morgan's laws?
In set notation, De Morgan's laws can be remembered using the mnemonic "break the line, change the sign".
What does the symbol "de Morgan" mean?
is a metalogical symbol meaning "can be replaced in a logical proof with". Applications of the rules include simplification of logical expressions in computer programs and digital circuit designs. De Morgan's laws are an example of a more general concept of mathematical duality .
Who invented the laws of logic?
The laws are named after Augustus De Morgan (1806–1871), who introduced a formal version of the laws to classical propositional logic. De Morgan's formulation was influenced by algebraization of logic undertaken by George Boole, which later cemented De Morgan's claim to the find.
Is De Morgan's theorem a disjunction?
The application of De Morgan's theorem to a conjunction is very similar to its application to a disjunction both in form and rationale. Consider the following claim: "it is false that A and B are both true", which is written as:
Set Theory Operations
To understand what De Morgan’s Laws say, we must recall some definitions of set theory operations. Specifically, we must know about the union and intersection of two sets and the complement of a set.
Example of De Morgan's Laws
For example, consider the set of real numbers from 0 to 5. We write this in interval notation [0, 5]. Within this set we have A = [1, 3] and B = [2, 4]. Furthermore, after applying our elementary operations we have:
Naming of De Morgan's Laws
Throughout the history of logic, people such as Aristotle and William of Ockham have made statements equivalent to De Morgan's Laws.
How are De Morgan's laws related?
De Morgan's Laws describe how mathematical statements and concepts are related through their opposites. In set theory, De Morgan's Laws relate the intersection and union of sets through complements. In propositional logic, De Morgan's Laws relate conjunctions and disjunctions of propositions through negation. De Morgan's Laws are also applicable in computer engineering for developing logic gates.
Can De Morgan's laws be generalized?
De Morgan's Laws can be generalized to any number of sets.
What is the De Morgan theorem?
We may apply De Morgan’s theorem t o negating a dis-junction or the negation of conjunction in all or part of a formula. This theorem explains that the complement of all the terms’ product is equal to the sum of each term’s complement. Similarly, the complement of the sum of all the terms is equal to the product of the complement of each term. Also, this theorem is used to solve different problems in boolean algebra.
Can equation 1 be represented by Venn diagram?
Similarly, R.H.S of equation 1 can be represented using Venn Diagrams as well, the first part i.e., A’ can be depicted as follows:
What are De Morgan's rules?
In propositional logic and Boolean algebra, De Morgan's are a pair of transformation rules that are both valid rules of inference. The rules allow the expression of conjunctions and disjunctions purely in terms of each other via negation.
What are the consequences of DeMorgan's laws?
One important consequence of DeMorgan's laws is that, since all logical operations can be expressed in terms of AND, OR, and NOT, all logical operations can also be expressed in terms of just AND and NOT, or just OR and NOT.
Is Morgan's theorem easy to realize?
I want to share an experience where I realized that De Morgan's theorem is not easy to realize but is really very critical in solving problems.
What are De Morgan's laws?
De Morgan’s Laws are the most important rules of Set Theory and Boolean Algebra. This post will discuss in detail about what are De Morgan’s Laws, details about first law and second Law, verification of these laws and their applications.
What were the major mathematical works of De Morgan?
De Morgan’s texts were outstanding which included Algebra, Trigonometry, Differential and Integral Calculus, Probability and Symbolic Logic. De Morgan pioneered Propositional Calculus. He devised Algorithm for approximating factorials in the 19th Century.
What is the first law of union?
The first law or the Law of Union states that: If A and B are two finite sets or subsets of a Universal Subset U then, the element not in A ∪ B is not in A’ and not in B’. Conversely, it also states that an element not in A’ and not in B’ is not in A ∪ B. i.e.
Who is Augustus De Morgan?
Augustus De Morgan was a British Mathematician who formulated laws or rules of Set Theory and Boolean Algebra that relates three basic ‘Set’ operations; Union, Intersection and Complement. De Morgan laws are a couple of theorems that are related to each other. In Propositional Logic and Boolean Algebra, these laws are seen as rules ...
How do the laws relate to conjunction and inclusive disjunction?
The laws relate conjunction and inclusive dis-junction through Negation.

Overview
In propositional logic and Boolean algebra, De Morgan's laws are a pair of transformation rules that are both valid rules of inference. They are named after Augustus De Morgan, a 19th-century British mathematician. The rules allow the expression of conjunctions and disjunctions purely in terms of each other via negation.
Formal notation
The negation of conjunction rule may be written in sequent notation:
,
and
.
The negation of disjunction rule may be written as:
History
The laws are named after Augustus De Morgan (1806–1871), who introduced a formal version of the laws to classical propositional logic. De Morgan's formulation was influenced by algebraization of logic undertaken by George Boole, which later cemented De Morgan's claim to the find. Nevertheless, a similar observation was made by Aristotle, and was known to Greek and Medieval logicians. For example, in the 14th century, William of Ockham wrote down the words th…
Informal proof
De Morgan's theorem may be applied to the negation of a disjunction or the negation of a conjunction in all or part of a formula.
In the case of its application to a disjunction, consider the following claim: "it is false that either of A or B is true", which is written as:
In that it has been established that neither A nor B is true, then it must follow that both A is not tr…
Formal proof
Here we use to denote the complement of A. The proof that is completed in 2 steps by proving both and .
Let . Then, .
Because , it must be the case that or .
If , then , so .
Generalising De Morgan duality
In extensions of classical propositional logic, the duality still holds (that is, to any logical operator one can always find its dual), since in the presence of the identities governing negation, one may always introduce an operator that is the De Morgan dual of another. This leads to an important property of logics based on classical logic, namely the existence of negation normal forms: any formula …
In intuitionistic logic
Three out of the four implications of de Morgan's laws hold in intuitionistic logic. Specifically, we have
and
while the converse of the last implication does not hold in pure intuitionistic logic and would be equivalent to the law of the weak excluded middle
See also
• Isomorphism – NOT operator as isomorphism between positive logic and negative logic
• List of Boolean algebra topics
• List of set identities and relations
• Positive logic