What does the side splitter theorem state?
The side splitter theorem states that if a line is parallel to a side of a triangle and the line intersects the other two sides, then this line divides those two sides proportionally. The side splitter theorem is a natural extension of similarity ratio, and it happens any time that a pair of parallel lines intersect a triangle.
How to solve 45-45-90 triangles?
When given the length of the hypotenuse of a 45°-45°-90° triangle, you can calculate the side lengths by simply dividing the hypotenuse by √2. Note: Only the 45°-45°-90° triangles can be solved using the 1:1: √2 ratio method .
Is there converse for side splitter theorem?
Triangle Proportionality Theorem Converse: If a line divides two sides of a triangle proportionally, then it is parallel to the third side. What is a side splitter? Answer: The side splitter theorem states that if a line is parallel to a side of a triangle and the line intersects the other two sides , then this line divides those two sides proportionally.
What is the converse of side splitter theorem?
The converse of side splitter theorem states that if a line divides two sides proportionally, then that line is parallel to the third side. The ratio in which TU divides the two sides is It means the line TU divides two sides proportionally. Using converse of side splitter theorem, Line segment TU is parallel to line segment RS because

What does side splitter theorem say?
(Side Splitter Theorem): If a line is parallel to a side of a triangle and intersects the other two sides, then this line divides those two sides proportionally.
How do you prove the side splitter theorem?
2:569:27Side Splitter Theorem Proof - YouTubeYouTubeStart of suggested clipEnd of suggested clipThe longer side to the shorter side of the smaller triangle CB. Will be proportional to the length CMoreThe longer side to the shorter side of the smaller triangle CB. Will be proportional to the length C e2 the shorter side CD. And this would be the proportion.
When can you use the side splitter theorem?
The side splitter theorem states that if a line is parallel to a side of a triangle and the line intersects the other two sides, then this line divides those two sides proportionally.
How do you find a side splitter?
3:1923:53Triangle Proportionality Theorem, Side Splitter Theorem & Angle ...YouTubeStart of suggested clipEnd of suggested clipSo ac is one side of the triangle. And intersects the other two sides. So this line d e intersectsMoreSo ac is one side of the triangle. And intersects the other two sides. So this line d e intersects sides a b and b c those are the other two sides.
What is the formula for 30 60 90 triangle?
The sides of a 30-60-90 triangle are always in the ratio of 1:√3: 2. This is also known as the 30-60-90 triangle formula for sides y: y√3: 2y. Let us learn the derivation of this ratio in the 30-60-90 triangle proof section. This formula can be verified using the Pythagoras theorem.
What is the meaning of midline theorem?
The midline theorem claims that cutting along the midline of a triangle creates a segment that is parallel to the base and half as long.
Which theorem can prove the similarity between two triangles?
In total, there are 3 theorems for proving triangle similarity: AA Theorem. SAS Theorem. SSS Theorem.
How do you find the missing side of a triangle?
Given two sidesif leg a is the missing side, then transform the equation to the form when a is on one side, and take a square root: a = √(c² - b²)if leg b is unknown, then. b = √(c² - a²)for hypotenuse c missing, the formula is. c = √(a² + b²)
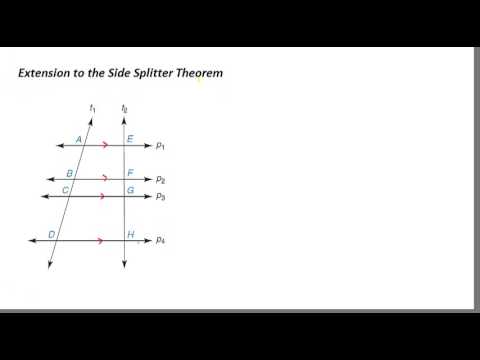
What is the three parallel lines theorem?
Three Parallel Lines Theorem If three parallel lines intersect two transversals, then they divide the transversals proportionally.
How do you find the missing length of a side splitter theorem?
12:4720:10Day 8 HW #1 to #6 Side Splitter Theorem of Similar TrianglesYouTubeStart of suggested clipEnd of suggested clipSo the 6 over 2 should equal 9 over X so then we'll just call it cross multiply. So that'll be 6x isMoreSo the 6 over 2 should equal 9 over X so then we'll just call it cross multiply. So that'll be 6x is equal to 18. And then just divide both sides by 6. So X is equal to 3.Day 8 HW #1 to #6 Side Splitter Theorem of Similar Triangleshttps://www.youtube.com › watchhttps://www.youtube.com › watch
What is the SAS similarity theorem?
SAS or Side-Angle-Side Similarity If the two sides of a triangle are in the same proportion of the two sides of another triangle, and the angle inscribed by the two sides in both the triangle are equal, then two triangles are said to be similar.Similar Triangles- Formula, Theorem & Proof of SSS, SAS AAA Similarityhttps://byjus.com › maths › similar-triangleshttps://byjus.com › maths › similar-triangles
What is hinge Theorem?
The Hinge Theorem states that if two sides of two triangles are congruent and the included angle is different, then the angle that is larger is opposite the longer side.Hinge theorem - Yup Mathhttps://yup.com › math-resources › hinge-theoremhttps://yup.com › math-resources › hinge-theorem
How do you prove that a line parallel to one side of a triangle divides the other two sides proportionally and converse?
If a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides these two sides proportionally. If ¯DE∥¯BC , then ADDB=AEEC .
How do you prove the angle bisector theorem?
0:365:22Proof: The Angle Bisector Theorem - YouTubeYouTubeStart of suggested clipEnd of suggested clipLet's go ahead and write this out in a two column proof. So here we're given that ray a d bisectsMoreLet's go ahead and write this out in a two column proof. So here we're given that ray a d bisects angle bac. And that ray a b is perpendicular to segment ed. And ray ac is perpendicular to segment fd.
How does the triangle angle bisector theorem work?
The angle bisector of a triangle divides the opposite side into two parts proportional to the other two sides of the triangle. In a triangle, if the interior point is equidistant from the two sides of a triangle, then that point lies on the angle bisector of the angle formed by the two line segments.
What is the SAS Similarity theorem?
SAS or Side-Angle-Side Similarity If the two sides of a triangle are in the same proportion of the two sides of another triangle, and the angle inscribed by the two sides in both the triangle are equal, then two triangles are said to be similar.
How to calculate side splitter theorem?from calculator.academy
The following example shows the steps and information needed to calculate the missing length of a triangle that has been split.
When three parallel lines intersect two transversals, what is the corollary of the theorem?from mathwarehouse.com
Answer: A corollary of the this theorem is that when three parallel lines intersect two transversals, then the segments intercepted on the transversal are proportional.
What happens when red segments are parallel?from mathwarehouse.com
If the red segments are parallel, then they 'split' or divide triangle's sides proportionally. However, when you try to set up the proportion, you will se that it is not true:
When 2 lines are cut by a transversal and the corresponding angles are congruent, the lines are?from mathbitsnotebook.com
12. If 2 lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel.
Does the segment in the midpoint theorem connect the midpoints of the sides?from mathbitsnotebook.com
While this theorem may look somewhat like the "mid-segment" theorem, the segment in this theorem does not necessarily connect the "midpoints" of the sides.
What is the side splitter theorem?
It tells us that: If a line is parallel to one side of a triangle and intersects the other two sides, it divides those two sides into proportional segments.
Can we use the side splitter theorem to find the length of BD?
4.) We can now apply the side splitter theorem to find the length of BD.
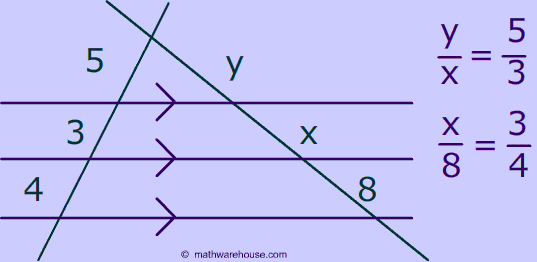
What is the side splitter theorem?from mathwarehouse.com
The "Side Splitter" Theorem says that if a line intersects two sides of a triangle and is parallel to the third side of the triangle, it divides those two sides proportionally. Find x.
When three parallel lines intersect two transversals, what is the corollary of the theorem?from mathwarehouse.com
Answer: A corollary of the this theorem is that when three parallel lines intersect two transversals, then the segments intercepted on the transversal are proportional.
What happens when red segments are parallel?from mathwarehouse.com
If the red segments are parallel, then they 'split' or divide triangle's sides proportionally. However, when you try to set up the proportion, you will se that it is not true:
When 2 lines are cut by a transversal and the corresponding angles are congruent, the lines are?from mathbitsnotebook.com
12. If 2 lines are cut by a transversal and the corresponding angles are congruent, the lines are parallel.
Does the segment in the midpoint theorem connect the midpoints of the sides?from mathbitsnotebook.com
While this theorem may look somewhat like the "mid-segment" theorem, the segment in this theorem does not necessarily connect the "midpoints" of the sides.
Does a side splitter apply to the bottoms?from mathwarehouse.com
NOTE: The side splitter only applies to the intercepted sides. It does not apply to the "bottoms" .