is ridge regression biased

Ridge regression is a term used to refer to a linear regression model whose coefficients are not estimated by ordinary least squares (OLS

), but by an estimator, called ridge estimator, that is biased but has lower variance than the OLS estimator.

Full Answer

What is ridge regression?

Which model is Ridge Estimation?

What is the mean squared error of a ridge estimator?

Which estimator has the lowest variance?

What is ridge estimator?

Is the mean squared error of the ridge estimator smaller than the OLS?

Is the ridge estimator unbiased?

See 2 more

Why is ridge regression preferred?

Ridge regression is a better predictor than least squares regression when the predictor variables are more than the observations. The least squares method cannot tell the difference between more useful and less useful predictor variables and includes all the predictors while developing a model.

Is Ridge better than OLS?

the researchers recommended the ridge regression method rather than OLS because it provides a better estimate than OLS when independent variables are related without omitting any of the independent variables.

Why ridge regression is better than linear regression?

First is due to the biased and second is due to the variance. Prediction error can occur due to any one of these two or both components. Here, we'll discuss about the error caused due to variance. Ridge regression solves the multicollinearity problem through shrinkage parameter λ (lambda).

Does lasso regression reduce bias?

Lasso regression is another extension of the linear regression which performs both variable selection and regularization. Just like Ridge Regression Lasso regression also trades off an increase in bias with a decrease in variance.

What are the limitations of ridge regression?

Limitation of Ridge Regression: Ridge regression decreases the complexity of a model but does not reduce the number of variables since it never leads to a coefficient been zero rather only minimizes it. Hence, this model is not good for feature reduction.

Does Ridge prevent overfitting?

L2 Ridge Regression It is a Regularization Method to reduce Overfitting. We try to use a trend line that overfit the training data, and so, it has much higher variance then the OLS. The main idea of Ridge Regression is to fit a new line that doesn't fit the training data.

Is ridge regression sensitive to outliers?

The ridge estimator is very susceptible to outliers, much like the OLS estimator. The reason for that is that we still depend on the least squares minimization technique and this does not allow large residuals. Hence the regression line, plane or hyperplane will be drawn towards the outliers.

Does ridge regression fix multicollinearity?

Specifically, highly correlated variables can be used together, with ridge regression used to reduce the multicollinearity.

Should I use ridge or lasso regression?

Lasso tends to do well if there are a small number of significant parameters and the others are close to zero (ergo: when only a few predictors actually influence the response). Ridge works well if there are many large parameters of about the same value (ergo: when most predictors impact the response).

Why is lasso regression biased?

LASSO regression implementation We observe that, as the regularization parameter alpha increases, the norm of the regression coefficients become smaller and smaller. This means more regression coefficients are forced to zero, which tends to increases bias error (over simplification).

How do you reduce bias in regression?

Reducing BiasChange the model: One of the first stages to reducing Bias is to simply change the model. ... Ensure the Data is truly Representative: Ensure that the training data is diverse and represents all possible groups or outcomes. ... Parameter tuning: This requires an understanding of the model and model parameters.

Is lasso unbiased?

Lasso is biased because it penalizes all model coefficients with the same intensity. A large coefficient and a small coefficient are shrunk at the same rate. This biases estimates of large coefficients which should remain in the model. Under specific conditions, the bias of large coefficients is λ (slide 2).

Is OLS the best estimator?

An estimator that is unbiased and has the minimum variance is the best (efficient). The OLS estimator is the best (efficient) estimator because OLS estimators have the least variance among all linear and unbiased estimators.

What is the difference between OLS and ridge regression?

Ridge regression is a term used to refer to a linear regression model whose coefficients are estimated not by ordinary least squares (OLS), but by an estimator, called ridge estimator, that, albeit biased, has lower variance than the OLS estimator.

When would you use Ridge and lasso regression instead of OLS?

Lasso tends to do well if there are a small number of significant parameters and the others are close to zero (ergo: when only a few predictors actually influence the response). Ridge works well if there are many large parameters of about the same value (ergo: when most predictors impact the response).

Why is OLS the best?

According to Hansen, OLS has the lowest sampling variance among all unbiased estimators, both linear and non-linear. In other words, OLS is BUE—the best unbiased estimator.

Ridge Regression Explained, Step by Step - Machine Learning Compass

Ridge Regression is an adaptation of the popular and widely used linear regression algorithm. It enhances regular linear regression by slightly changing its cost function, which results in less overfit models. In this article, you will learn everything you need to know about Ridge Regression, and how you can start using it in your own machine learning projects.

What is ridge regression?

Ridge Regression is an adaptation of the popular and widely used linear regression algorithm. It enhances regular linear regression by slightly changing its cost function, which results in less overfit models. In this article, you will learn everything you need to know about Ridge Regression, and how you can start using it in your own machine learning projects.

What is the goal of linear regression?

The goal of linear regression is to fit a line to a dataset in such a way that it minimizes the mean squared error of our line and our data. With regular linear regression, we don’t tell our model anything about how it should achieve this goal. We just want to minimize the MSE and that’s it. We don’t really care whether the model parameters in our model are very large or very small, we don’t care about overfitting, and so on.

What is the purpose of lasso and ridge?

The purpose of lasso and ridge is to stabilize the vanilla linear regression and make it more robust against outliers, overfitting, and more. Lasso and ridge are very similar, but there are also some key differences between the two that you really have to understand if you want to use them confidently in practice.

Is idealized model better than OLS model?

Alright, that looks better! Our idealized model does seem to have a slightly higher bias than our OLS model, but it also has a lot lower variance. We can confirm this by looking at the MSE of both models on the training and testing data and then compare the relative difference of the errors for training and testing, which, as we know from the article about bias and variance , is a good measure to intuitively get a feel for the variance of a model. If we do this, we get the following results:

Can gradient descent be reused?

We can reuse the gradient descent function that we’ve implemented in the article about Gradient Descent for Linear Regression . Here’s how the code looked like:

Is there a normal equation for ridge regression?

The good news here is that there is a normal equation for ridge regression. Let’s recall how the normal equation looked like for regular OLS regression:

Is a ridge model more sensitive to changes in input data than an OLS model?

We can see how ridge is less sensitive to changes in the input data than OLS regression. Therefor we can conclude that ridge models have a lower variance than OLS models. However, because of the penalty term, they usually have a slightly higher bias than OLS models.

Why is ridge regression hard to interpret?

Since some predictors will get shrunken very close to zero, this can make it hard to interpret the results of the model. In practice, ridge regression has the potential to produce a model that can make better predictions compared to a least squares model but it is often harder to interpret the results of the model.

What is the benefit of ridge regression?

The biggest benefit of ridge regression is its ability to produce a lower test mean squared error (MSE) compared to least squares regression when multicollinearity is present .

What variables are used in a linear regression model?

In ordinary multiple linear regression, we use a set of p predictor variables and a response variable to fit a model of the form:

What should be the standard deviation of a ridge regression?

Before performing ridge regression, we should scale the data such that each predictor variable has a mean of 0 and a standard deviation of 1. This ensures that no single predictor variable is overly influential when performing ridge regression.

What language is used to perform ridge regression?

The following tutorials explain how to perform ridge regression in R and Python, the two most common languages used for fitting ridge regression models:

When does shrinkage penalty become more influential?

When λ = 0, this penalty term has no effect and ridge regression produces the same coefficient estimates as least squares. However, as λ approaches infinity, the shrinkage penalty becomes more influential and the ridge regression coefficient estimates approach zero.

Which predictor variables shrink towards zero the fastest?

In general, the predictor variables that are least influential in the model will shrink towards zero the fastest.

What is the penalty term for ridge regression?

Therefore, ridge regression puts further constraints on the parameters, β j 's, in the linear model. In this case, what we are doing is that instead of just minimizing the residual sum of squares we also have a penalty term on the β 's. This penalty term is λ (a pre-chosen constant) times the squared norm of the β vector. This means that if the β j 's take on large values, the optimization function is penalized. We would prefer to take smaller β j 's, or β j 's that are close to zero to drive the penalty term small.

Which coordinates are shrunk more?

Coordinates with respect to principal components with smaller variance are shrunk more.

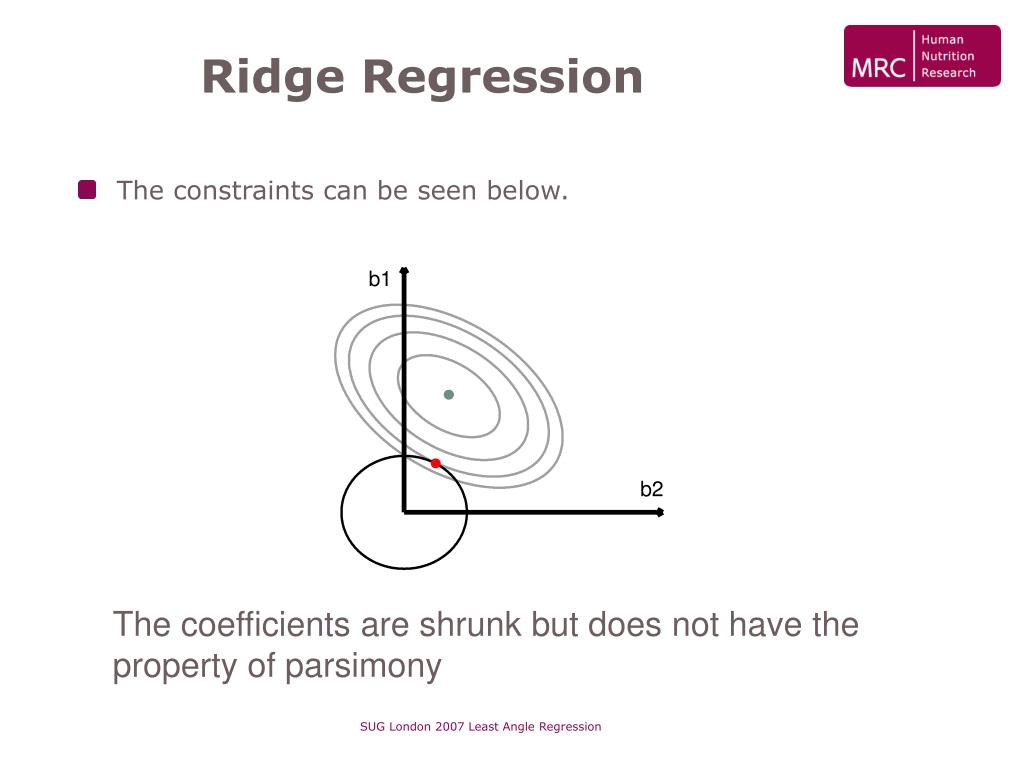
What is the difference between an inner ellipse and an RSS?

The ellipses correspond to the contours of the residual sum of squares (RSS ): the inner ellipse has smaller RSS, and RSS is minimized at ordinal least square (OLS) estimates .

Who proposed that potential instability in the LS estimator?

Hoerl and Kennard (1970) proposed that potential instability in the LS estimator

Is it unusual to see the number of input variables greatly exceed the number of observations?

It is not unusual to see the number of input variables greatly exceed the number of observations, e.g. microarray data analysis, environmental pollution studies.

Does the least square estimator fit well to the test data?

The least square estimator β L S may provide a good fit to the training data, but it will not fit sufficiently well to the test data.

What is ridge regression?

Ridge regression is a term used to refer to a linear regression model whose coefficients are not estimated by ordinary least squares (OLS), but by an estimator , called ridge estimator, that is biased but has lower variance than the OLS estimator.

Which model is Ridge Estimation?

Ridge estimation is carried out on the linear regression model where:

What is the mean squared error of a ridge estimator?

The mean squared error (MSE) of the ridge estimator is equal to the trace of its covariance matrix plus the squared norm of its bias (the so-called bias-variance decomposition):

Which estimator has the lowest variance?

Although, by the Gauss-Markov theorem, the OLS estimator has the lowest variance (and the lowest MSE) among the estimators that are unbiased, there exists a biased estimator (a ridge estimator) whose MSE is lower than that of OLS.

What is ridge estimator?

The ridge estimator solves the slightly modified minimization problem where is a positive constant.

Is the mean squared error of the ridge estimator smaller than the OLS?

In certain cases, the mean squared error of the ridge estimator (which is the sum of its variance and the square of its bias) is smaller than that of the OLS estimator .

Is the ridge estimator unbiased?

We can write the ridge estimator as Therefore, The ridge estimator is unbiased, that is, if and only if But this is possible if only if , that is, if the ridge estimator coincides with the OLS estimator. where is the identity matrix. The bias is